索引優先佇列的工作原理與簡易實現
歡迎探討,如有錯誤敬請指正
1. 優先佇列與索引優先佇列
優先佇列的原理大家應該比較熟悉,本質上就是利用完全二叉樹的結構實現以log2n的時間複雜度刪除佇列中的最小物件(這裡以小堆頂為例)。完全二叉樹又可以通過陣列下標實現索引,當插入一個物件的時候,利用上浮操作更新最小物件。當刪除堆頂最小物件時,將末尾的物件放置到堆頂上,然後執行下沉操作。
優先佇列有一個缺點,就是不能直接訪問已存在於優先佇列中的物件,並更新它們。這個問題在Dijistra演算法中就有明顯的體現,有時候我們需要更新已在佇列中的頂點的距離。為此就需要設計一種新型的資料結構來解決這個問題,這就是本文要介紹的索引優先佇列。
索引優先隊用一個整數和物件進行關聯,當我們需要跟新該物件的值時,可以通這個整數進行快速索引,然後對物件的值進行更新。當然更新後的物件在優先佇列中的位置可能發生變化,這樣以保證整個佇列還是一個優先佇列。
簡易版的索引優先佇列API
|
IndexPriorityQueue<T> |
|
|
IndexPriorityQueue(int capacity, Comparator<T> cmp) |
建構函式,capacity表示佇列容量,cmp表示物件的比較器 |
|
void enqueue(int k, T t) |
將整數k和物件t進行關聯,如果已有和k關聯的物件,則將其更新為t |
|
int dequeue() |
出列,即刪除最物件素並返回與它相關的整數。 |
|
void change(int k, T t) |
將和整數k和關聯的物件更新為t |
注意與物件關聯的整數
2. 索引優先佇列的實現原理
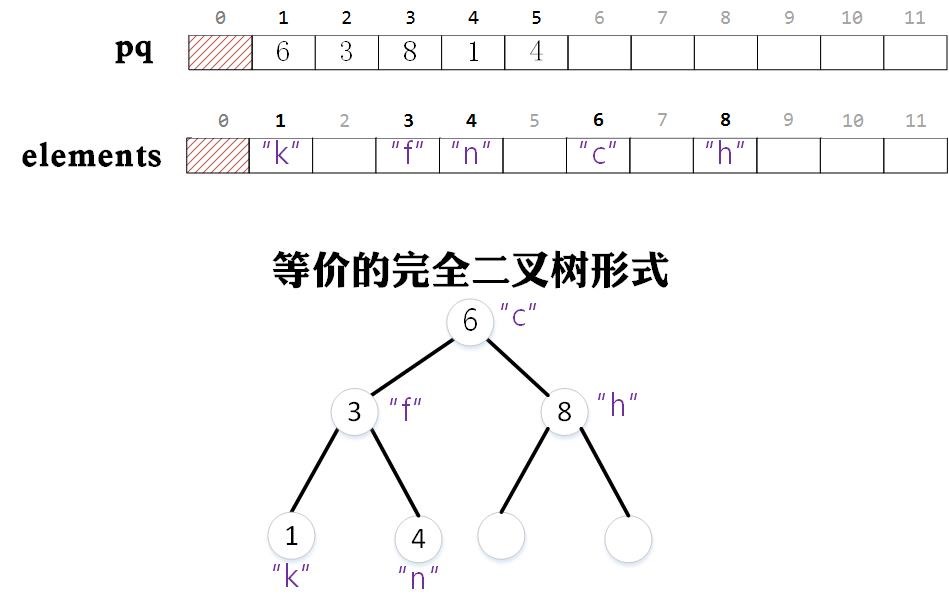
為了實現快速索引,我們首先嚐試一個簡單版本。我們建立兩個陣列分別是pq,elements。elements的作用是儲存物件的引用,我們將每個物件儲存在與之相關的整數作為下標的位置中,elements儲存的物件不一定在陣列中連續存放。pq儲存是與物件相關的整數值,注意陣列pq是連續存放的。此時pq作為優先佇列,但是在上浮和下沉操作中,我們比較的是pq中值作為下標的elements陣列中的值。這樣我們就可以實現快速索引。
下圖中,我們以字串作為儲存的物件型別,建立一個索引優先佇列
從中我們可以看出,我們設計陣列pq陣列的目的。我們只需要對pq中的數值進行維護就可以實現一個優先佇列,而elements中的物件的位置保持不變(出列時會置為null),這樣就可以方便我們快速索引。比如通過elements陣列我們可以知道與整數3相關的字串為“f”。
在圖中,我們插入一個與整數10相關的字串“b”後,pq和elements中的值如下圖所示。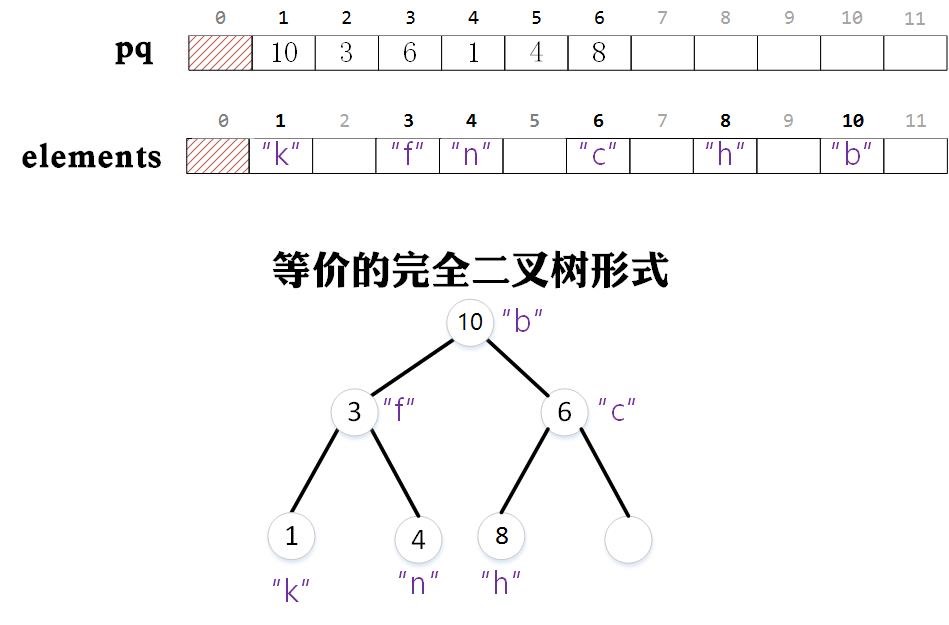
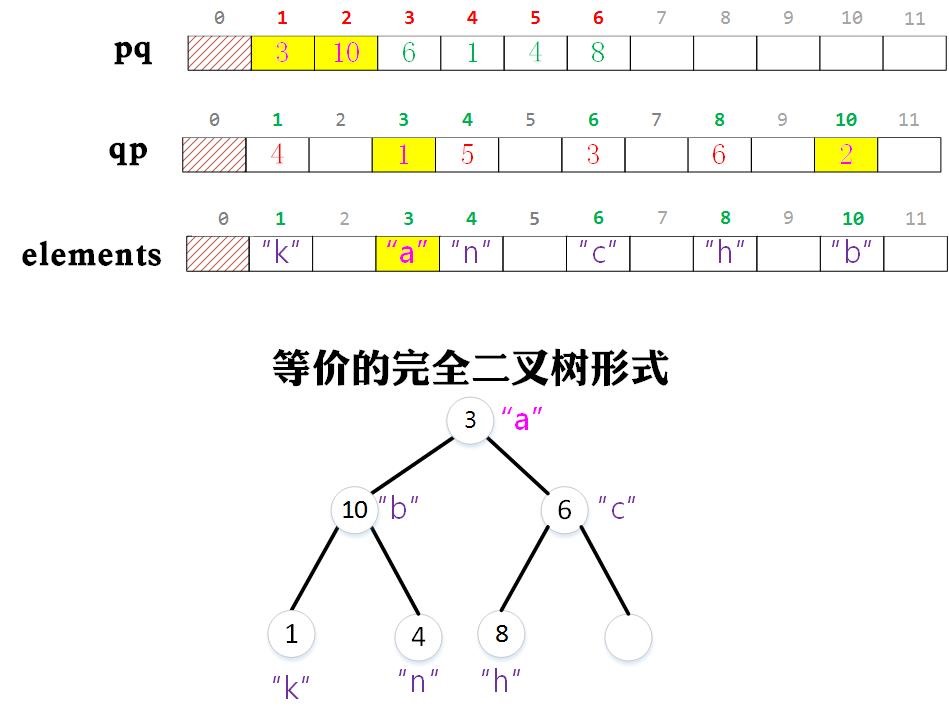
假設在上圖的基礎上,我們要將與整數3相關的字串修改為“a”,那麼我們只需要讓elements[3] = “a”即可。然後去維護pq中的值。但是在維護pq中的值時出現了一個問題,我們不知道pq中哪個位置中的值為3,只能從都到尾遍歷,找到這個元素所在的位置後進行上浮和下沉操作(因為我們必須通過下標才能快速找到父節點或者孩子節點)。為了能夠快速找到pq中元素值對應的下標,我們需要額外設定一個數組qp,它的作用是儲存與物件相關的整數在pq陣列中的下標,並在上浮和下沉的過程中同時維護它。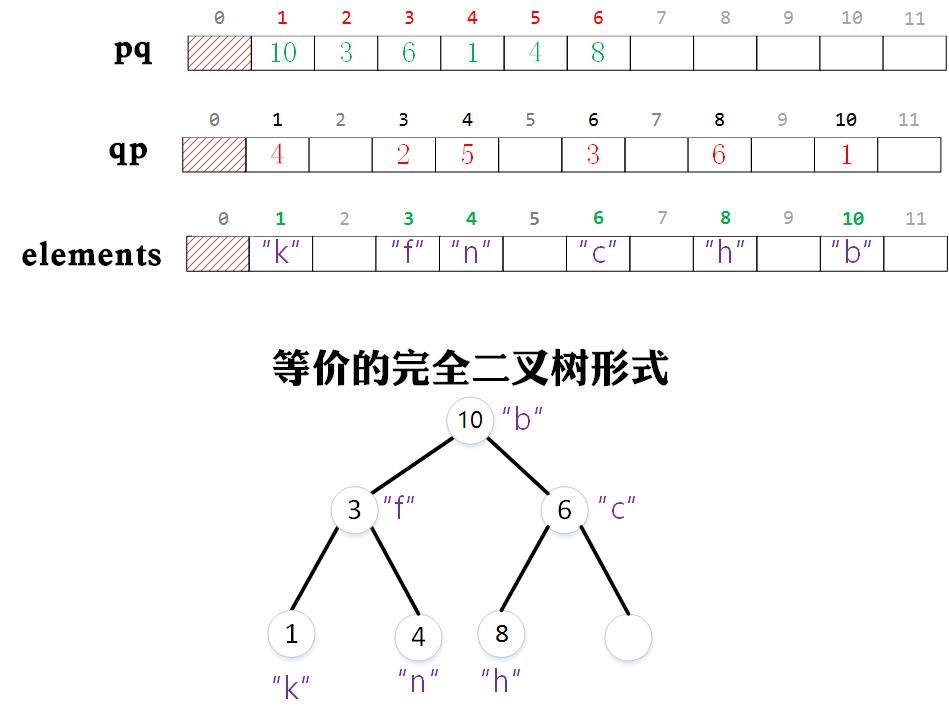
在上述的基礎上,假設我們需要將與整數3相關的字串修改為“a”,那麼我們只需要讓elements[3] = “a”,然後通過qp[3]中的值2就可以知道陣列pq中值為3的下標為2,然後對pq[2]進行上浮或下沉操作。這裡顯然需要進行上浮操作,那麼我們要交換pq[1]和pq[2]的值。這個時候我們需要注意的是,在交換pq陣列中的兩個元素的值時,我們也需要交換qp對應兩個元素的值,因為與物件相關的整數在pq的不同位置上,那麼顯然該整數在pq所在的下標也變了,所以qp中的值也應該發生變化。而需要交換的qp中的兩元素的下標正好就是pq中兩元素的值。結果如下圖所示。所以我們也需要交換qp[3]和qp[10]的值。
3. 索引優先佇列的程式碼實現
上述的索引優先佇列的原理中不能將數字0與物件進行關聯,因為三個陣列沒有使用下標為0的位置。如果要實現與數字0進行關聯,入列時只需要每個關聯的數字加1;當出列時,我們只需要將返回的數字減1。
package datastruct;
import java.util.Arrays;
import java.util.Comparator;
public class IndexPriorityQueue<T> {
private int[] pq;
private int[] qp;
private Object[] element;
private final int capacity;
private int size;
private Comparator<? super T> cmp;
private static class Cmp<T> implements Comparator<T>{
@SuppressWarnings({ "unchecked", "rawtypes" })
@Override
public int compare(T t1, T t2) {
return ((Comparable)(t1)).compareTo(t2);
}
}
private static void swap(int[] a, int i, int j){
int tmp;
tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
//與物件關聯的整數範圍是[0,capacity-1]
public IndexPriorityQueue(int capacity, Comparator<T> cmp){
this.capacity = capacity;
pq = new int[capacity+1];
qp = new int[capacity+1];
Arrays.fill(qp, -1);
element = new Object[capacity+1];
if(cmp == null){
this.cmp = new Cmp<T>();
}
}
public void enqueue(int k, T t){
k++;//使得關聯的整數可以為0
if(k > capacity){
throw new IllegalArgumentException();
}
if(qp[k] != -1){
element[k] = t;
swim(qp[k]);
sink(qp[k]);
return;
}
size++;
pq[size] = k;
qp[k] = size;
element[k] = t;
swim(size);
}
@SuppressWarnings("unchecked")
private void swim(int child){
int parent = child/2;
while(parent > 0){
if(cmp.compare((T)element[pq[child]], (T)element[pq[parent]]) < 0){
swap(pq, child, parent);
swap(qp, pq[child], pq[parent]);
child = parent;
parent = child/2;
}else{
break;
}
}
}
public int dequeue(){
if(size == 0){
throw new IllegalArgumentException();
}
int r = pq[1];
element[r] = null;
swap(pq, size, 1);
swap(qp, pq[size], pq[1]);
pq[size] = -1;
size--;
sink(1);
r--;//使得關聯的整數可以為0
return r;
}
@SuppressWarnings("unchecked")
private void sink(int parent){
int child = parent*2;
while(child <= size){
if(child + 1 <= size){
int r = cmp.compare((T)element[pq[child]], (T)element[pq[child+1]]);
child = r > 0 ? child+1 : child;
}
if(cmp.compare((T)element[pq[child]], (T)element[pq[parent]]) < 0){
swap(pq, parent, child);
swap(qp, pq[parent], pq[child]);
parent = child;
child = parent*2;
}else{
break;
}
}
}
public void change(int k, T t){
k++;
if(qp[k] == -1){
throw new IllegalArgumentException();
}
element[k] = t;
swim(qp[k]);
sink(qp[k]);
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
public static void main(String[] args){
IndexPriorityQueue<String> ipq = new IndexPriorityQueue<String>(11, null);
ipq.enqueue(0, "k");
ipq.enqueue(6, "d");
ipq.enqueue(3, "f");
ipq.enqueue(4, "c");
ipq.enqueue(0, "a");
while(!ipq.isEmpty()){
System.out.println(ipq.dequeue());
}
}
}
4. 參考內容
[1]. 演算法(第4版)Robert Sedgewick 人民郵電出版社