二叉樹的定義與性質，包括各種操作的原始碼在本部落格的的此處：二叉樹

二叉搜尋樹（Binary Search Tree）的定義性質以及原始碼實現在本部落格此處：二叉搜尋樹

平衡二叉樹（AVL樹），是一棵完全二叉樹（PS：關於滿二叉樹與完全二叉樹可以在堆排序中看到定義），其性質以及原始碼的實現在本部落格此處：平衡二叉樹

紅黑樹，是花時間最久理解的一個東西，只理解了其中的原理，其應用最經典的及時本部落格前面講的Apache與Nginx的區別裡面提到的epoll，epoll就是採用紅黑樹的思想實現的，這裡稍微提下紅黑樹用在epoll的什麼地方。

epoll在被核心初始化時（作業系統啟動），同時會開闢出epoll自己的核心高速cache區，用於安置每一個我們想監控的socket，這些socket會以紅黑樹的形式儲存在核心cache裡，以支援快速的查詢、插入、刪除。這個核心高速cache區，就是建立連續的實體記憶體頁，然後在之上建立slab層，簡單的說，就是物理上分配好你想要的size的記憶體物件，每次使用時都是使用空閒的已分配好的物件。

關於紅黑樹的定義及其插入刪除操作在本部落格此處：紅黑樹

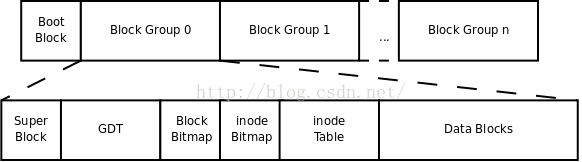
B樹與B+樹，已經不屬於二叉樹的範圍，一個根可以有多個分支，這些主要用在資料庫（如Oracle的資料庫採用B+樹實現）與檔案系統（如ext2，可以看看下圖ext2的佈局）的實現。關於B樹與B+樹的一些理解在本部落格此處：B與B+樹

以上只是眾多樹種的幾種，其實還有經典的最優二叉樹（也就是在資訊理論裡面曾經提到過的霍夫曼編碼，也叫霍夫曼樹）主要用於資料編碼壓縮。

還有B*樹、LSM樹、KD樹、vp、R樹、R*樹、R+樹、X樹、M樹、線段樹、希爾伯特R樹、優先R樹等等眾多的樹。感覺心好累，讓我靜靜先~還是遇到實際的應用場景，需要用啥再研究吧~