AVL平衡二叉樹總結+java實現
目錄
普通二叉搜尋樹的問題
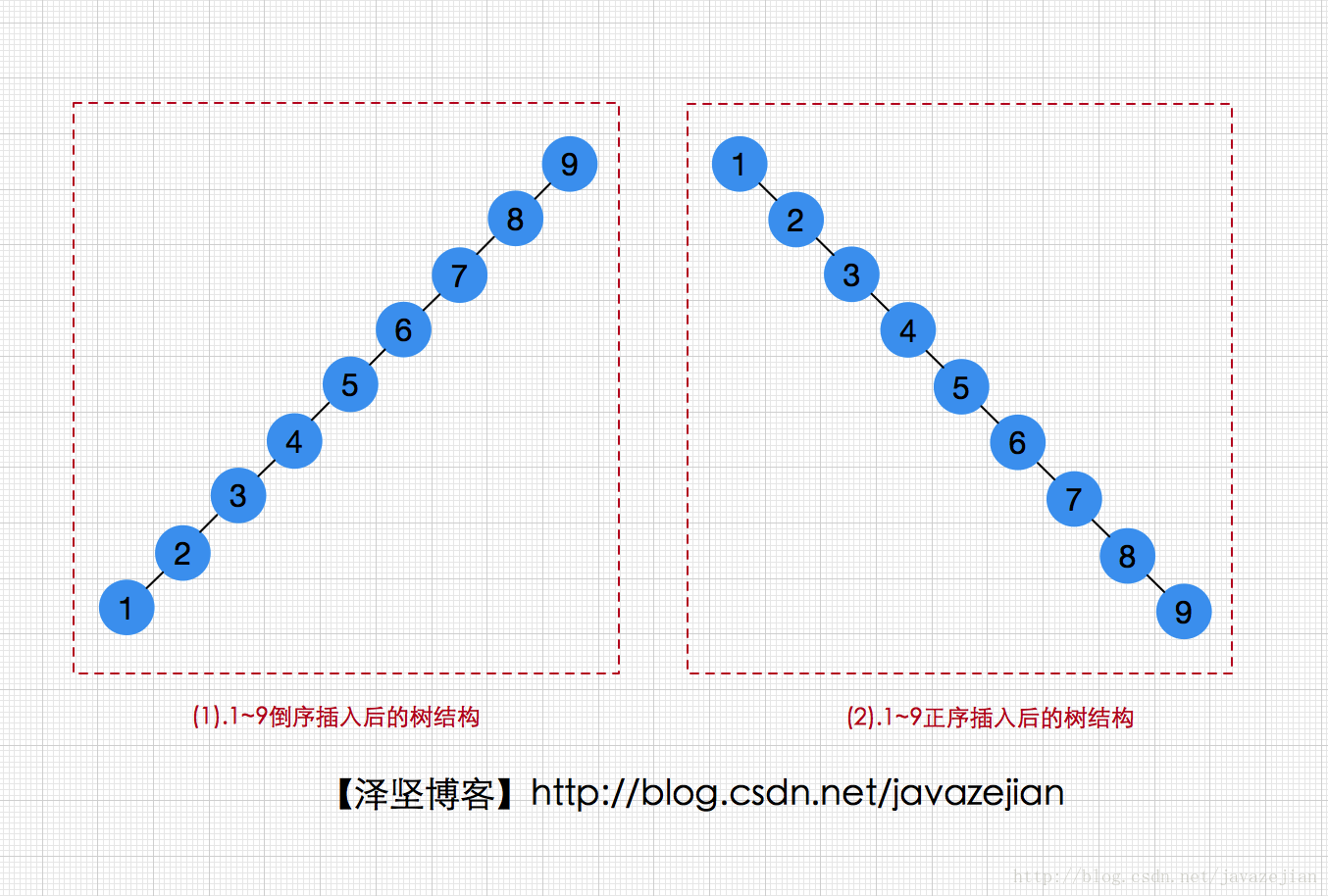
普通二叉樹(二叉查詢樹)在操作的時間複雜度上不一定遵循O(㏒n),也有可能是O(n),這是為什麼呢?在上一篇中,我們明明插入都按照一定規則比較的呀,其實那是因為我們在上篇測試時執行了隨機插入的操作,如果此時利用上篇實現的二叉搜尋樹將一段已排序好的資料一個個插入後,就會發現如下情況了:
從圖中我們可以發現,把已排序的1-9資料進行正序和倒序插入後,樹的結構已變成單向左子樹或者右子樹了,如果我們在往裡插入已排序的資料,那麼單向左子樹或者右子樹越來越長,此時已跟單鏈表沒有什麼區別了,因此對此結構的操作時間複雜度自然就由O(㏒n)變成O(n)了,這也就是普通二叉查詢樹不是嚴格意義上O(㏒n)的原因。那麼該如何解決這個問題呢?事實上一種解決的辦法就是要有一個稱為平衡的附加結構條件即:任何結點的深度不得過深,而這種資料結構就是我們本篇要分析的平衡二叉樹(AVL),它本身也是一種二叉查詢樹,只不過不會出現前面我們分析的情形罷了,接下來我們就來分析一下這棵平衡二叉樹。
AVL樹定義
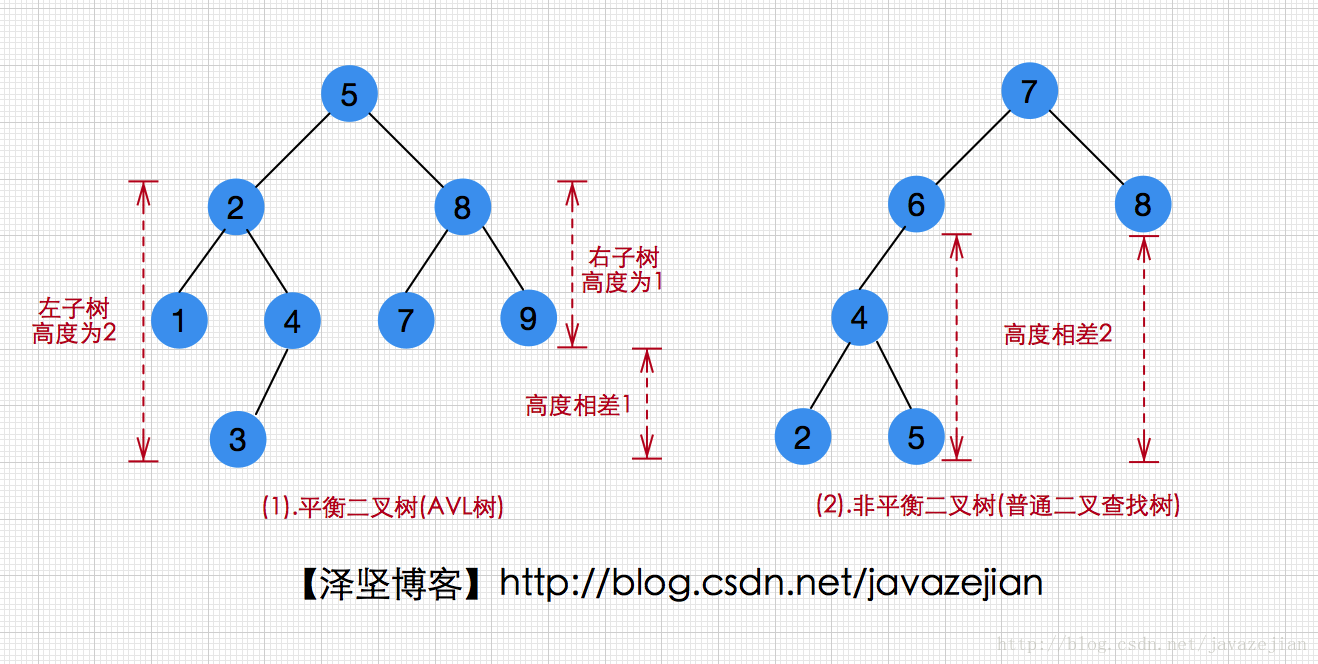
對於一棵BST樹而言,不僅有查詢操作,也有插入、刪除等改變樹的形態的操作。隨著不斷地插入、刪除,BST樹有可能會退化成連結串列的形式,使得查詢的時間複雜度變成O(N),這種情形下,BST樹的結構非常不平衡了。為了保持樹的平衡,需要對樹的形態做一些限制,因此,引入了AVL樹,以保證樹的左右子樹高度之差的絕對值小於等於1。
一棵AVL樹是其每個結點的左子樹和右子樹的高度最多相差1的二叉查詢樹(空樹的高度為-1),這個差值也稱為平衡因子(其取值可以是1,0,-1,平衡因子是某個結點左右子樹層數的差值,有的書上定義是左邊減去右邊,有的書上定義是右邊減去左邊,這樣可能會有正負的區別,但是這個並不影響我們對平衡二叉樹的討論)。如下圖
AVL樹和節點的結構
葉子節點比普通的二叉樹多了一個height,預設值為0,height表達的是這個節點以下的連結數的深度
所以沒有子節點的height=0,有一個子節點為1
public class TreeNode {
int val;
int height=0;//如果這個節點沒有子節點,那麼height=0
public TreeNode left;
public TreeNode right;
public TreeNode(int x) {
val = x;
left=null;
right=null;
}樹裡有一個root
public class AVLBinarySearchTree {
public TreeNode root;
AVL樹高度計算方法
總共4個方法,得到高度2個,計算高度2個
calHeightOne
能夠這個節點的子節點的height都正確,只要重新set這個節點的height
而calHeightAll
不能確定這個節點及以下所有子節點的height,重新set全部子節點的height
//直接返回這個節點的height,防止null的情況的錯誤,null返回-1
public static int getHeight(TreeNode node){
if(node==null){
return -1;
}
return node.height;
}
//返回這個節點左子樹-右子樹的height的差,如果節點為null返回0
//如果為負,則左子樹矮,為正,右子樹矮
public static int getHeightDifference(TreeNode node){
if(node==null){
return 0;
}
return getHeight(node.left)-getHeight(node.right);
}
//不確定這個節點及以下所有子節點的height,重新set他們的height
//此處的height表達的是這個節點以下的連結數的深度
//所以沒有子節點為(-1+1)=0,有一個子節點為max(-1,0)+1=1
public static int calHeightAll(TreeNode node){
if(node==null){
return -1;
}
int nowHeight=Math.max(calHeightAll(node.left), calHeightAll(node.right))+1;
node.height=nowHeight;
return nowHeight;
}
//確定這個節點的子節點的height,重新set這個節點的height
public static int calHeightOne(TreeNode node){
if(node==null){
return -1;
}
int nowHeight=Math.max(getHeight(node.left), getHeight(node.right))+1;
node.height=nowHeight;
return nowHeight;
}AVL樹旋轉
在每一次插入數值之後,樹的平衡性都可能被破壞,這時可以通過一個簡單的操作來矯正平衡–旋轉。
旋轉的目的就是減少高度,通過降低整棵樹的高度來平衡。哪邊的樹高,就把那邊的樹向上旋轉。
通過旋轉可以降低高度。
所謂的左旋和右旋都是以子樹為原點的:如b是a的子樹,那麼旋轉就圍繞b來進行。
如果b是a的左子樹,那麼就圍繞b將a向右旋轉,看著就像是a直接掉下來了,掉成了b的右子樹。
如果b是a的右子樹,那麼就圍繞b將a向左旋轉,看著就像是a直接掉下來了,掉成了b的左子樹。
插入節點時分四種情況,四種情況對應的旋轉方法是不同的:
例如對於被破壞平衡的節點 a 來說:
注意插入方式LL是指在左子樹的左子樹插入節點,而不是左旋轉。
| 插入方式 | 描述 | 旋轉方式 |
| LL | 在a的左子樹根節點的左子樹上插入節點而破壞平衡 | 右旋轉 |
| RR | 在a的右子樹根節點的右子樹上插入節點而破壞平衡 | 左旋轉 |
| LR | 在a的左子樹根節點的右子樹上插入節點而破壞平衡 | 先左旋後右旋 |
| RL | 在a的右子樹根節點的左子樹上插入節點而破壞平衡 | 先右旋後左旋 |
LL 右旋轉
就拿最簡單的舉例了。
一個簡單的AVL樹:
這時是平衡的,如果在插入一個元素3,就會變成下面這樣,破壞平衡:
被破壞了平衡首先要找到是哪個樹被破壞了平衡,然後調整這個樹。然後繼續往上一個一個的調整。
既然是被新插入的節點3破壞的,那麼不平衡的樹一定在從新插入的節點3到根節點8的路徑上。找離新插入的節點最近的不平衡的樹進行調整,上圖中就是7.
節點7的左子樹 高度為1,右子樹為空,高度為-1 ,不平衡。根據表格要進行右旋轉。
先把7這顆不平衡的樹挑出來:
這棵樹是最近的不平衡的樹,7的左子樹5高度為1,右子樹為空,所以右子樹高度是-1.兩者的高度差達到了2,超過了1.
因為左子樹5的高度更高,所以要把左子樹5向上提一下,這時旋轉就很明顯了,抓著5向上一提,7就掉到5的右邊了,成了5的右子樹。
這個過程就是右旋:
這時繼續往上找,發現每個節點都符合了平衡條件,所以整棵樹就變成了AVL樹。
那如果節點5本來就有了右子樹呢?照樣右旋轉,只要把原來5的右子樹變成旋轉後的7的左子樹就行了。因為5的右子樹肯定比5大,但是也肯定比7小的:
其實上面最後旋轉成的樹是下面這樣的:
這棵樹的根節點是不平衡的,還需要使用後面的雙旋轉來調整。
演算法 rotateRight(nodeN)
nodeL = nodeN 的左孩子
將nodeN 的左孩子置為 nodeL 的右孩子
將 nodeL 的右孩子置為 nodeN
return nodeL //右旋轉
public TreeNode rotateRight(TreeNode node){
TreeNode leftNode=node.left;
node.left=leftNode.right;
leftNode.right=node;
return leftNode;
}
RR 左旋轉
在右子樹的右子樹上插入節點破壞的平衡需要左旋轉來矯正。
左旋轉和右旋轉類似,都是單旋轉,給個流程圖。
演算法 rotateLeft(nodeN)
nodeR = nodeN 的右孩子
將 nodeN 的右孩子置為 nodeR 的左孩子
將 nodeR 的左孩子置為 nodeN
return nodeR //左旋轉 返回選擇後的根節點
public TreeNode rotateLeft(TreeNode node){
TreeNode rightNode=node.right;
node.right=rightNode.left;
rightNode.left=node;
return rightNode;
}
LR 左旋右旋
如果在第一個例子中插入的不是3,而是6,就成了下面的樣子,依然說破壞了平衡
被破壞平衡的樹依然是7,但是這次就不能通過一次旋轉解決了,咋轉都不行。
要從6開始到7進行先左旋再右旋才可以矯正平衡:
進行左-右旋轉,即先對結點N的孫子進行左旋轉,再對結點N的新孩子進行右旋轉,演算法如下:
演算法 rotateLeftRight(nodeN)
nodeL = nodeN 的左孩子
將 nodeN 的左孩子置為由 rotateLeft(nodeN 孩子的孩子)返回的結點
return rotateLeft(nodeN 新的左孩子) //左旋轉 然後右旋轉
public TreeNode rotateLeftAndRight(TreeNode node){
TreeNode leftNode=node.left;
node.left=rotateLeft(leftNode);
return rotateRight(node);
}RL 右旋左旋
當破壞平衡的節點是這個樹的右子樹的左子樹時,要進行先右旋轉再左旋轉來矯正。
同樣是從破壞平衡的那個節點開始旋轉,先右旋轉後左旋轉:
進行右-左旋轉,即先對結點N 的孫子(孩子的孩子,"位於新插入元素的那個方向")進行右旋轉;再對結點N 的新孩子進行左旋轉,演算法如下:
演算法 rotateRightLeft(nodeN)
nodeR = nodeN 的右孩子
將 nodeN 的右孩子置為由 rotateRight(nodeN 的孩子的孩子)返回的結點
return rotateLeft(nodeN 的新的右孩子) //右旋轉 然後左旋轉
public TreeNode rotateRightAndLeft(TreeNode node){
TreeNode rightNode=node.right;
node.right=rotateRight(rightNode);
return rotateLeft(node);
}平衡節點
可以根據節點的左右節點的高度差確定旋轉方式,具體可以看旋轉的那個表格
注意:
如果做了旋轉,則對node重新進行height的計算,node及node的子節點的height是正確的,讓node的上一層只需做calNodeOne的計算就行
//平衡這個node,進行旋轉,返回根節點
//如果做了旋轉,則對node重新進行height的計算,讓node的上一層只需做calNodeOne的計算就行
//node的height已經計算正確
public TreeNode rebalanceNode(TreeNode node){
int difference=getHeightDifference(node);
//左子樹高
if(difference>1){
if(getHeightDifference(node.left)>0){
node=rotateRight(node);
}
else{
node=rotateLeftAndRight(node);
}
calHeightAll(node);
}
//右子樹高
if(difference<-1){
if(getHeightDifference(node.right)<0){
node=rotateLeft(node);
}
else{
node=rotateRightAndLeft(node);
}
calHeightAll(node);
}
return node;
}插入節點
用遞迴的方法,返回節點,讓left或right=返回後的節點
//插入節點,如果已存在相同的樹,則不插入,
public void insertNode(int x){
if(root==null){
root=new TreeNode(x);
calHeightOne(root);
}
root=insertNode(root,x);
root=rebalanceNode(root);
}
public TreeNode insertNode(TreeNode node,int x){
//如果為空,返回新節點x
if(node==null){
return new TreeNode(x);
}
int now=node.val;
//如果相等,不插入,直接返回
if(now==x){
return node;
}
if(now>x){
node.left=insertNode(node.left, x);
node.left=rebalanceNode(node.left);
calHeightOne(node);
}
else{
node.right=insertNode(node.right, x);
node.right=rebalanceNode(node.right);
calHeightOne(node);
}
return node;
}
刪除節點
刪除節點需要查詢一個節點下的max和min節點的方法
查詢最大最小節點
//返回這個node下max的子節點,就是最右的子節點
public TreeNode findMaxNode(TreeNode node){
if(node==null){
return null;
}
while(node.right!=null){
node=node.right;
}
return node;
}
//返回這個node下min的子節點,就是最左的子節點
public TreeNode findMinNode(TreeNode node){
if(node==null){
return null;
}
while(node.left!=null){
node=node.left;
}
return node;
}刪除
如果刪除的那個節點左右子樹有一個為空,則把下面的接到上面去
如果都不為空
如果tree的左子樹比右子樹高; 則找出tree的左子樹中的最大節點 將該最大節點的值賦值給tree。 刪除該最大節點。 這類似於用"tree的左子樹中最大節點"做"tree"的替身; 採用這種方式的好處是:刪除"tree的左子樹中最大節點"之後,AVL樹仍然是平衡的。
反之亦然
//如果樹中沒有值為x,則啥都不幹,否則刪除這個節點
public void deleteNode(int x){
if(root==null){
return;
}
root=deleteNode(root,x);
root=rebalanceNode(root);
calHeightOne(root);
}
public TreeNode deleteNode(TreeNode node,int x){
//如果為空,返回新節點x
if(node==null){
return null;
}
int now=node.val;
if(now>x){
node.left=deleteNode(node.left, x);
node.left=rebalanceNode(node.left);
calHeightOne(node);
}
if(now<x){
node.right=deleteNode(node.right, x);
node.right=rebalanceNode(node.right);
calHeightOne(node);
}
//如果相等,
if(now==x){
if(node.left!=null&&node.right!=null){
int difference=getHeightDifference(node);
//如果左子樹比右子樹高,用左子樹的max替代node,node的平衡不會被 破壞
if(difference>0){
TreeNode max=findMaxNode(node.left);
int maxValue=max.val;
node.val=maxValue;
node.left=deleteNode(node.left, maxValue);
}
//如果左子樹比右子樹矮或者相同,用右子樹的min替代node,node的平衡不會被 破壞
else{
TreeNode min=findMinNode(node.right);
int minValue=min.val;
node.val=minValue;
node.right=deleteNode(node.right, minValue);
}
}
//左右子樹至少一個為空
else{
if(node.left!=null){
node=node.left;
}
else{
node=node.right;
}
}
}
return node;
}完整程式碼
主程式
package datastructure.tree.avlbinarysearchtree;
public class Main {
public static void main(String[] args) {
int[] x=new int[]{3,2,1,4,5,6,7};
AVLBinarySearchTree tree=new AVLBinarySearchTree(x);
//tree.insertNode(3);
AVLBinarySearchTree.calHeightAll(tree.root);
AVLBinarySearchTree.printTree(tree.root);
//BinarySearchTree.inOrder(tree.root);
//BinarySearchTree.breadthFirstSearch(tree.root);
//BinarySearchTree.depthFirstSearch(tree.root);
//tree.root=tree.rotateRightAndLeft(tree.root);
//TreeNode now=tree.findNode(2);
//now.printTree(now);
tree.deleteNode(4);
AVLBinarySearchTree.calHeightAll(tree.root);
AVLBinarySearchTree.printTree(tree.root);
}
}
葉節點
package datastructure.tree.avlbinarysearchtree;
import java.util.LinkedList;
import java.util.Queue;
public class TreeNode {
int val;
int height=0;//如果這個節點沒有子節點,那麼height=0
public TreeNode left;
public TreeNode right;
public TreeNode(int x) {
val = x;
left=null;
right=null;
}
//通過佇列 當前下層節點個數 列印每層的節點和null,為了方便列印
public static void printTree(TreeNode root){
if(root == null)
return;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
int current;//當前層 還未列印的結點個數
int next;//下一層結點個數
queue.offer(root);
current = 1;
next = 0;
while(!queue.isEmpty()){
TreeNode currentNode = queue.poll();
if (currentNode!=null) {
System.out.print(currentNode.val+" ");
current--;
}
else{
System.out.print("null ");
current--;
queue.offer(null);
next++;
queue.offer(null);
next++;
if(current ==0){
System.out.println();
current = next;
next = 0;
int temp=0;
for (TreeNode treeNode : queue) {
if(treeNode==null){
temp++;
}
}
if(temp==current){
System.out.println("end");
break;
}
}
continue;
}
if(currentNode.left != null){
queue.offer(currentNode.left);
next++;
}
else{
queue.offer(null);
next++;
}
if(currentNode.right != null){
queue.offer(currentNode.right);
next++;
}
else{
queue.offer(null);
next++;
}
if(current ==0){
System.out.println();
current = next;
next = 0;
int temp=0;
for (TreeNode treeNode : queue) {
if(treeNode==null){
temp++;
}
}
if(temp==current){
System.out.println("end");
break;
}
}
}
}
}
avl樹
package datastructure.tree.avlbinarysearchtree;
import java.nio.channels.NetworkChannel;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
public class AVLBinarySearchTree {
public TreeNode root;
//只有一個int,則root為x的節點
public AVLBinarySearchTree(int x){
root=new TreeNode(x);
}
//x為陣列,如果長度為0,初始化root為0的節點
//否則逐個插入x的元素
public AVLBinarySearchTree(int[] x){
int length=x.length;
for(int i=0;i<length;i++){
insertNode(x[i]);
}
}
//直接返回這個節點的height,防止null的情況的錯誤,null返回-1
public static int getHeight(TreeNode node){
if(node==null){
return -1;
}
return node.height;
}
//返回這個節點左子樹-右子樹的height的差,如果節點為null返回0
//如果為負,則左子樹矮,為正,右子樹矮
public static int getHeightDifference(TreeNode node){
if(node==null){
return 0;
}
return getHeight(node.left)-getHeight(node.right);
}
//不確定這個節點及以下所有子節點的height,重新set他們的height
//此處的height表達的是這個節點以下的連結數的深度
//所以沒有子節點為(-1+1)=0,有一個子節點為max(-1,0)+1=1
public static int calHeightAll(TreeNode node){
if(node==null){
return -1;
}
int nowHeight=Math.max(calHeightAll(node.left), calHeightAll(node.right))+1;
node.height=nowHeight;
return nowHeight;
}
//確定這個節點的子節點的height,重新set這個節點的height
public static int calHeightOne(TreeNode node){
if(node==null){
return -1;
}
int nowHeight=Math.max(getHeight(node.left), getHeight(node.right))+1;
node.height=nowHeight;
return nowHeight;
}
//左旋轉 返回選擇後的根節點
public TreeNode rotateLeft(TreeNode node){
TreeNode rightNode=node.right;
node.right=rightNode.left;
rightNode.left=node;
return rightNode;
}
//右旋轉
public TreeNode rotateRight(TreeNode node){
TreeNode leftNode=node.left;
node.left=leftNode.right;
leftNode.right=node;
return leftNode;
}
//左旋轉 然後右旋轉
public TreeNode rotateLeftAndRight(TreeNode node){
TreeNode leftNode=node.left;
node.left=rotateLeft(leftNode);
return rotateRight(node);
}
//右旋轉 然後左旋轉
public TreeNode rotateRightAndLeft(TreeNode node){
TreeNode rightNode=node.right;
node.right=rotateRight(rightNode);
return rotateLeft(node);
}
//平衡這個node,進行旋轉,返回根節點
//如果做了旋轉,則對node重新進行height的計算,讓node的上一層只需做calNodeOne的計算就行
//node的height已經計算正確
public TreeNode rebalanceNode(TreeNode node){
int difference=getHeightDifference(node);
//左子樹高
if(difference>1){
if(getHeightDifference(node.left)>0){
node=rotateRight(node);
}
else{
node=rotateLeftAndRight(node);
}
calHeightAll(node);
}
//右子樹高
if(difference<-1){
if(getHeightDifference(node.right)<0){
node=rotateLeft(node);
}
else{
node=rotateRightAndLeft(node);
}
calHeightAll(node);
}
return node;
}
//插入節點,如果已存在相同的樹,則不插入,
public void insertNode(int x){
if(root==null){
root=new TreeNode(x);
calHeightOne(root);
}
root=insertNode(root,x);
root=rebalanceNode(root);
}
public TreeNode insertNode(TreeNode node,int x){
//如果為空,返回新節點x
if(node==null){
return new TreeNode(x);
}
int now=node.val;
//如果相等,不插入,直接返回
if(now==x){
return node;
}
if(now>x){
node.left=insertNode(node.left, x);
node.left=rebalanceNode(node.left);
calHeightOne(node);
}
else{
node.right=insertNode(node.right, x);
node.right=rebalanceNode(node.right);
calHeightOne(node);
}
return node;
}
//根據int x查詢二叉搜尋樹的節點,如果沒找到 返回null,找到了,返回該節點
//now=root 進入true的迴圈 如果now=null,說明沒有返回null,now的值=x,說明找到,返回now
//否則根據now與x的大小,now=now的左右子節點
public TreeNode findNode(int x){
if(root==null){
return null;
}
TreeNode now=root;
while(true){
if(now==null){
return null;
}
if(now.val==x){
return now;
}
if(now.val<x){
now=now.right;
}
else {
now=now.left;
}
}
}
//返回這個node下max的子節點,就是最右的子節點
public TreeNode findMaxNode(TreeNode node){
if(node==null){
return null;
}
while(node.right!=null){
node=node.right;
}
return node;
}
//返回這個node下min的子節點,就是最左的子節點
public TreeNode findMinNode(TreeNode node){
if(node==null){
return null;
}
while(node.left!=null){
node=node.left;
}
return node;
}
//如果樹中沒有值為x,則啥都不幹,否則刪除這個節點
public void deleteNode(int x){
if(root==null){
return;
}
root=deleteNode(root,x);
root=rebalanceNode(root);
calHeightOne(root);
}
public TreeNode deleteNode(TreeNode node,int x){
//如果為空,返回新節點x
if(node==null){
return null;
}
int now=node.val;
if(now>x){
node.left=deleteNode(node.left, x);
node.left=rebalanceNode(node.left);
calHeightOne(node);
}
if(now<x){
node.right=deleteNode(node.right, x);
node.right=rebalanceNode(node.right);
calHeightOne(node);
}
//如果相等,
if(now==x){
if(node.left!=null&&node.right!=null){
int difference=getHeightDifference(node);
//如果左子樹比右子樹高,用左子樹的max替代node,node的平衡不會被 破壞
if(difference>0){
TreeNode max=findMaxNode(node.left);
int maxValue=max.val;
node.val=maxValue;
node.left=deleteNode(node.left, maxValue);
}
//如果左子樹比右子樹矮或者相同,用右子樹的min替代node,node的平衡不會被 破壞
else{
TreeNode min=findMinNode(node.right);
int minValue=min.val;
node.val=minValue;
node.right=deleteNode(node.right, minValue);
}
}
//左右子樹至少一個為空
else{
if(node.left!=null){
node=node.left;
}
else{
node=node.right;
}
}
}
return node;
}
//遞迴
public static void preOrder(TreeNode root){
if(root==null){
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}
public static void inOrder(TreeNode root){
if(root==null){
return;
}
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}
public static void postOrder(TreeNode root){
if(root==null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+" ");
}
//通過佇列 當前下層節點個數 列印每層的節點和null
public static void printTree(TreeNode root){
if(root == null)
return;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
int current;//當前層 還未列印的結點個數
int next;//下一層結點個數
queue.offer(root);
current = 1;
next = 0;
while(!queue.isEmpty()){
TreeNode currentNode = queue.poll();
if (currentNode!=null) {
//System.out.print(currentNode.val+" ");
System.out.print(currentNode.val+
"(h="+currentNode.height+")"+
"(d="+getHeightDifference(currentNode)+") ");
current--;
}
else{
System.out.print("null ");
current--;
queue.offer(null);
next++;
queue.offer(null);
next++;
if(current ==0){
System.out.println();
current = next;
next = 0;
int temp=0;
for (TreeNode treeNode : queue) {
if(treeNode==null){
temp++;
}
}
if(temp==current){
System.out.println("end");
break;
}
}
continue;
}
if(currentNode.left != null){
queue.offer(currentNode.left);
next++;
}
else{
queue.offer(null);
next++;
}
if(currentNode.right != null){
queue.offer(currentNode.right);
next++;
}
else{
queue.offer(null);
next++;
}
if(current ==0){
System.out.println();
current = next;
next = 0;
int temp=0;
for (TreeNode treeNode : queue) {
if(treeNode==null){
temp++;
}
}
if(temp==current){
System.out.println("end");
break;
}
}
}
}
//寬度優先遍歷 是簡化的按層遍歷,沒有了current和next和列印null
public static void breadthFirstSearch(TreeNode root){
Queue<TreeNode> queue = new LinkedList<TreeNode>();
if(root==null){
return;
}
queue.offer(root);
while(!queue.isEmpty()){
TreeNode now=queue.poll();
System.out.print(now.val+" ");
if(now.left!=null){
queue.offer(now.left);
}
if(now.right!=null){
queue.offer(now.right);
}
}
System.out.println();
}
//深度優先遍歷
//用棧 彈出自身 先加入右節點 再加入左節點,這樣先彈出左節點,左節點的左右子節點又塞進去,在原右節點上面
public static void depthFirstSearch(TreeNode root){
Stack<TreeNode> stack=new Stack<TreeNode>();
if(root==null){
return;
}
stack.push(root);
while(!stack.isEmpty()){
TreeNode now=stack.pop();
System.out.print(now.val+" ");
if(now.right!=null){
stack.push(now.right);
}
if(now.left!=null){
stack.push(now.left);
}
}
System.out.println();
}
}