這個問題從高中就開始疑惑，計算機究竟是如何理解人類思維，如何進行計算？我很想知道最最基本的工作原理，但是大學裡好多課程，數字邏輯，計算機組成原理，只是從不同層次上解釋了計算機的工作原理，很可惜的是，我並沒有把知識穿起來。看了很多人的回答，大家也只是解釋了一部分問題，沒有完整的把計算機整個的抽象層次說清楚。在大學裡我看到了 Charles Petzold的《編碼 隱匿在計算機軟硬體背後的語言》，這部永不退色的計算機經典著作，為了講明白了這件事兒，今天我決定用自己簡略的話，回顧一下作者寫作的思路，用我的理解為大家講述計算機的工作原理。希望我能夠完成。

今天的計算機已經變得相當複雜，是有史以來人類創造的最複雜最精密的儀器，沒有之一，是二十世紀技術領域的“登峰造極之作”，計算機與生俱來的層次化體系結構，掩蓋了技術背後最本質的東西，現在已經很少有人去關心計算機最本質的工作原理，我希望能剖析計算機一層層‘“抽象”面紗，展現最本質的“計算”過程。基本的知識基礎是高中物理，高中數學。

第一節 計算器

下面回到高中課堂，我依稀記得在電磁學那一部分，講到了電磁繼電器，當時老師說，繼電器是很重要的發明，我開啟物理課本，“什麼破東西嘛”，太簡單了，那時候覺得像繼電器這樣的發明沒什麼用。高中數學中也講到，布林代數，簡單老說就是，與、或、非，而且教科書上說，布林代數意義重大云云。下面問題來了，我只用繼電器能不是實現簡單的計算器？注意是“計算器”，而不是計算機，答案是肯定的，來，那就看看，如何用繼電器打造出一個”計算器“，進而打造出一臺”計算機“

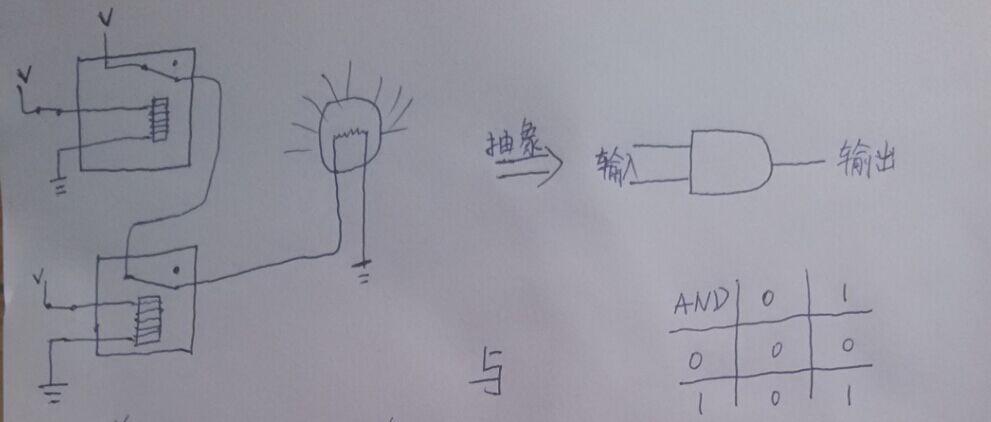
兩個繼電器串聯，點亮一盞燈，這算不算實現了“與”的操作呢？兩“真”為”真“

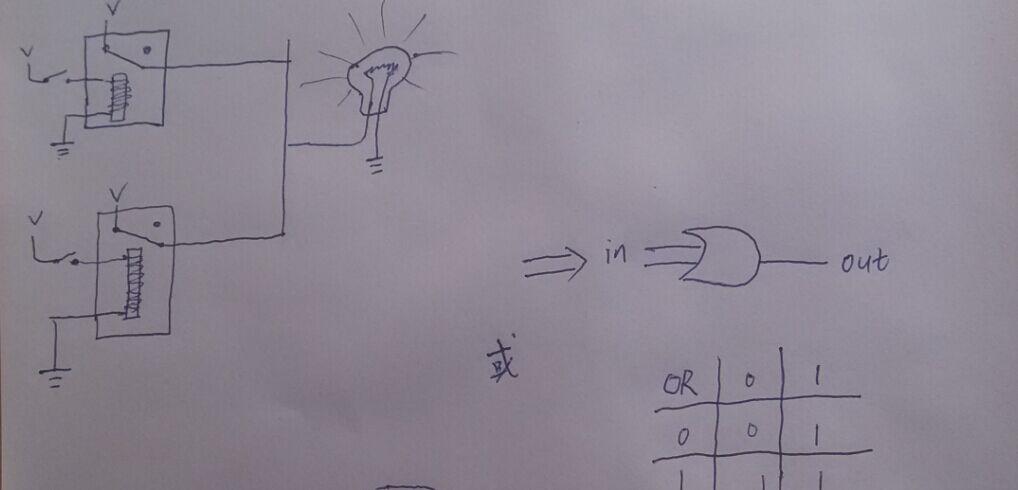
兩個繼電器並聯，點亮一盞燈，是不是實現了”或“的操作？一真為真

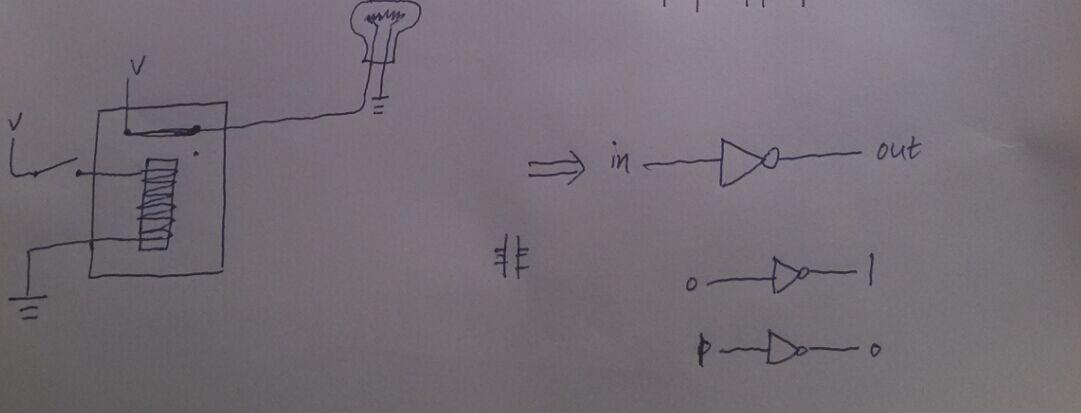
一個繼電器本身就可以實現”非“的操作

這樣一來，物理上的繼電器，和布林代數，完美的融合起來，我把與或非門繼電器實現稱作”物理層“，每張圖右邊的符號表示，稱作”布林邏輯層“，從”物理層“到”布林邏輯層“是我們的第一層抽象，很簡單吧？（當然現代計算器從物理實現到邏輯實現，已經不再使用繼電器，而是在矽晶片上雕刻一個個的電晶體，但電晶體的數量絕對不會減少，這一點@丁旭 已經說得很明白）

接下來可能有人問，你整這些小兒科的東西，有什麼用呢？別急，看我慢慢展開！

我們知道，布林代數是一種數學，既然是在一種數學，那麼存在數學運算啊，數學運算能用繼電器實現嗎，of course

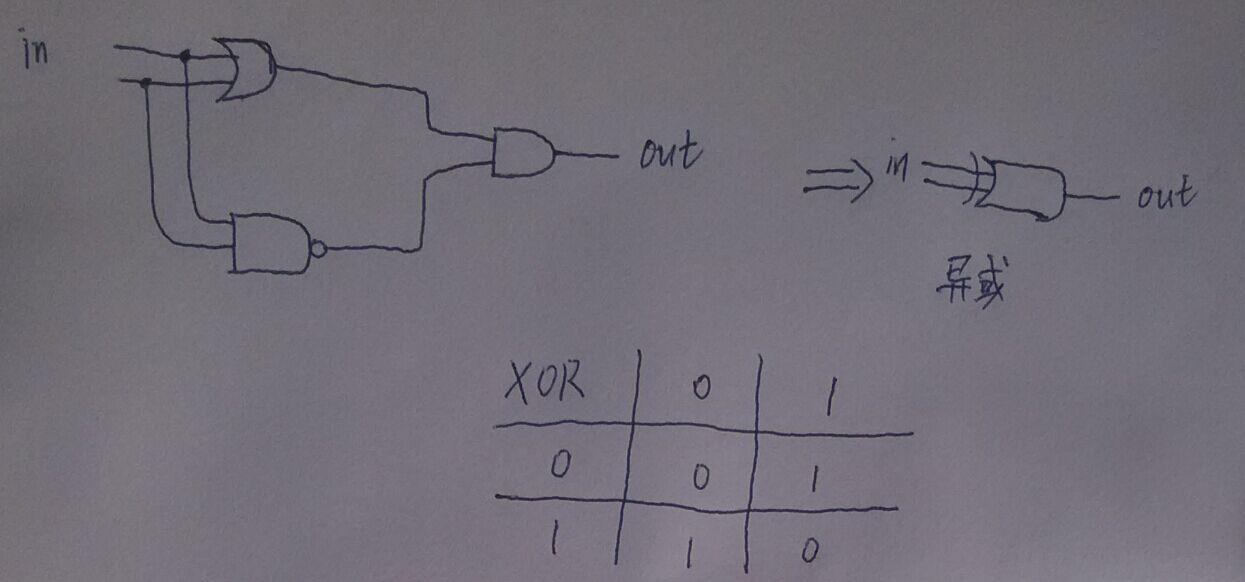
一個或門，一個與非門，一個與門，按照圖示連在一起形成了一個最常見的運算，異或運算，”相同為假，不同為真“，那物理實現上怎麼做呢？請在大腦中想想怎麼連線，一共七個繼電器就可以實現，有了異或運算，我們就可以實現更復雜的運算，下面就和我們實現一臺”計算器“直接相關了

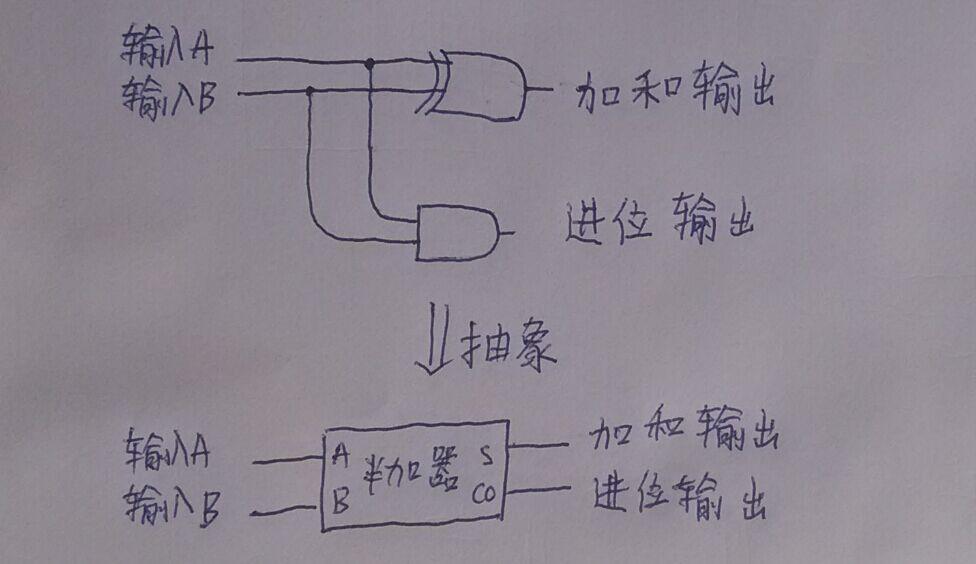
一個異或門和一個與門，形成一個”半加器“，圖示下邊的符號表示一個半加器，這裡是新一層的抽象，從布林邏輯運算到”計算器件“的抽象

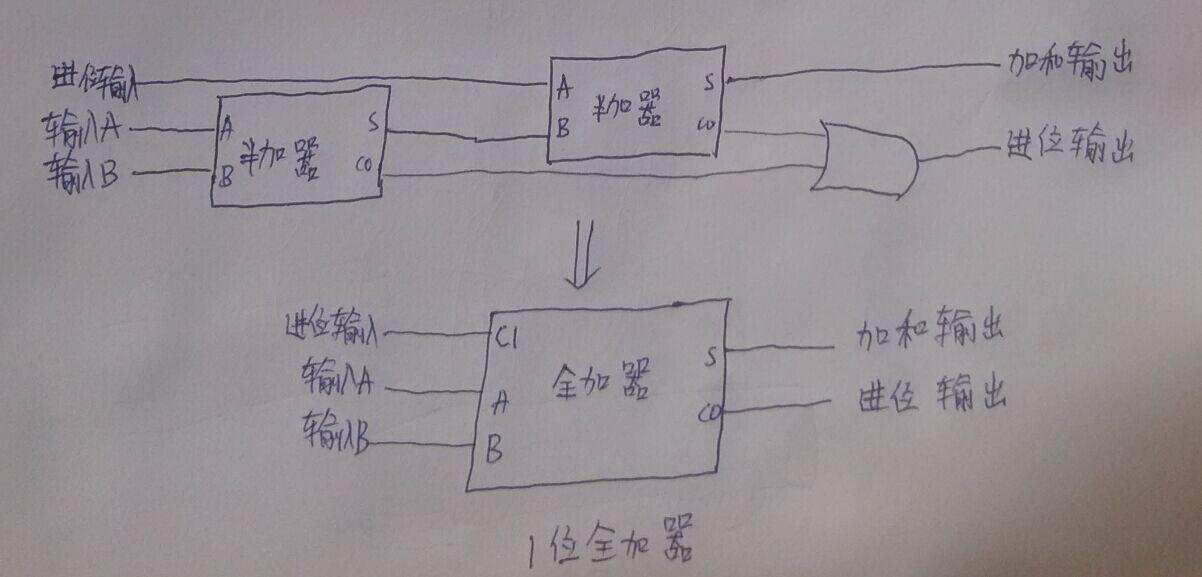
有一個半加器，距離我們實現手工打造一個”計算機“還很遠，然而兩個半加器，一個或門，可以實現一個”全加器“，為什麼叫全加器呢？因為我們使用它可以實現一位加法的計算！（這裡是二進位制，問題的題目，為什麼計算機能讀懂”0“和”1“，看到這裡是不是心頭一喜呢？）

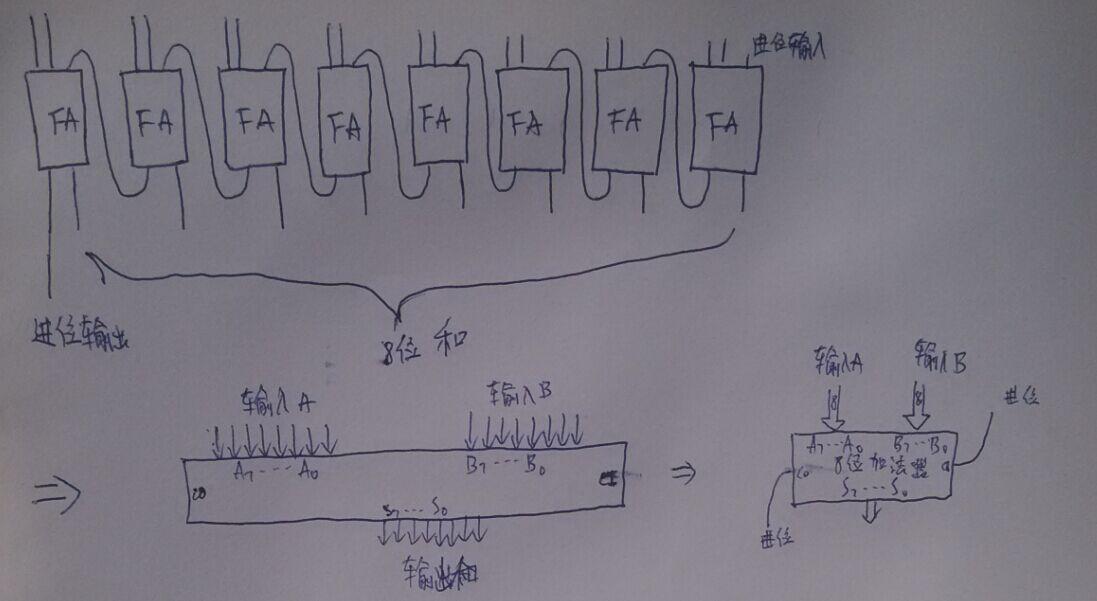
有了一位”全加器“，我們實現8位加法的計算還遠嗎？當然不遠，8個全加器，按圖示相連，就可以實現8位加法計算（和我們在紙上進行加法運算很像，進位的操作很顯然。當然，這裡都是進行二進位制加法），右下方是8位加法器的表示方式。

要是這會兒在19世紀，在電力革命的年代，我一定要親手打造一個計算器！

畫的比較簡陋，見過卡車上的按鈕嗎？上下撥動的那種，這是我穿越回19世紀站在專利局門口，闡述我”偉大”的發明，“我發明的計算器，有兩排輸入按鈕，每個按鈕上下撥動表示輸入的是0或者1，最下排是9個燈泡，燈泡的亮與滅，指示這一位是0，還是1，我的發明是劃時代的，可以把人類從繁雜的計算過程中解救出來...”

“什麼？就因為我的計算器不能實現減法運算兒拒絕我的專利申請，減法運算？減法運算，怎樣實現計算機的減法運算呢？”

計算機發展過程中，最重要的思想是“抽象”，一層層的抽象封裝了實現的細節，使的計算機開發人員更關注與邏輯的實現，相信有了我上面的表述，讀者應該能看懂下邊的抽象思想：

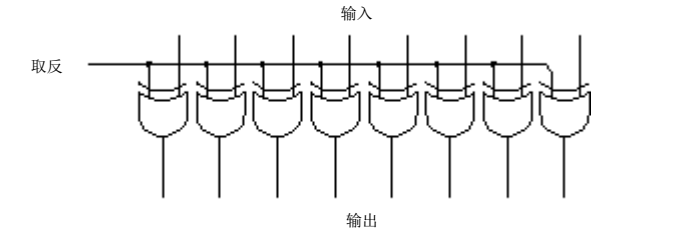
這個電路實現了把輸入的資料取反（0->1,1->0）

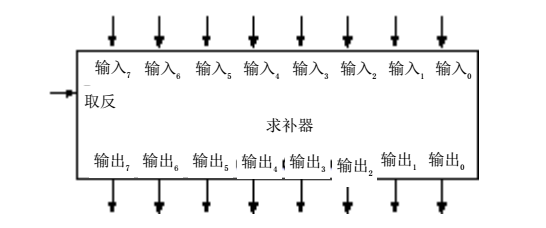
這是求補器的“抽象”

減法的邏輯實現我直接給出，相信讀者也應該能看明白

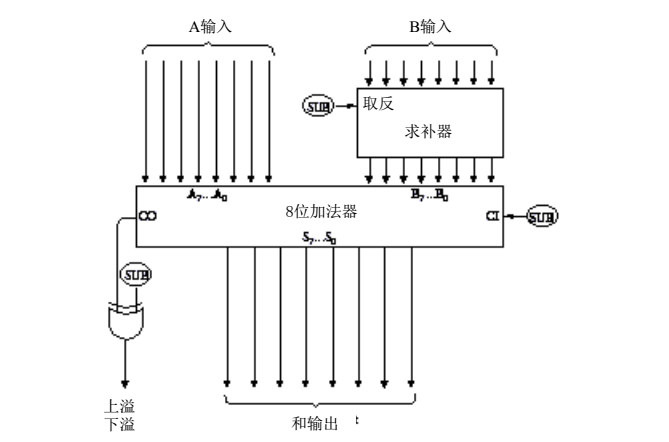
我還清楚的記得，在計算機組成這門課上，老師講述，原碼和補碼概念，“在計算機內部，正數的補碼是它本身，負數的補碼，記得取反加1“，為什麼取反加1呢？看看上邊的實現，計算機內部如何實現減法？有個取反操作，還有個進位操作，這不正是”取反加1“嗎？

下面從邏輯實現層，回到物理層，思考下，需要多少繼電器才能實現這樣的 ”小發明“，算了，嚇一跳吧？然而我們的計算機先驅康拉德·楚澤花費了十年心學，3000多個繼電器才早出一個計算機原型，所以，，，本著向先哲致敬的精神，讓我們在大腦中”打造出“一臺計算機

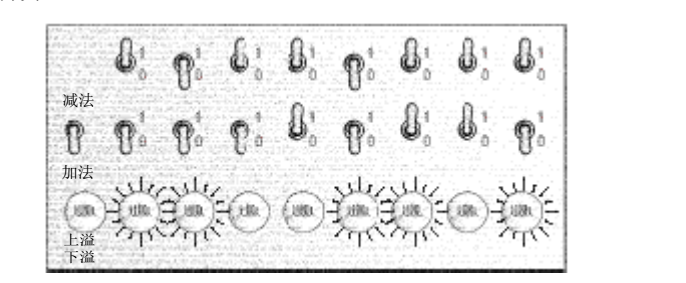
”我的專利不僅僅能實現加法操作，也能實現減法操作，計算具有普遍性，具有劃時代的意義，可以把人類從複雜的計算中解救而出來...“

至此，我們實現了一個簡單的計算器實現，不難吧？然而這才只是萬里長征的第一步。

接下來我來說說，計算機是如何儲存資訊的，這真是個費力活兒，在不太遙遠的過去，二十年前，計算機的儲存量還非常有限，我記得初中那會兒還沒有MP3，用磁帶聽歌，直到最近，儲存技術才有了長足的進步，當然這是後話。

第二節，計數器

人類的感官，聽覺，觸覺，味覺，視覺，感官器官接受外界的刺激，在大腦中留下神經訊號，進而形成對“外部世界”的認識，那抽象的事物怎麼去認識呢？

電燈通電點亮燈泡，高中的物理知識解釋，足夠了。電可以讓物體運動，這個道理人人都懂。坐在回家的高鐵上，讓我想想一下高速列車是如何運動的：駕駛員按下通電按鈕，帶動電車引擎，電車引擎通過傳動裝置把牽引力傳給電車車輪，列車得以啟動。高速列車的動力系統也相當複雜，我不瞭解每一個實現的細節，但是我可以想想出電車引擎的工作原理，為什麼？因為這些都是實實在在的實物，看得見摸得著。那我想想出計算機的工作原理嗎？答案是不能，為什麼？因為計算機一層層的“抽象”，一個小小的物理器件上集成了上億的基本元器件，使計算機真正的工作原理是我們越來越遙遠。

下面還讓我們回到19世紀末，二十世紀初，那個激盪人心的電力革命的年代，讓我們去還原真實的技術實現過程。回到高中物理課堂

我們已經講解了如何去製造一個一臺簡易的“計算器”，不知不覺下課了，這時我聽到一陣刺耳的下課鈴聲。電鈴和計算機有關係嗎？我直接上圖吧

注意看旁邊的那個金屬小錘子

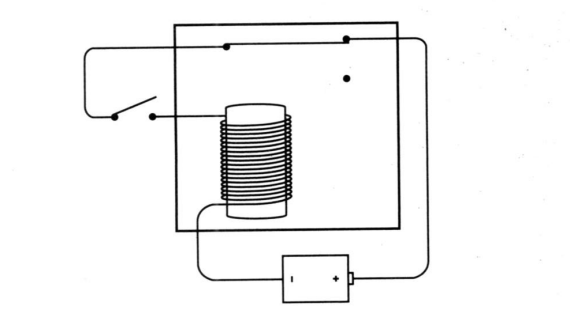
電鈴的工作原理如上圖所示，大家想象下，電鈴的小錘子震盪起來敲打金屬蓋發出聲音的情形，duang,duang,daung,形象吧？（這種電路叫做震盪器）

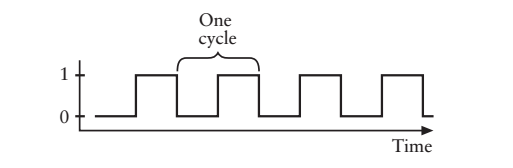
振盪器是不是可以實現計數功能呢？交替的輸出0和1，哈哈，感嘆造物的神奇吧！

下面我們再來看一些神奇的電路，當初的先驅們是怎麼想到這些複雜而精緻的設計

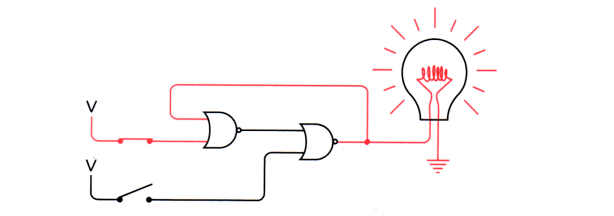
閉上上方的電路，燈亮了

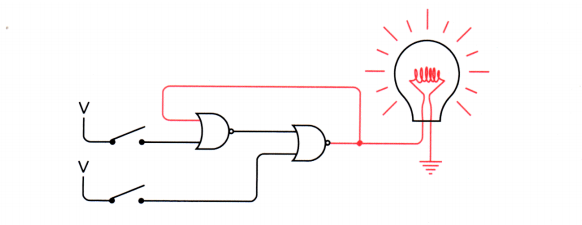
斷開上方的電路，燈依然在亮

閉合下方電路，燈滅了

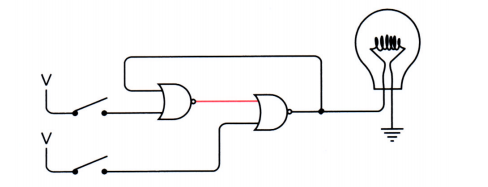
斷開下方的電路，燈依然不亮

電路的奇特之處在於：同樣是在開關都斷開的狀態下，燈泡有時候亮，有時候不亮，當開關都斷開時，電路有兩個穩定狀態，這類電路叫做“ 觸發器”。（英國物理學家1918在工作中發現的）

觸發器電路可以保持資訊，確切的說，可以“記憶”某些資訊，他可以“記憶”那個開關先閉合。觸發器是一個大家族，大家要是有興趣可以去看相關資料。請記住一點！觸發器是用來“記憶”資訊的，我再給出兩類常用的觸發器

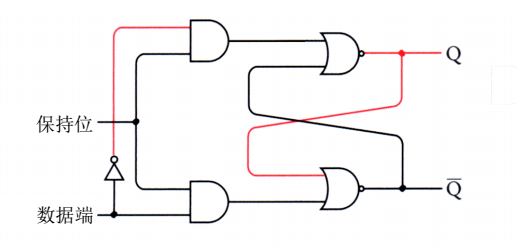
這個叫做“D型觸發器”，具體實現如上圖，我們的表示一直都停留在很“底層”，一直都很關注實現的細節，隨著細節實現越來越多，我們需要上升到高一層的層次，更加關注功能的實現，而不是陷於細節實現的泥潭！（想一想，為什麼說，計算機具有與生俱來的層次結構）

資料端簡寫為D，時鐘端簡寫為Clk，功能表如下：

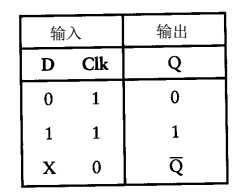
腦袋裡想象下，觸發器是一個很聽話的孩子，當clk端通電時，相當於告訴孩子，“孩子啊，你要記住我傳給的資訊”，clk斷電時，孩子在自由自在的玩耍，完全不接受任何傳過來的指令，很形象，不是嗎？

在D型觸發器的基礎上實現了更復雜的功能，“ 邊緣觸發的D型觸發器”

“抽象”圖

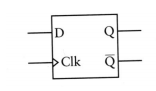
again，抽象的思想，使我們脫離的細節實現（上圖），更加關注功能

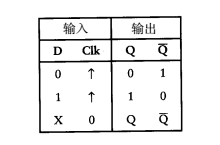
向上的箭頭，表示電訊號從0到1變化的那一瞬間有效，再次在腦袋裡想象下，觸發器是一個很聽話的孩子，當clk從0->1變化時，相當於告訴孩子，“孩子啊，趕緊接住我給你的球，球在這裡指資訊”，其他狀態下，孩子在自由自在的玩耍，完全不接受任何傳過來的指令。

有人問，說了這麼多，到底想幹什麼？好的，告訴你，用這些可以實現一個計數器，記得小孩子學數數嗎？我們要做的的就是要用機器來從0開始數數，真的嗎？恩，離這一步已經很近了，不信看下邊

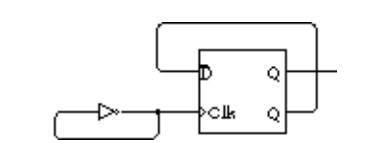
簡單的，把振盪器和觸發器相連

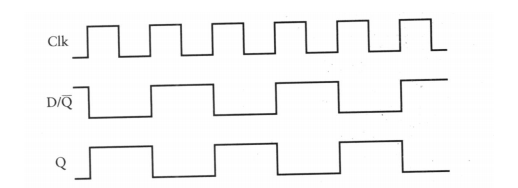
電平訊號的變化

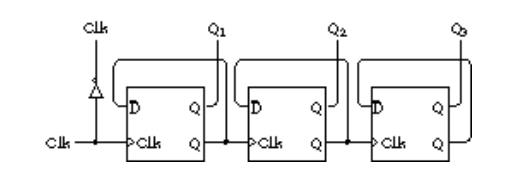
稍微擴充套件一下，實現更復雜的功能，應該能看明白吧

電平訊號的變化（標上0和1）

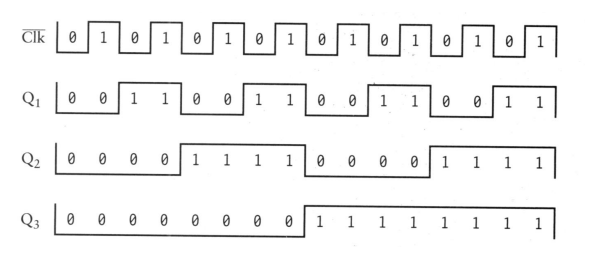
嗨嗨，清醒下，我們得到了什麼？把上圖順時針旋轉90度，你發現了嗎

這不就是在計數嗎？用二進位制的方式計數！

把8個觸發器連線在一起，然後放入一個盒子裡，構成了一個8位計數器，能從0數數到2^8-1，（0-255），這個計數器稱為“8位行波計數器”

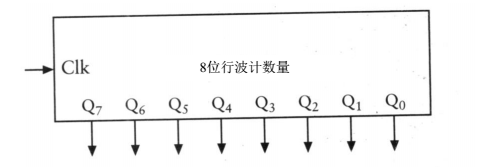
現在，我們已經懂得如何繼電器來做加法、減法、計數了，這一件很有成就感的事兒，使用的技術也是100多年前就存在的技術。

第三節 儲存器

我想用繼電器打造一個儲存量為64K x 8的儲存陣列，我能實現嗎？這會兒可是在二十世紀初！如果我穿越回那個年代，一定會再次為我的“發明”申請專利，如果真是這樣，那計算機的發展史上會留下我的名字（呵呵，意淫一下），下面就看看我是如何實現我的“發明”吧

上節，我已經提到，觸發器可以“記憶”1位的資訊

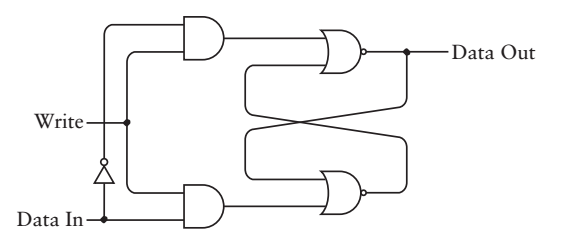
就是上圖這個樣子，我們把它抽象成：

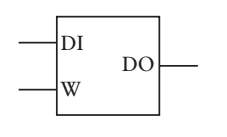
我們把上圖稱作“1位鎖存器”，想一想，兩個輸入線和一個輸出線都是什麼意思，我上節已經解釋過，來、來、來，想一想那個淘氣的小朋友。

有了“1”，那麼距離“100000”還會遠嗎？無非就是如何組織n個“1”，“抽象”的量級提升的過程

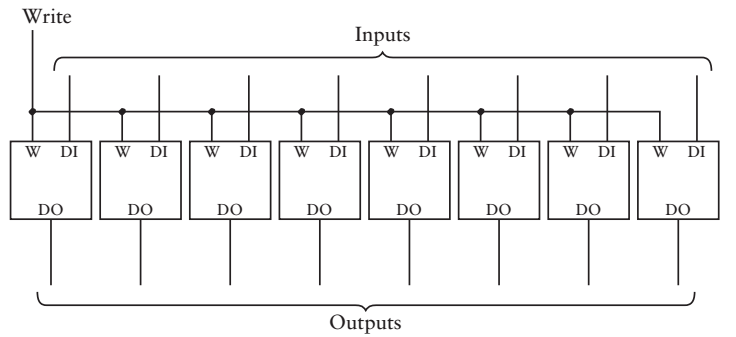
這是8位鎖存器

簡寫成這種形式

再來看兩個神奇的發明，或許你也會為發明者神奇的構思所折服

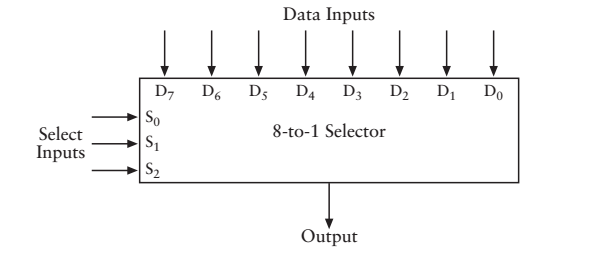
我想製作出這麼一個元器件，他要實現這些功能。想想一下，某一天，你成了一個名人，每天前來拜訪的人絡繹不絕，今天呢，來了八個人，但是你時間有限，只能見一個人，那就讓5號來吧（把拜訪者編號，0-7），5號拜訪者帶來了自己的禮物（0或者1的資訊）。看圖，左邊的三根線表示拜訪者的地址（當然是二進位制編碼），000,001,010,011,100,101,110,111,5號就是101，這時候呢，我只需要把S0和S2通電，那麼5號拜訪者就進來了，獻上自己的禮物（1位的資訊）。

怎麼實現這個功能呢？有興趣的自己去研究下面實現，請記住，我們現在討論的內容抽象的層次已經不是最最底層的實現了，而是更加關注於邏輯器件實現的功能

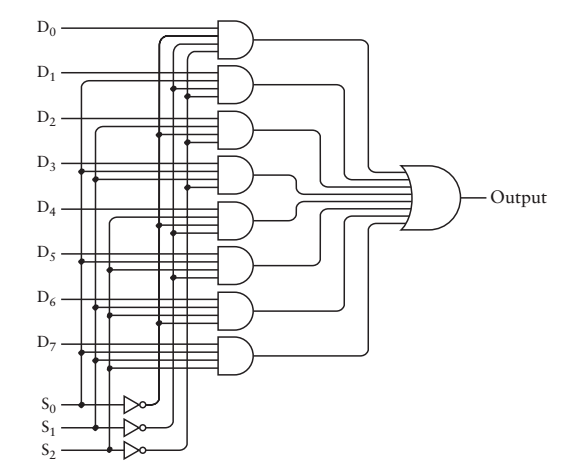
這叫“8-1選擇器”

反過來，我有一封信需要送出去，這封信的內容是0或者1，現在我也有8個快遞小哥可以選擇，編號分別是000,001,010,011,100,101,110,111，我讓誰去給我送信呢？那就還是5號吧，於是我把地址分別設定為101,5號小哥就去給我送信了，給出具體實現，有興趣的自己去看吧

這個電路名兒叫做“3-8譯碼器”

有了8-1選擇器和3-8譯碼器，就可以製作出一個8位儲存器了

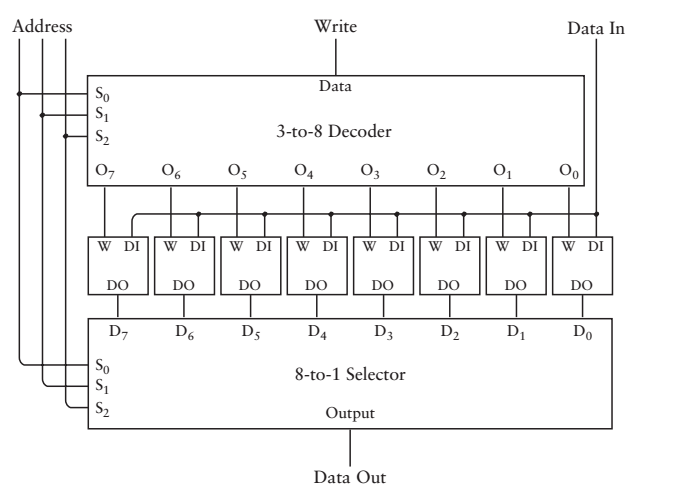
again，把複雜的電路實現，抽象成簡單的符號表示

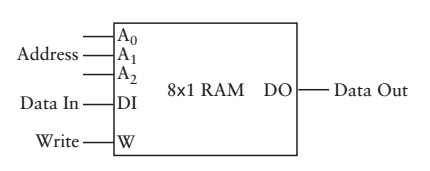
讀/寫儲存器，通常叫做隨機訪問儲存器或者叫RAM，RAM可儲存8個單獨的1位資料

如何得到16 X 1的RAM呢？相信大家都能想到，用2個 8 X 1的RAM，我彷彿回到了《計算機組成》的課堂，讓我再來做一次作業吧

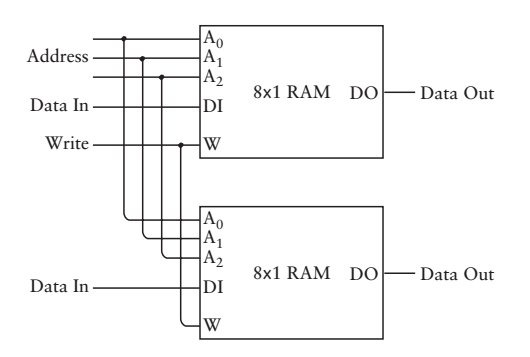
簡寫如下：

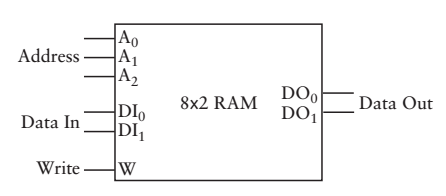
這種方式或許正確，但是使用了三根地址線，兩根資料線，能不能使用4根地址線1根資料線呢？

加一個2-1選擇器不就行了嗎？（設計一個2-1選擇器，這會兒應該不算什麼難事兒）

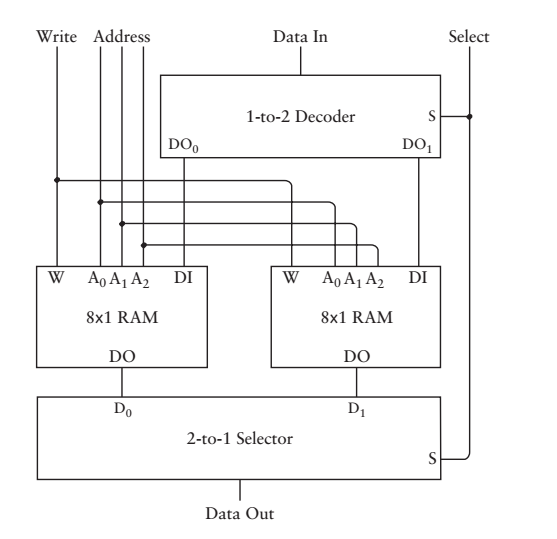
再次用符號簡寫：

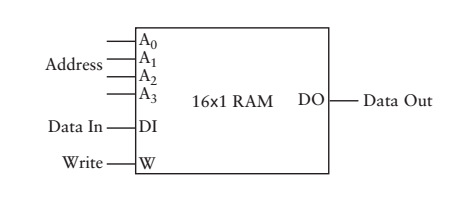
回到我們的出發點，怎麼得到64K X 8的儲存陣列呢？

無非就是努力提高8位鎖存器的整合程度嘛，我可以想象，讀者看到這裡，腦子裡全是密密麻麻的的連線，或許你還一時想象不到連線的方式，但是看到這裡，64K X 8的儲存陣列一定能用某種方式實現，對吧？雖然沒有實現其電路圖，但我也可以說，我理解了儲存器工作原理，（你懂了嗎？）。

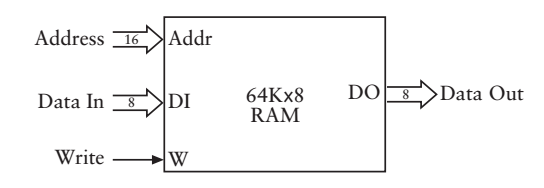
1024 X 8RAM的符號表示，2的16次方，即64K，地址線有16根，資料線有8根

為了申請我的專利，我需要做出一個機器的外部殼子，和第一節中的“計算器”一樣，把這個機器的殼子把我所有實現的過程封裝起來，形成一個“黑盒”，只保留幾個外部的介面（也就是那幾根資料線，一定要記得他們的功能），我要做成的外部盒子是這個樣子

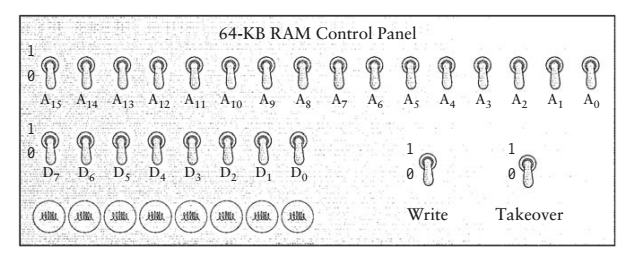
上一排的對應16根資料線，下一排有8根資料線，這個不用解釋，相信把上文看完的都能明白什麼意思，takeover這個按鈕表示是否使得當前控制面板處於“啟用狀態”，也就是說，這個開關的作用是確定由控制面板還是又外部所連線的其他電路（從來沒說過，沒有連線外部其他電路，或者想象下，我這個機器殼子外面有一排的針孔，外部電路可以接進去，想想電腦機箱後邊的針孔，就是這個意思，Soga）來控制。如果有其他電路相連。這時候takeover為 0（圖示狀態），此時儲存器由其他電路接管，控制面板上的其他開關不起作用，當takeover為1 時，控制面板將重新獲得對儲存器的控制能力。

最後還是給出電路實現

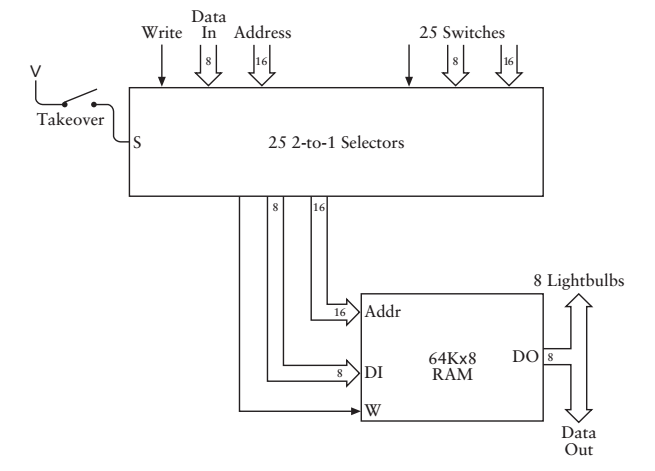
想一下，機器殼子後面的針孔連那裡，控制面板的開關又連線哪裡？

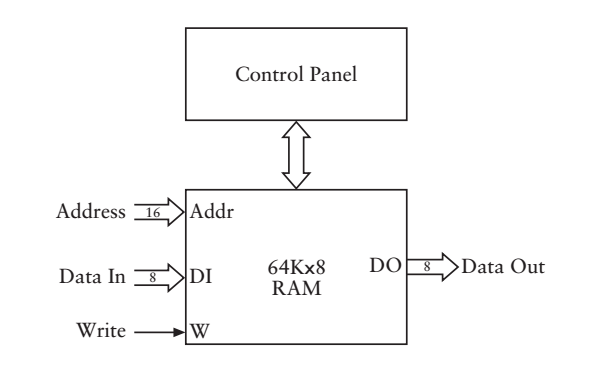
簡化的圖示，是不是又用到“抽象”的思想呢？

一個辛辛苦苦裝滿65，536位元組（8位為一個位元組，位元組編碼請去參考ASCII編碼）珍貴資料的64K X 8的RAM陣列，如果斷電，會發生什麼事情？首先電磁鐵會因為失去電流失去磁性，隨著“梆”的一聲，金屬片講彈回原位，RAM中的所有資料將如風中殘燭一般消失在黑暗之中，所以，RAM也成為“易失性”儲存器。

那我一手打造的64K X 8的儲存陣列，需要多少繼電器呢？答案是是500W左右，是不是驚訝到恐怖呢？誰會沒事兒造出這麼個恐怖的怪獸？（100年後的今天，用二極體，三極體，整合這麼多元器件的晶片，連指甲蓋的大小都不到，感嘆人類技術的進步吧）。

我穿越回二十世紀初，再次站在專利局的門口，為我這項“偉大的發明”申請專利，瑞士專利局的愛因斯坦會因此嚇尿嗎？世界上最聰明的大腦，能理解“黑箱”背後發生了什麼嗎？

第四節 自動操作

說了這麼多電子線路的知識，我相信的我的講述方式，大家都是能看懂的，前面所寫的，其實只是為大家講述一件事兒，“把電子元器件內部實現展開”，現有的一個個電子元器件，現在就是一個個小工具（把內部實現封裝起來，保留外部介面，外部介面，就是那一根根地址線，資料線，和其他開關）、原材料。那我們現在看一看現在都有那些原材料呢？

計算器：一個會算數的小朋友，每次你把要進行計算的兩個數給他，拍一下小朋友的頭，小朋友幫我算一下吧，他會把計算的結果給你，沒有一點誤差，計算速度很快，並且樂此不疲。

計數器：一個一直在數數的小朋友

儲存器：辛辛苦苦裝滿了64K 位元組的箱子

譯碼器:《唐伯虎點秋香》中有個代號，9527，一個數字，你說它什麼意思呢？如果，我“規定”9527指的是唐伯虎，讓譯碼器來做這件事，譯碼器你把9527給我帶過來（地址線用2進製表示9527,9527的二進位制是多少呢？），這時候譯碼器“很聽話”的把唐伯虎叫過來。（在這裡，機器“理解了”人類的語言嗎？）

有了這些原材料，我們就可以著手打造一臺computer了，我們的工作才剛剛開始，請讀者保持耐心，我們最終要實現的是一臺通用計算機，這臺“先進的”機器可以使加減法的過程自動化，is that unbelievable？這臺機器可以解決所有能有加、減法處理的問題，而事實上現實中的許多問題確實可以用加法與減法來解決。

讓我來回顧一下自己的教育經歷。從咿呀學語之後，幼兒園開始，我們就要開始一生的學習了，小學的數學課現在還叫不叫“算數”？剛開始，我們扳著自己的手指數數“1,2,3,4,5，上山打老虎...”,學會數數之後呢？老師先教我們加法與減法，那麼乘法和除法呢？我依稀記得，是用加法和減法來實現的，對嗎？

加法與減法，可以從底而上，構建更加複雜的算數系統，以至於，微積分也是建立的基本的算數系統之上，我還清楚的記得泰勒公式帶給我的震撼，記得第一次見到牛頓迭代法時的情景。

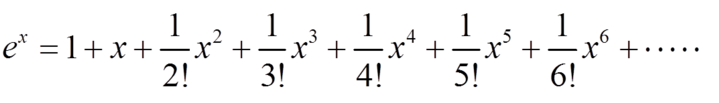
最美的數學公式之一，不解釋為什麼了，參考大學微積分

假如，假如我們已經實現一臺可程式設計的最原始的執行加減法運算的“計算機”，如何計算出e的值呢？

想明白這一切，就需要我們瞭解“自動操作”的過程，瞭解程式的本質什麼？編寫程式的過程就像堆多米諾骨牌，辛辛苦苦，小心翼翼堆了半天，只為了那一下推到骨牌的快感！下面這一部分內容較難，請讀者一定保持耐心，我會試著按我自己的理解講清楚，如果我有理解不對之處，歡迎大家指出來，討論改正

新紀元-能接受“指令”的計算器

有人問我，真的可以用上述提供的那些原材料（計算器、計數器、儲存器、譯碼器）造出一個計算機嗎？就像維克多·弗蘭肯斯坦組裝怪物一樣，當一切都已經就緒，看著我們一手打造出的龐大的怪物，小心翼翼的通上電，“醒來吧，孩子”，就像給他賦予生命一般，這些破銅爛鐵奇蹟般的甦醒過來，按照我給他的指令，完成我想要的工作，真的，人世間沒有比這樣的工作更讓人神往了，你能理解《模擬遊戲》中Turing對克里斯托弗的一往情深嗎？至少他打動了我的心。

扯多了，我可以很明確的告訴你，只用那些原材料確實可以打造出一臺計算機，並且歷史上確實有人實現了！是誰？馮諾依曼？圖靈？很遺憾地告訴你，no。主人公的名字，我前邊已經提到了，他叫康拉德·楚澤，1935年還是一個工科學生的他，在位於柏林的家中打造出一個可程式設計的計算機，一共花了3000多個繼電器。

接下來讓我們穿越回到1935左右，讓我們跟隨“主人公”的思路，嘗試打造出一臺“計算機”。

還記得上小學時，你學完數數，學完加減法之後，大人們常常考考你的題目是什麼？“你給我算一下從1一直加到100吧”，問題是，我能用機器代替我來算數嗎？哦哦，簡單，我的原材料裡不是有“加法器”了嗎？，稍作修改就行，好，看看我的設計

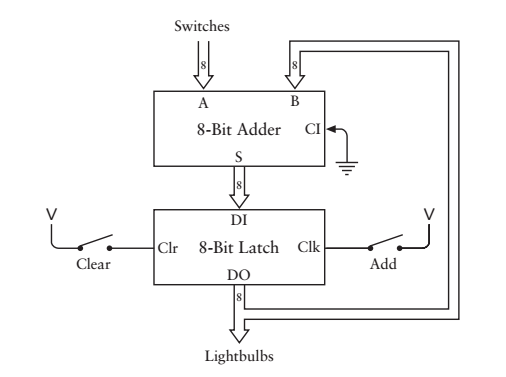
拿一個8位的加法器和一個8位的鎖存器，按上述方式相連，每次我們可以通過加法器的開關輸入我們要算的數（當然要輸入的數是0-255之間，計算的結果也是0-255之間，在這裡可以先計算1-10的和），我們小心翼翼的撥動開關，最後下方的一排指示燈顯示計算的結果。簡單吧（這個器件稱作累加器）可是我一不小心輸錯了一個數怎麼辦？只有重新來算，完全再來一遍，好麻煩啊，有沒有可以改進的方式呢？我突然想到，不是有儲存器嘛，可不可以把我要計算的資料先存入儲存器，再通過讀取儲存器的內容，把資料傳送到加法器，執行運算，最後顯示結果。

good idea！具體該怎麼做呢，我給出一種實現方案

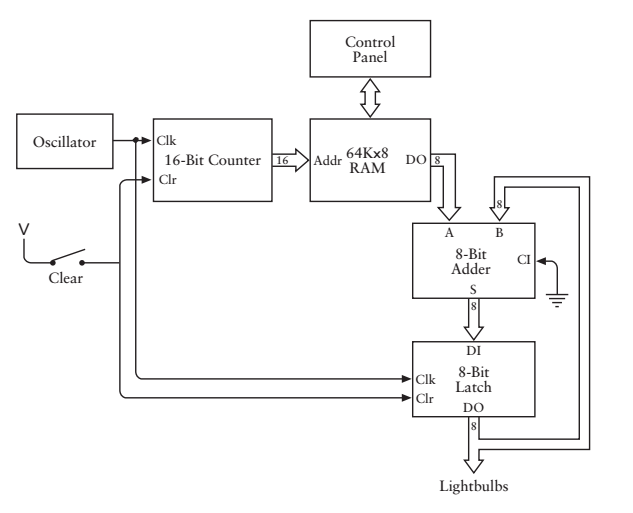
一個振盪器（想想duang，duang，duang的電鈴），16位計數器（我們的儲存器容量不是64K X 8麼，需要16根地址線），一個64K X 8的RAM（RAM連線控制面板，控制面板可以輸入資料，還記得控制面板的takeover按鈕是做什麼用的麼？），一個8位加法器和一個8位鎖存器。

讓我們閉上眼睛，來想一想，這是怎麼工作的。首先，請清零開關，然後閉合控制面板上的takeover按鈕，這時候控制面板接管了儲存器，如果要算的有100個數，我們一次調整儲存器的地址線和資料線，把資料存入0000h-0063h的地址空間（這一部分你明白了嗎，該怎麼操作控制面板呢？上述地址空間用16進製表示）。資料輸入完了，我們斷開控制按鈕（takeover鍵），這時候控制面板失去對儲存器的控制，斷開清零開關，這時候，計數器開始工作，0000h，電訊號傳入儲存器的地址線，儲存器呢，是一個忠實的倉庫保管員，來，我看看你要取什麼東西，他接過傳來的地址，哦原來要0000h盒子內的東西啊，好，你拿走吧，（0000h“盒子”內的東西就是剛才輸入的第一個數），第一個資料傳入到加法器，加法器小朋友一看，好了，你和自身相加，這不還是你自己嗎？他把計算結果給了鎖存器，鎖氣器把計算的結果放入一個臨時的盒子內。經過一點時間（很短）計數器變成0001h，還是和剛才一樣，計數器小朋友把自己的數給儲存器管理大叔，大叔根據傳過來的數，把取出的資料傳給加法器小朋友，加法器小朋友執行加法運算，把得到的結果給鎖存器。他們是如此的兢兢業業，樂此不疲，“機械式”的完成自己的任務，沒有一點兒怨言。

哎，計算的結果是什麼？我怎麼看到指示燈在閃爍，計算的結果哪裡去了？哦哦哦，計數器小朋友實在是太敬業了，根本沒有辦法讓他停止工作，當他數到FFFFh之後又從0000h開始數數了。

還有這樣的計算也太機械了，功能也實在是太有限了，要是我想把100個數，分成50組，計算每一組的和，這又該怎麼做到呢？聰明的讀者你也動動腦袋想一想，怎麼做到呢？

楚澤看到這裡也許和咱們一樣皺緊眉頭，怎麼做呢，怎麼做呢？該怎樣解決這個問題呢？這時候或許突然迸發出“革命性”的想法，把運算的結果存回到RAM陣列中不行嗎？這樣一來，就可以在適當的時候用RAM陣列 的控制面板來檢查運算結果（按下takeover），為了實現這個目的，在控制面板上加一排顯示燈。eureka！

改變之後的連線圖

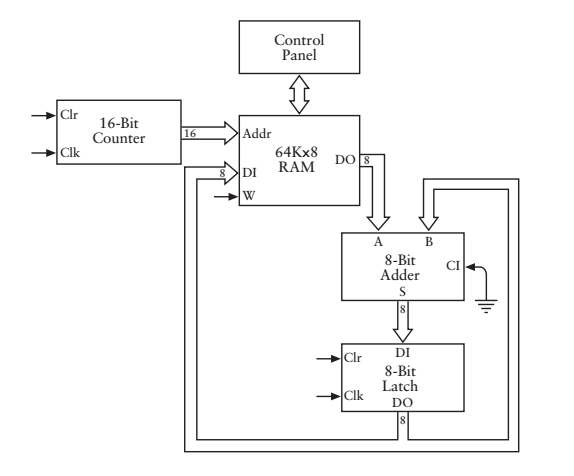
這裡略去了一部分，包括振盪器和清零開關。這樣做是很好，但是問題來了，怎樣控制RAM寫入訊號呢（何時存入RAM，把結果存在什麼位置？）

假如我有一個這樣的計算任務要完成：首先對三個數進行求和，然後對兩個數進行求和，最後再對三個數進行求和，圖示如下

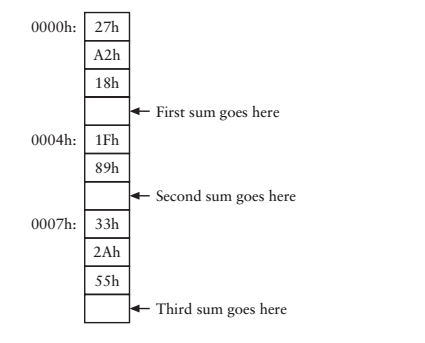
圖中用一小段連續的紙條（標記上連續的格子）表示一小段儲存器，格子內表示存的內容。怎樣使自動加法器為我們完成這項任務呢？我們不能期待向RAM陣列中輸入一組數，然後自動加法器自動完成任務，自動加法器怎樣“理解”我們交給它的任務，它怎麼“知道”我們要他們幹什麼？

為了完成這個任務，我們需要用一些數字程式碼來標示加法器需要完成的每一項工作：載入（Load）、相加（Add）、儲存（Save）、終止（Halt）

有了上述的指令，我們就可以命令計算器來工作了（暫時不去了解如何實現），對於上述的任務，可以表示如下：（1）把0000h地址處的內容載入到累加器（2）把0001h地址處的內容加到累加器（3）把0002h地址處的內容加到累加器（4）把累加器中的內容儲存到0003h地址處（5）把0004h地址處的內容載入到累加器（6）把0005h地址處的內容加到累加器（7）把累加器中的內容儲存到0006h地址處（8）把0007h地址處的內容載入到累加器（9）把0008h地址處的內容加到累加器（10）把0009h地址處的內容加到累加器（11）把累加器中的內容儲存到000Ah地址處（12）命令自動加法器停止工作

有了這些指令程式碼，那麼這些指令程式碼存放在哪裡呢？得了，不去想了，簡單粗暴的解決方式就是在加一個RAM，一個RAM存放資料，另一個RAM存放資料對應位置的操作符（也就是上文指定的那些程式碼），再次對我們的機器進行改造，改造後的結果如下

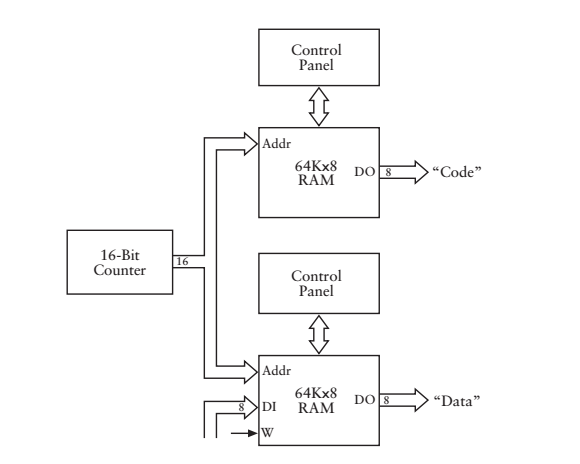
觀察要仔細啊，資料的RAM即可以通過Control Panel控制面板進行輸入，也可以接受外部的資料，而儲存程式碼RAM只能通過控制面板寫入！

那麼往儲存程式碼的RAM裡寫入什麼內容吧？機器又不認識load、store、add、halt這些單詞。既然機器不認識，我就讓他們認識！解決方式，就是編碼，其實兩位資訊編碼足夠操作碼，程式碼Load（載入），10hStore（儲存），11hAdd（加法），20hHalt（停止），FFh

這樣一來，儲存程式碼的那個RAM裡邊要存的內容就一目瞭然了

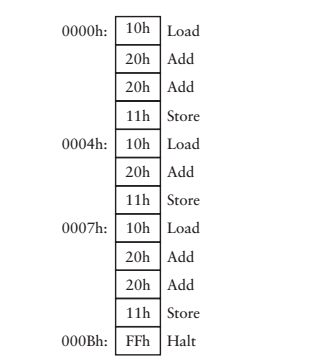
看到這裡，讀者有疑問嗎？還是我最早提出的那個問題，機器是如何“理解”人類的語言的，我雖然把要操作的指令用0和1進行編碼，但你把編碼之後的內容拿給我們一手打造的這臺機器，他還是“不明白”什麼意思，去進行何種操作啊！我們轉來轉去又轉回最初的起點，你讓冷冰冰的機器去“理解”人類的指令，無異於天方夜譚，機器就是機器，永遠也不可能具有思維，當初，我在這裡也是困擾好久，哦，原來如此！

我已經把答案告訴你了，機器就是機器，永遠也不可能具有思維

我不管你有沒有思維，你必須完成我給你的任務，你把上述的任務算個結果出來，這一點兒或許能辦到，嘻嘻

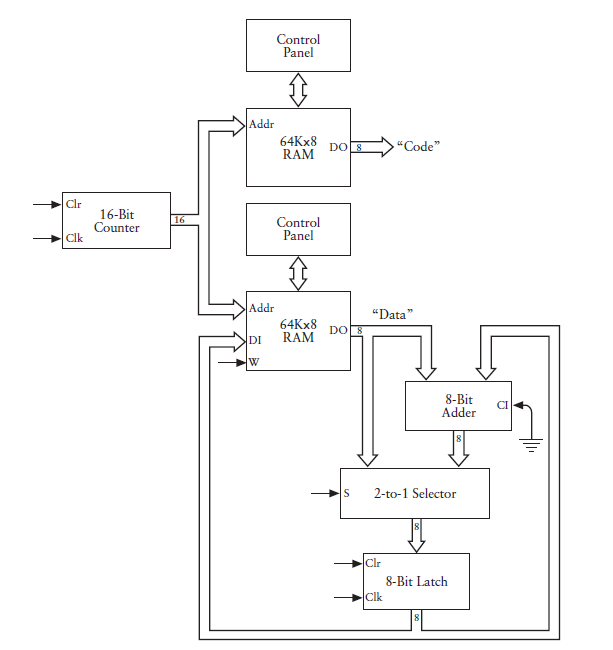
為了體現Load和Add命令，我的機器內部又進行了部分改變，你看出差別來了嗎？

其實上述有一小部分沒有連線。again，閉上眼睛，跟我來想想機器執行的過程，可愛的小朋友們和敬業的大叔們又來了。計數小朋友把資料給兩個RAM的倉庫管理員，一個取出資料，一個取出指令。資料傳給累加器和2-1選擇器（這是個什麼鬼）？資料到了2-1選擇器小朋友的面前，發現了一道門，門上寫著，“此山是我栽，此樹是我開，要想從此過，留下買路財”，小朋友，讓我過去吧，叔叔給你糖吃，2-1選擇器小朋友說，“我只有一條路，你們兩個人，我讓誰通過呢？”（圖中，2-1選擇器接收了兩組資料），就在這時候，2-1選擇器小朋友，收到了一條指令，這條指令來自哪裡呢？哦哦，剛才管程式碼的RAM大叔，取出指令（10h或者，11h或者20h或者FFh），他把指令交給“指令解析器”（圖中沒有畫）指令解析器負責把信送給2-1選擇器、RAM、計數器的指令接收端（也就是2-1選擇器的S，RAM的W等，在這裡稱為控制訊號，控制訊號決定機器中某些部件是否工作或者決定某些期間如何工作。例如，如果程式碼RAM陣列輸出是load指令，2-1選擇器S端收到0，如果程式碼RAM陣列輸出是Add，2-1選擇器S端收到1，操作碼是指令Store時，資料RAM陣列的W收到1。實現“指令解析器”很困難嗎？想一想第二節中是如何送信的，3-8譯碼器，譯碼器實現只是一種方式，當然也可以用邏輯閘來實現、你明白了嗎？），2-1選擇器小朋友收到了0，也就是要執行Load操作，8位鎖存器把臨時資訊儲存起來。然後計數器小朋友又開始數到了0001h，這些勤勞的小朋友和勤勞的大叔又繼續工作了...

用這種方式，我終於實現了我的想法，這真是一件值得高興的事兒，我要好好休息下，等等，休息之前，順便擴充套件一下我們的機器，讓它也能運算減法。好簡單，增加一條指令不就行了？Subtract（減）

相應的，機器內部實現再改造下，增加一個取反器

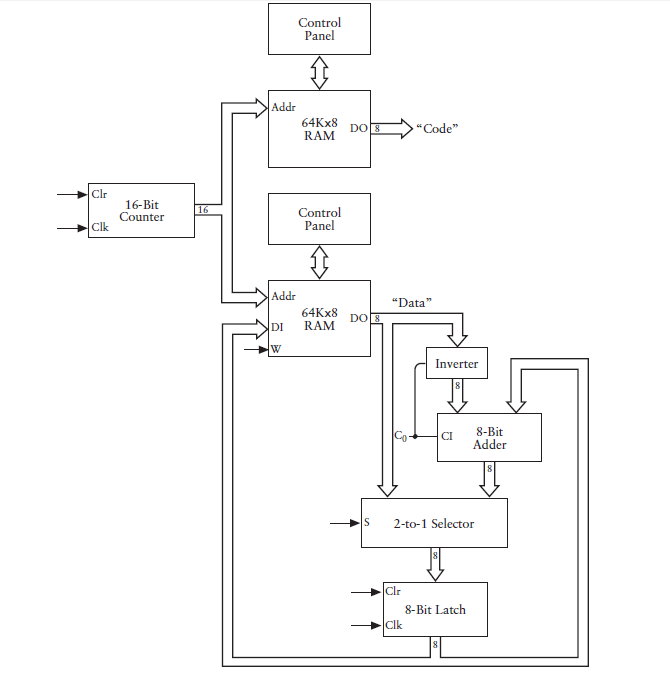
佈置一道作業題，取反器的那根控制訊號線接在哪裡？

資料“流水”

我們從繼電器打造出閘電路，進而實現加法器，計數器，儲存器，都是為了向我們的那個終極目標一步步前進。這就像點亮科技樹的過程，一步步提高，直到實現我們的終極目標--一臺可程式設計的通用計算機，那現在來看看，我們的科技樹點亮到哪一步了，現在我們親手打造的“能讀懂人類指令的計算器”，離我們的目標還有多遠？

來看看我們這臺機器能不能完成我們想要完成的任務。假設現在要把56h和2A相加，然後再從中減去38h，結果是多少呢？不是有指令了嗎？來，設定指令，讓機器去完成

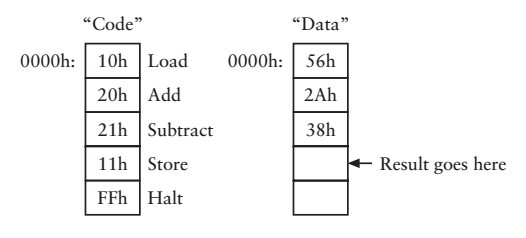
由於指令和資料是分開儲存的，我們分別通過控制面板在RAM中輸入資料，啟動機器，機器就“神奇”的計算出結果，可以用個控制面板來檢視計算的結果。

如果我的計算任務擴大一些，算一算1W個數的和吧？啊？10000個數，這時候我可以想象，站在臺機器前面的“主人公”滿臉苦逼的表情，我們小心翼翼的輸入這指令，Load ...，Add ...，Add ...，Add ...，......Store ...。然後我們再輸入資料，這真是個體力活兒啊！當我們終於把這一切都完成之後，啟動機器，Come on，baby！計算吧

讓我們再次閉上眼睛，想象機器工作的情形，計數器多麼像一顆跳動的“心臟”，過一段時間發出一次“心跳”，儲存器收到心跳的脈衝，從此中取出資料，資料被傳送到累加器“加工廠”等待處理，要通過一道道的“門”（2-1選擇器），最後會傳到儲存器。每每想到這裡，我不禁想起在歡樂谷水上漂流的過程，穿過一道道門，經過一間間屋子，每經過一道關卡，都可能被水淋到（資料被加工），最後轉了一圈回到起點，機器內部執行的過程，就是資料坐在船上“流水”的過程，不是嗎？

讓我們來看看機器算出來的結果，這可真是一個激動的時刻，辛辛苦苦撥了半天開關，現在要見證奇蹟了。“咦”？怎麼結果不對，這數值也太小了！

哦，原來如此，我的累加器只能算8位的資料，讓我去安靜的哭一會兒去。

你可能想到，把兩個8位的加法器連在一起構成一個16位的裝置，這是一種解決方案，但是，還有代價更小的解決辦法。

比如要計算76ABh+232Ch,最終結果是99D7h

我們可以把高低位分開來算

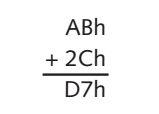
低位加法

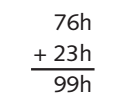
高位加法

最後把計算的結果寫回儲存器

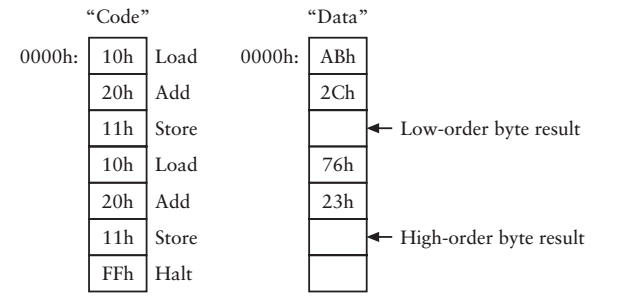
D7h被寫入地址0002h處，99h被寫入地址0005h處

這是很理想的狀況，因為，在上述的例子中把高低位分開計算，低位計算恰巧不存在進位的情況。如果要把76ABh和236Ch這兩個16位的數相加該怎麼做？ABh+6Ch=117h；1h+76h+23h=9Ah。計算的結果為9A17h，怎麼解決這個問題呢？可能有讀者已經想到了，加一個進位鎖存器（儲存進位）不就行了？那我再問一句，“那我們的指令碼是不是需要擴充套件一下呢？怎麼使得譯碼器來觸發讀取進位的訊號呢？”讀到這裡，讀者也應該和我一樣，我們現在不關心具體實現細節，一定會有某種邏輯閘的組合來實現，對吧？下邊我給出擴充套件的指令碼（也叫作操作碼）

上述指令中，增加了一個“進位加”（Add with Carry）和“借位減”（Subtract with Borrow）有了他們，就可以極大的擴充套件加法器的功能，而不僅僅侷限於8位資料的運算了，可以對16位，24位，32位，40位數進行加、減法操作了！比如對兩個32位數7A892BCDh和65A872FFh進行加法運算。僅僅需要1條Add指令和3條Add with Carry指令

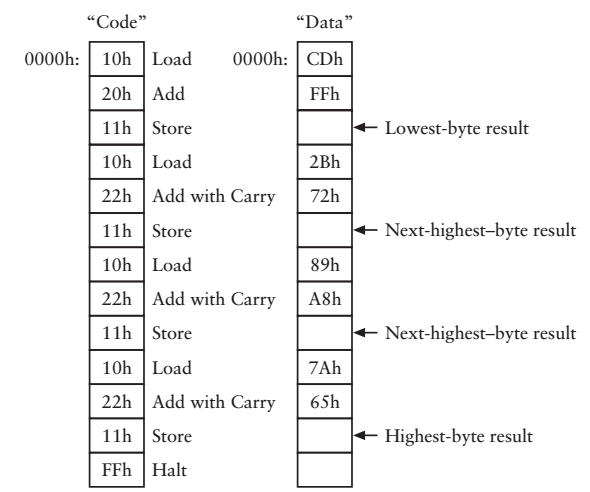
我們通過增加操作碼指令擴充套件的我們的“計算器”，在通往終極目標的路上又邁出了堅實的一步，“資料流水”的方式也確實也可按照我們的意願實現一些計算任務，但是，對於計算1W個數相加之類的任務，總不能期待一條條的輸入指令吧？

讓我們看看問題出在哪裡。第一，對於上圖來說，儲存計算結果的儲存單元地址不連續。第二。當前設計的自動加法器不允許在隨後的計算中重複使用的前面的中間結果，一旦我們把計算的結果寫回儲存器，我們就無法再次讀取它的值了。

產生上述情況的原因就在於，我們構造的自動加法器，程式碼的儲存和資料的儲存是同步的、順序的，並且只能從0000h開始順序定址，直至停機。

要解決這個問題，需要對我們設計的加法器做一個根本性且程度極大的改變。我想幾十年前第一代的計算機的設計者康拉德·楚澤，Turing等人一定會為這個問題寢食難安，因為解決了這個問題，才可以實現真正意義上的“自動操作”，這個問題也是計算器與計算機最根本的區別。

沒想到會有這麼多人點贊，謝謝你們的鼓勵，我們的萬里長征已經看到勝利的曙光了，馬上就要迎來激動人心的時刻了，請保持最後的耐心。

資料“轉圈圈”再次看一下我們設計的機器，程式碼的儲存和資料的儲存是同步的、順序的，並且只能從0000h開始順序定址（計數器小朋友在一次計數，告訴儲存器管理員大叔從哪個抽屜裡取資料），直至停機。但是，如果我的資料是連續儲存的，並且在任意地址儲存資料（也就是說，儲存器存放資料的抽屜式隨意的，我們只知道抽屜的編號），該怎樣去取資料進行計算，並且儲存計算結果啊？這時候我突然聽到一聲，“你傻啊，你把要取數和存數的抽屜編號告訴我不就行了？”，管理員大叔一語驚醒夢中人，是啊,有了儲存器的地址不就行了？可以把資料的地址與資料的內容分開存！這可真是石破天驚

那就再次改變我們的設計吧，

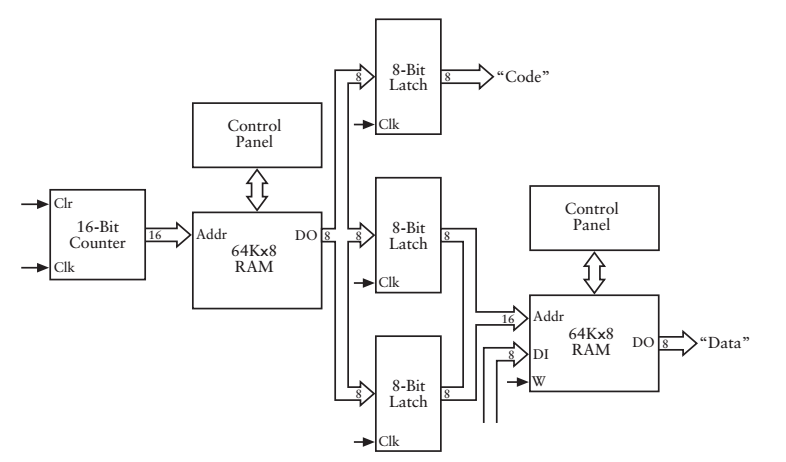
這次，我們把指令（程式碼和資料的地址稱為一條指令，先得到資料的地址，在根據地址取資料）放在一個RAM中，把資料存在另一個RAM中，並加了3個8位鎖存器（臨時存放8位資料），示意圖只畫出了改變的部分，其餘部分與原來保持一致（累加器和程式碼解析器還有相應的控制訊號）。指令佔1個位元組，16位的資料地址佔2個位元組，一條指令共佔用3個位元組，每次從RAM中取出1個位元組，所以每次取出一條完整指令需要3次計數，資料地址再次傳給儲存器（這裡多加了一個RAM），RAM取出資料傳給加法器，而程式碼的解析與資料傳輸到加法器進行計算操作也需要1次計數，這必然需要更加複雜的控制訊號。

從儲存器中取出一條完整指令的過程叫做取指令，機器響應指令碼的一系列操作的過程叫做執行指令，雖然機器可以自動取出指令，並執行指令，你能說它是一種“有生命”的東西嗎？

看到這裡有人可能要問，我們現在不是假設在1935左右嗎？RAM是很奢侈的（500W個繼電器），能不能想法捨棄掉一個RAM？把指令（程式碼和資料地址）與資料存在一起就可以了，這簡單，還記得2-1選擇器小朋友嗎？（儲存器部分提到了）

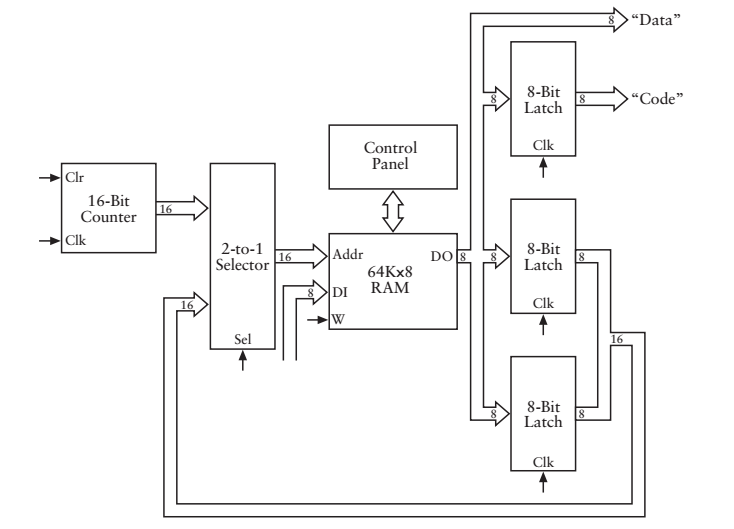
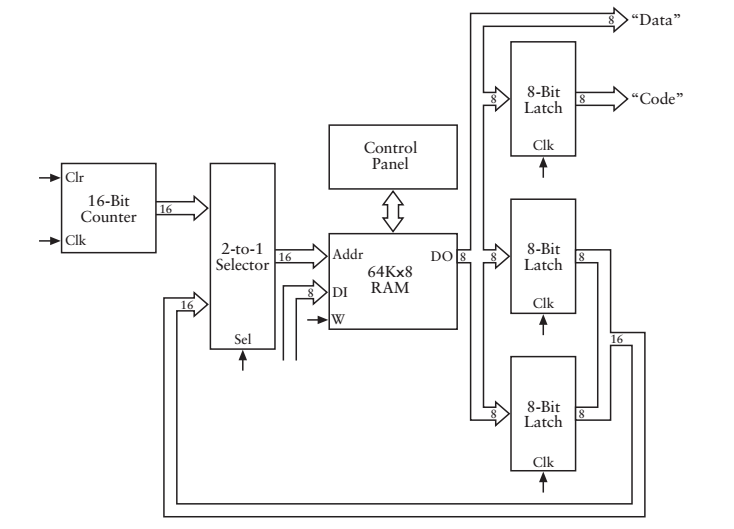
很簡單，得到資料地址之後，把地址回傳給儲存器（此時計數器小朋友的計數無效），再次根據地址取出資料。 來看一個小例子吧，計算45h+A9h-8Eh=?，假設45h，A9h，8Eh分別存在地址0010h，0011h，0012h處，計算的結果存於0013h處。我們應該給機器這樣的指令：把0010h地址處的位元組裝入累加器，把0011h地址處的位元組裝入累加器，從累加器中減去0012h地址處的地址，把累加器中的內容儲存到0013h地址處，停機，

資料的儲存可以是任意的，我們只需要知道其相應的地址，那麼指令呢？指令還是機械的順序的往下執行，會不會出現這種情況，順序執行指令，可是資料和指令地址衝突（要存指令的地址處已經有了重要的資料，需要跳過），指令能否跳過某一段區域，繼續執行呢？

這涉及到指令定址方式的改變（耐心聽下去，我們萬里長征，最終的一步來了，跨過他，前方就是一馬平川），怎樣跳過某一段兒區域，繼續執行指令呢？那就jump啊，對，擴充一條跳轉指令（Jump）

相應的機器內部實現也要改變

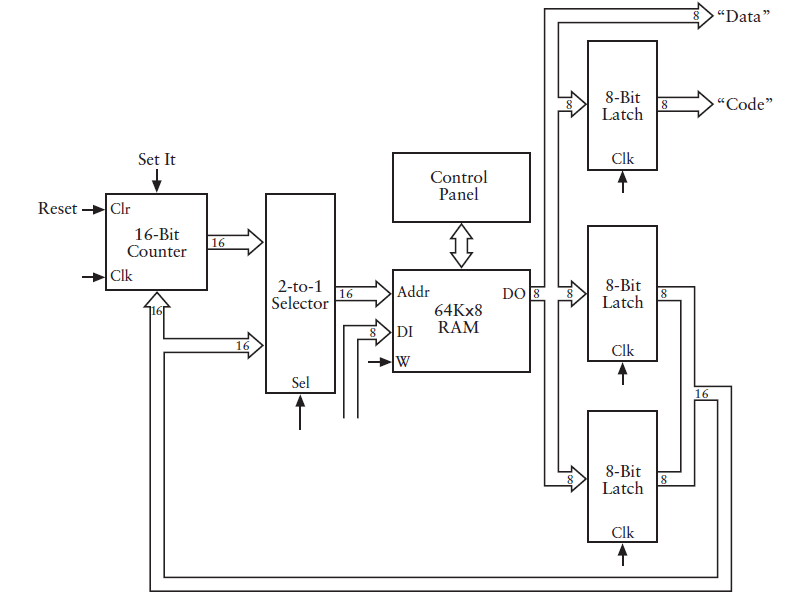
在上一步基礎之上，增加了一條到計數器的資料通路，相當於告訴計數器小朋友，“小朋友，你下次從我告訴你的那個數開始計數，叔叔給你糖吃，乖~”

讓我們回到電子線路中，計數器的實現，振盪器和D觸發器串聯方式（16個D觸發器），我們稍作修改一下邊緣型觸發的D型觸發器

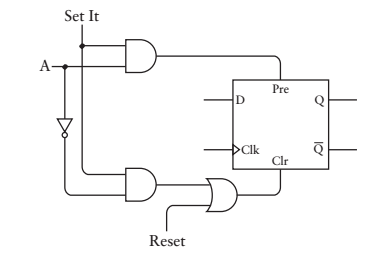
可以不用瞭解上圖的實現，請注意我們現在重點不在於具體實現，而在於實現某一功能，我們需要為16位計數器的每一位都設定一個這樣的觸發器。一旦載入了某個特定的值，計數器就開始從該值開始計數（是不是用糖果把計數器小朋友收買了，呵呵）

Jump（跳轉）指令確實很有用，但是一個有條件的跳轉更有用（“我是個有原則的人，除非滿足我的條件才jump”），比如要計算A7h與1Ch（十進位制的28）相乘的結果，和28個A7h相加的結果相同，計算過程涉及到大量的重複操作

假設乘數和被乘數以及計算結果儲存在一下地址：

1000h:00h,A7h,(16位乘數儲存在此處)

1002h:00h,1Ch,(16位被乘數儲存在此處)

1004h:00h,00h,(16位乘積儲存在這兩個連續的地址空間)

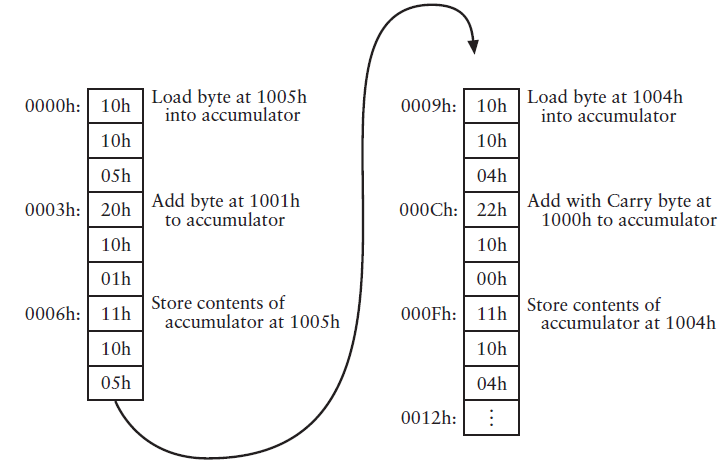
當這六條指令執行完畢之後，儲存器1004h和1005h地址儲存的16位數與A7h乘以1的結果相同。還要把這6條指令反覆執行27次才能達到乘法的目的，如果在地址0012h處置放一條Jump指令會怎樣？

這個過程不會停止下來，它會一直反覆執行下去！

我們需要這樣一種Jump指令，它只讓這個過程重複執行所需要的的次數，這種指令就是條件跳轉指令，怎麼實現它呢?我給出一種實現方式，簡單看看就好

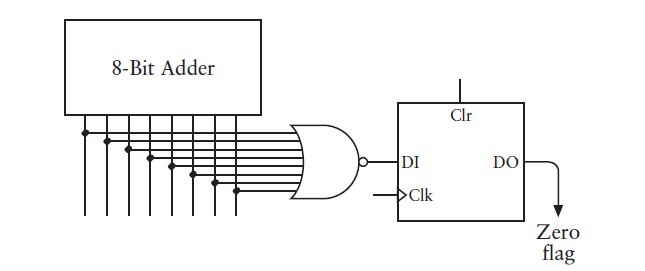
這種鎖存器叫零鎖存器，當8位加法器輸出為零時他鎖存的值才是1。有了進位鎖存器和零鎖存器以後，可以為指令表新增4條指令

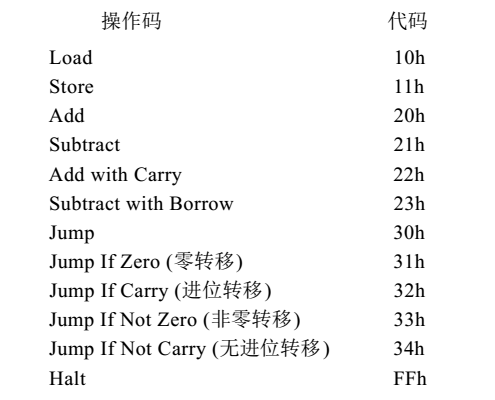
非零跳轉指令只有在零鎖存器輸出為0時才會跳轉到指定的地址，如果上一步的加法、減法、進位加法或者借位減法運算結果為0時，將不會發生跳轉。只需要在常規的跳轉命令的控制訊號之上再加一個控制訊號

那麼繼續剛才提出的問題，0012h地址之後的的指令為

Store指令不會影響零標誌位的值，只有Add、Subtract、Add with Carry、Subtract with borrow這些指令才能影響零標誌位的值，當執行到地28次迴圈時，1004h和1005h地址儲存的16位數等於A7和1Ch的乘積。1003h地址儲存的值為1，他和FFh相加的結果為0.零標誌位被置位！Jump If Not Zero指令不會再跳轉回到0000h地址處，程式執行完成。

現在可以說，我們這臺不斷完善的機器真的可以稱得上是一臺真正意義上的computer了！條件跳轉指令將計算器和計算機真正區分開來。

那麼，你現在明白了嗎，為什麼計算機能讀懂0和1？計算機和程式到底是什麼？

資料被附在電流上不斷地轉圈圈（迴圈的過程），當滿足某一條件之後，得到最終結果。

組合語言

把上述機器碼錶示成助記符的形式

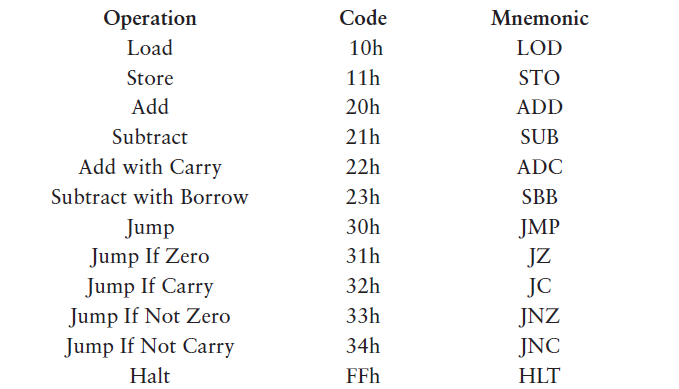
那麼這個乘法的程式可以寫成這種形式

編碼時最好不使用實際地址，用label來指代儲存器中的地址空間，所以上述程式可以改寫為

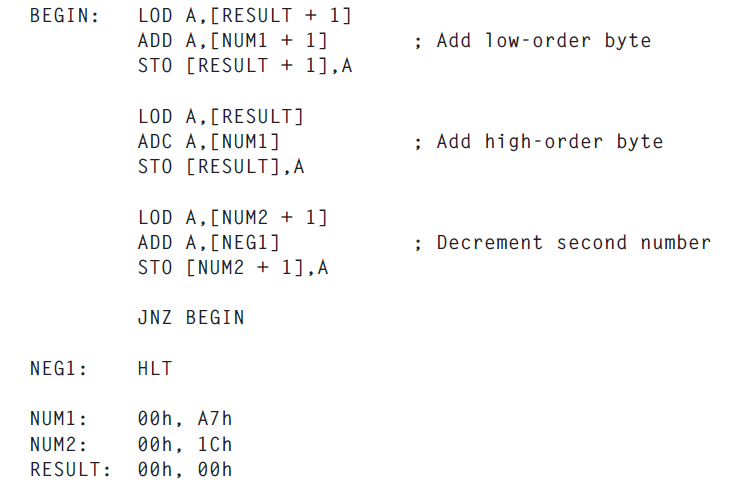
終於在春節到來之前寫完了，算是圓了自己的一份小小的心願。

寫的不好，歡迎大家批評改正。