B+樹和B樹的區別
一,b樹
b樹(balance tree)和b+樹應用在資料庫索引,可以認為是m叉的多路平衡查詢樹,但是從理論上講,二叉樹查詢速度和比較次數都是最小的,為什麼不用二叉樹呢?
因為我們要考慮磁碟IO的影響,它相對於記憶體來說是很慢的。資料庫索引是儲存在磁碟上的,當資料量大時,就不能把整個索引全部載入到記憶體了,只能逐一載入每一個磁碟頁(對應索引樹的節點)。所以我們要減少IO次數,對於樹來說,IO次數就是樹的高度,而“矮胖”就是b樹的特徵之一,它的每個節點最多包含m個孩子,m稱為b樹的階,m的大小取決於磁碟頁的大小。
█一個M階的b樹具有如下幾個特徵:
- 定義任意非葉子結點最多隻有M個兒子,且M>2;
- 根結點的兒子數為[2, M];
- 除根結點以外的非葉子結點的兒子數為[M/2, M],向上取整;
- 非葉子結點的關鍵字個數=兒子數-1;
- 所有葉子結點位於同一層;
- k個關鍵字把節點拆成k+1段,分別指向k+1個兒子,同時滿足查詢樹的大小關係。
█有關b樹的一些特性,注意與後面的b+樹區分:
- 關鍵字集合分佈在整顆樹中;
- 任何一個關鍵字出現且只出現在一個結點中;
- 搜尋有可能在非葉子結點結束;
- 其搜尋效能等價於在關鍵字全集內做一次二分查詢;
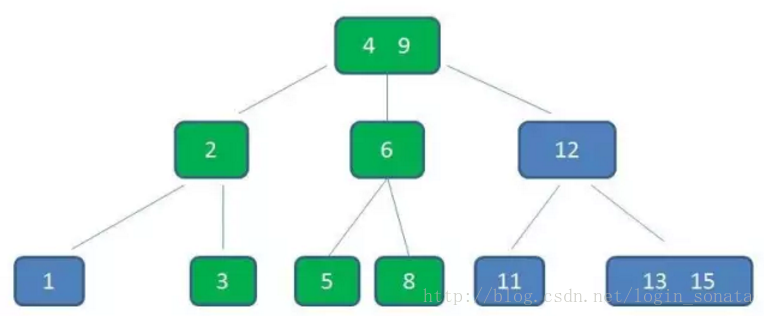
█如圖是一個3階b樹,順便講一下查詢元素5的過程:
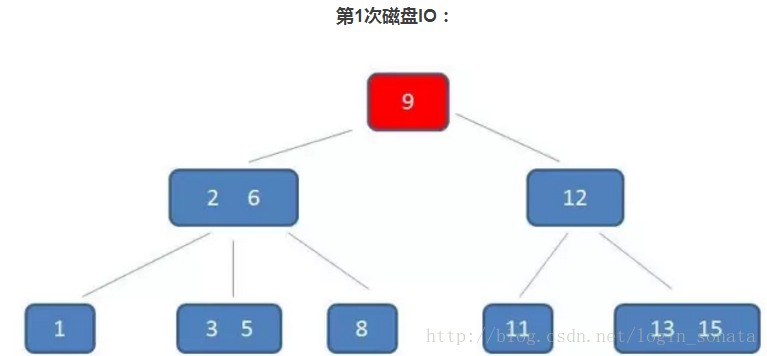
1,第一次磁碟IO,把9所在節點讀到記憶體,把目標數5和9比較,小,找小於9對應的節點;
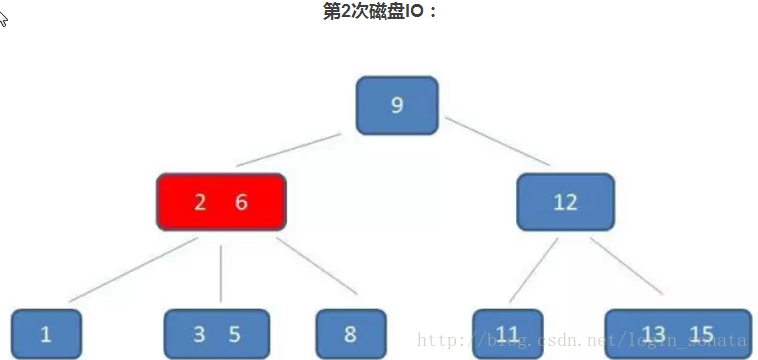
2,第二次磁碟IO,還是讀節點到記憶體,在記憶體中把5依次和2、6比較,定位到2、6中間區域對應的節點;
3,第三次磁碟IO就不上圖了,跟第二步一樣,然後就找到了目標5。
可以看到,b樹在查詢時的比較次數並不比二叉樹少,尤其是節點中的數非常多時,但是記憶體的比較速度非常快,耗時可以忽略,所以只要樹的高度低,IO少,就可以提高查詢效能,這是b樹的優勢之一。
█b樹的插入刪除元素操作:
比如我們要在下圖中插入元素4:
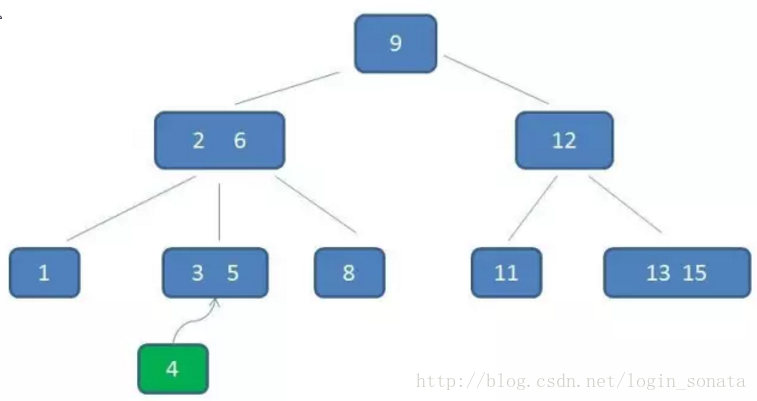
1,首先自頂向下查詢找到4應該在的位置,即3、5之間;
2,但是3階b樹的節點最多隻能有2個元素,所以把3、4、5裡面的中間元素4上移(中間元素上移是插入操作的關鍵);
3,上一層節點加入4之後也超載了,繼續中間元素上移的操作,現在根節點變成了4、9;
4,還要滿足查詢樹的性質,所以對元素進行調整以滿足大小關係,始終維持多路平衡也是b樹的優勢,最後變成這樣:
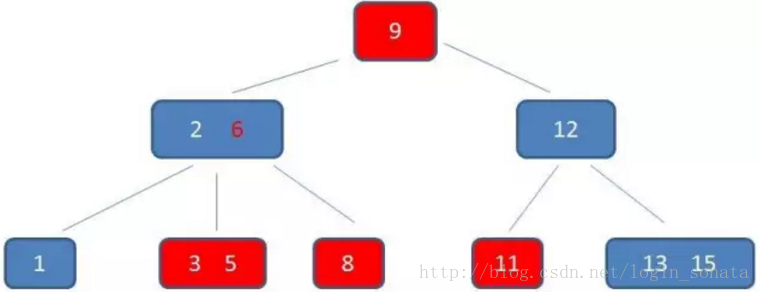
再比如我們要刪除元素11:
1,自頂向下查詢到11,刪掉它;
2,然後不滿足b樹的條件了,因為元素12所在的節點只有一個孩子了,所以我們要“左旋”,元素12下來,元素13上去:
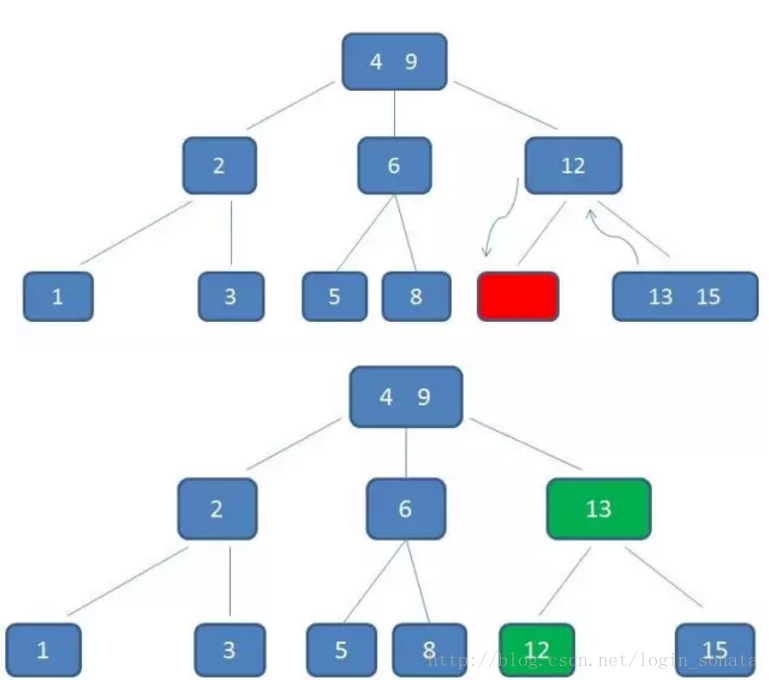
這時如果再刪除15呢?很簡單,當元素個數太少以至於不能再旋轉時,12直接上去就行了。
二,b+樹
b+樹,是b樹的一種變體,查詢效能更好。m階的b+樹的特徵:
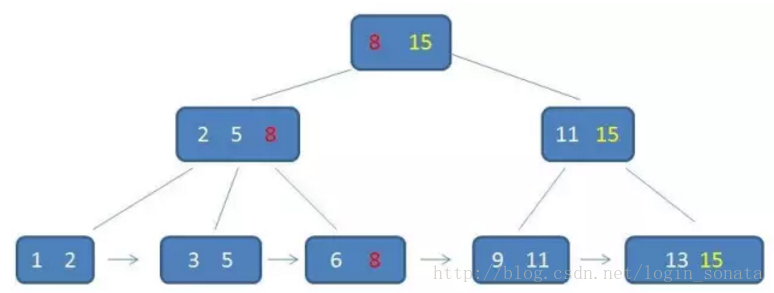
- 有n棵子樹的非葉子結點中含有n個關鍵字(b樹是n-1個),這些關鍵字不儲存資料,只用來索引,所有資料都儲存在葉子節點(b樹是每個關鍵字都儲存資料)。
- 所有的葉子結點中包含了全部關鍵字的資訊,及指向含這些關鍵字記錄的指標,且葉子結點本身依關鍵字的大小自小而大順序連結。
- 所有的非葉子結點可以看成是索引部分,結點中僅含其子樹中的最大(或最小)關鍵字。
- 通常在b+樹上有兩個頭指標,一個指向根結點,一個指向關鍵字最小的葉子結點。
- 同一個數字會在不同節點中重複出現,根節點的最大元素就是b+樹的最大元素。
█b+樹相比於b樹的查詢優勢:
- b+樹的中間節點不儲存資料,所以磁碟頁能容納更多節點元素,更“矮胖”;
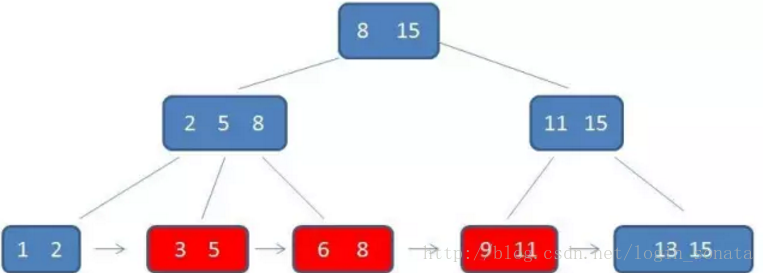
- b+樹查詢必須查詢到葉子節點,b樹只要匹配到即可不用管元素位置,因此b+樹查詢更穩定(並不慢);
- 對於範圍查詢來說,b+樹只需遍歷葉子節點連結串列即可,b樹卻需要重複地中序遍歷,如下兩圖: