多叉樹——B樹和B+樹
目錄
1 介紹
樹家族是為了實現方便快捷的查詢而存在的。樹的高度是命中查詢的一個不可抗拒的時間下限。在一定的資料條件下,樹的高度和寬度是相互制約的。對於二叉樹來說,雖然易於實現,卻沒有實際的價值。因為二叉樹的寬度固定,使樹的高度無法減小,因此出現了多叉樹。B樹、B+樹都屬於多叉樹。MySQL和Berkeley DB都是基於B樹原理而建立資料庫的。B樹是一種可實現的平衡多路查詢樹。
2 B樹
2.1 B樹的定義
B樹在維基百科是這麼定義的:“在電腦科學中,B樹(B-Tree)是一種樹狀資料結構,它能夠儲存資料,對其進行排序並允許以O(log n)的時間複雜度執行進行查詢、順序讀取、插入和刪除的資料結構。B樹,概括來說是一個節點可以擁有多於2個子節點的二叉排序樹。與自平衡二叉查詢樹不同,B-樹為系統最優化大塊資料的讀和寫操作。普遍運用在資料庫和檔案系統。”
B樹中所有節點的最大孩子節點數被稱為B樹的階,通常用m來表示。一棵m階B樹可以是一棵空樹,也可以是滿足一下條件的m叉樹。
1)每個節點最多有m個子結點,即每個節點最多有m-1個關鍵字;最少子節點要看是否為根節點,如果是非葉子節點的根節點,則至少要有2個節點,其他非根節點非葉節點至少要有[m/2]個節點,[m/2]表示m/2向上取整。
2)如果一個節點有n-1個關鍵字,則子節點有n個。這n-1個關鍵字按照遞增的順序排列。
3)每個節點的結構為:
| n | k1 | k2 |
.... | kn |
| p0 | p1 | p2 | ... | pn |
其中,n為節點中關鍵字的個數;ki為該節點的關鍵字且ki<k(i+1);pi為該節點的孩子節點指標
4)節點內關鍵字互不相等且按照從小到大順序排列。
5)葉子節點處於同一層;可以用空指標表示,是查詢失敗到達的位置。
5階B-樹例項:

2.2 B樹的查詢
B樹節點內的關鍵字是有序的,因此在節點內查詢時除了順序查詢還可以使用折半查詢。假設要查詢的關鍵字為key。步驟如下:
1)先讓key與根節點的關鍵字進行比較,如果key=k[i],則查詢成功;
2)若key<k[1],則到p[0]所指向的子節點進行查詢;
3)若key>k[n],則到p[1]所指向的子節點進行查詢;
4)若k[i]<key<k[i+1],則到p[i]所指向的子節點進行查詢;
5)若遇到空指標,則查詢失敗。
2.3 B樹的插入
在B樹插入key時,需要判斷key所在的節點的關鍵字的個數是否滿足多叉樹的條件。
2.4 B樹的刪除
2.5 B樹的應用
為了將大型資料庫檔案儲存在硬碟上,以減少訪問硬碟次數為目的,在此提出了一種平衡多路查詢樹——B-樹結構。由其效能分析可知它的檢索效率是相當高的 為了提高 B-樹效能’還有很多種B-樹的變型,力圖對B-樹進行改進,比如B+樹。
3 B+樹
3.1 定義
由於B樹的一個結點代表輔助的一個頁或者塊。一個節點到另一個節點的傳送要求一次耗時的頁交換,因此應該儘可能的減少節點訪問。(如果要求B樹中所有節點按升序列印,可以採用中序樹遍歷演算法,這是很容易實現。)但對非葉子節點,每次只能顯示一個鍵值,然後就得訪問另一頁。因此,應該改進B樹,以更快的方式順序訪問資料,而不是使用中序遍歷。B+樹解決了這個問題。B+樹的資料都儲存在葉子節點中,分支節點均為索引,因此B+樹用於資料庫索引,B樹適用於檔案索引。
B+樹和B樹的差異在於:
1)有m個子結點的的節點的關鍵字有m個;
2)非葉節點僅具有索引的作用,跟記錄有關的資訊均記錄在葉子結點中;
3)樹的所有葉子結點構成一個有序連結串列,可以按照關鍵碼排序的次序遍歷全部記錄。
相同點在於:
1)所有節點的子節點的個數最多為m;非葉根節點的子節點個數最少是2,非葉非根節點的子節點個數最少是[m/2];
2)所有葉子節點都在同一層。
4階B+樹例項:
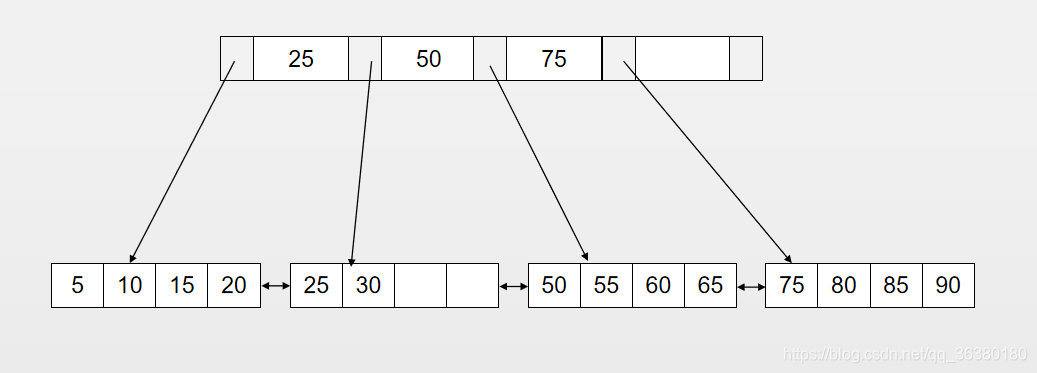
雙向連結串列,每頁可存放4條記錄。
3.2 B+樹的插入
| Leaf Page Full | Index Page Full | 操作 |
| no | no | 直接將記錄插入到葉節點 |
| yes | no | 1、拆分葉節點(Leaf Page) 2、將中間節點放入索引節點(Index Page) 3、小於中間節點的記錄放入左節點 4、大於等於中間節點的記錄放入右邊 |
| yes | yes | 1、拆分Leaf Page 2、小於中間節點的記錄放入左邊 3、大於等於中間節點的記錄放入右邊 4、拆分Index Page 5、小於中間節點的記錄放入左邊 6、大於等於中間節點的記錄放入右邊 6、將中間節點放入上一層Index Page |
為了保持平衡,對於新插入的鍵值可能會做多次拆頁操作(split),B+樹主要用於磁碟,多次拆頁意味著對磁碟多次操作,應該儘可能的減少對磁碟操作。因此B+樹提供了旋轉(rotation)操作。
旋轉發生在Leaf Page滿了但是左右兄弟節點還沒滿的情況下。通常情況下,左兄弟被首先檢查用來做旋轉操作。比如要插入70。
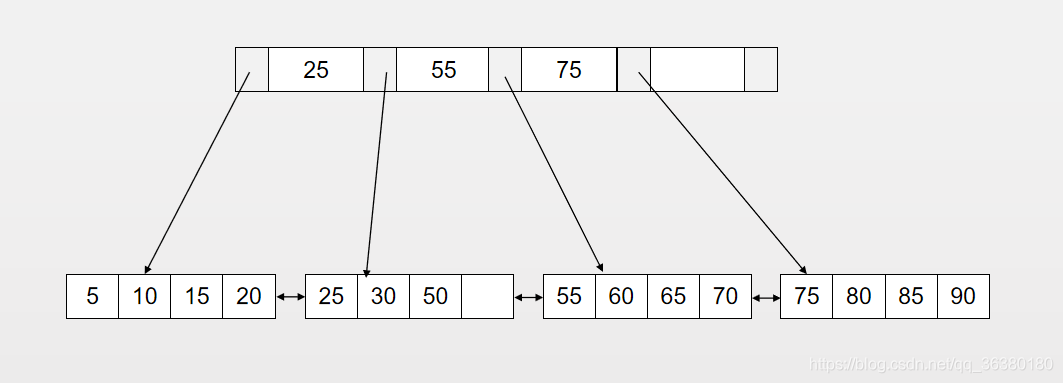
若按照拆頁操作則是:
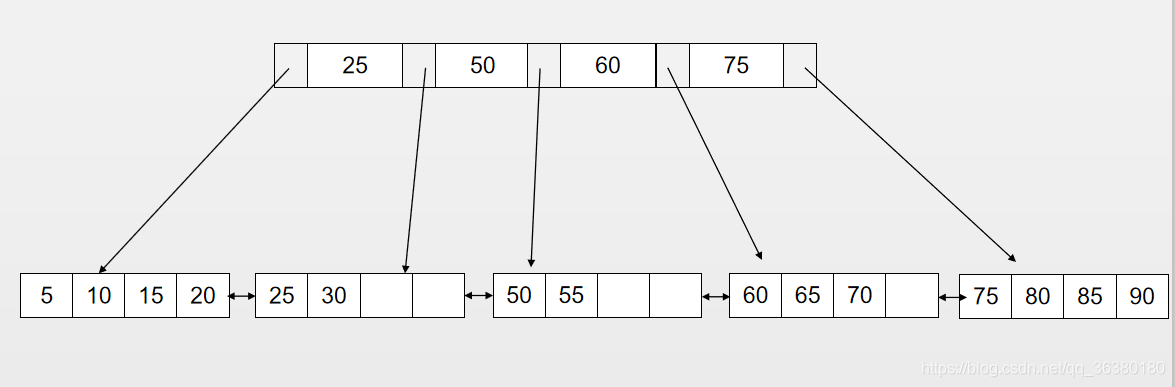
因此旋轉使得少了一次拆頁操作。
3.3 B+樹的刪除
B+樹使用填充因子(fill factor)來控制樹的刪除,50%是刪除因子可設的最小值,因為B+樹屬於多叉樹,要滿足多叉樹最小分支數的條件。
| Leaf Page Below Fill Factor | Index Page Below Fill Factor | 操作 |
| no | no | 直接刪除記錄,若該記錄還存在Index Page中,則更新Index Page |
| yes | no | 合併葉節點及兄弟節點,並更新Index Page |
| yes | yes | 1、合併葉節點及其兄弟節點 2、更新Index Page 3、合併Index Page及其兄弟節點 4、更新上一層Index Page |
