B+樹的概念不再贅述，偶然得到一題目，原題是在磁碟中進行樹的操作，應該是使用檔案偏移和定位那個幾個函式 ， 這裡簡單實現了B+樹在記憶體中的插入

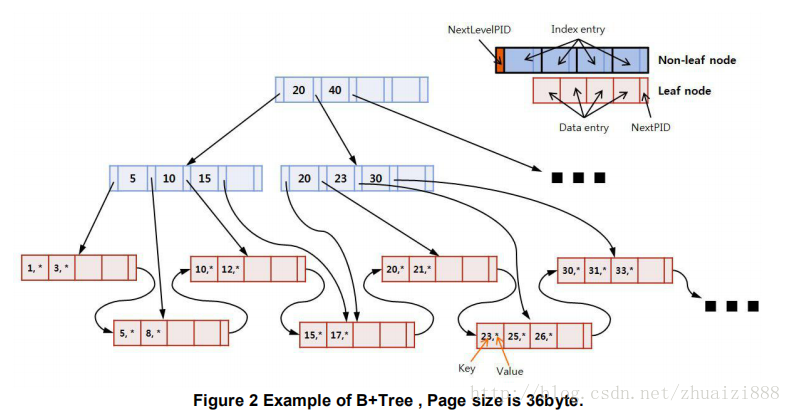
先看一下B+樹的結構：

定義了非葉子節點和葉子節點，NextLevelPid是指向子節點，IndexEntry中有索引，LeafNode是葉子節點，其中有資料Data和指向下一個葉子節點

class None_Leaf_Node;
struct Node
{
    int pid;

    None_Leaf_Node *fatherNode;
    virtual ~Node() {}

    virtual int getNodeEntrySize() { return
 
 0; }

};

struct None_Leaf_Node : public Node
{
    list<Node *> nextLevelNodes;
    list<int> keys;
    int getNodeEntrySize()
    {
        return keys.size();
    }

};

struct Leaf_Node : public Node
{
    map<int, int> keyValues;
    Leaf_Node *nextLeafNode;
    int getNodeEntrySize()
    {
        return
 
 keyValues.size();
    }
};

只實現了插入操作， 簡單理清一下思路：

1. 初次插入是從葉子節點，當葉子節點中的資料多於每個節點最大儲存數量，則分裂
2. 插入時需要尋找插入點，返回可以插入到的葉子節點
3. 分裂是一個遞迴的過程，從當前要分裂的點一直向上尋找父節點最後到根節點
4. 分裂時考慮父節點是否為空，如果為空new一個非葉子節點，當做根節點，儲存葉子節點
5. 有很多情況未測試，見諒

插入：

bool insert(int key, int rid)
    {
        //剛開始插入的幾次 直接在葉子節點插入
        if (typeid(*m_RootNode) == typeid
 
(Leaf_Node))
        {
            //向葉子節點插入
            auto itr =  dynamic_cast<Leaf_Node *>( m_RootNode) ->keyValues.insert(pair<int, int>(key, rid));
            if (itr.second)
            {
                cout << "插入成功" << endl;
            }
            else
            {
                cout << "插入失敗" << endl;
                return false;
            }

            //調整葉子節點
            adjustAfterInsert(m_RootNode, 1);
            return true;
        }
        else
        {
            //先查詢然後插入 
            Leaf_Node *lNode = findInsertPoint(key);
            if (lNode->fatherNode == nullptr)
            {
                return false;
            }

            auto itr = lNode->keyValues.insert(pair<int, int>(key, rid));
            if (itr.second)
            {
                cout << "插入成功" << endl;
            }
            else
            {
                cout << "插入失敗" << endl;
                return false;
            }
            adjustAfterInsert(lNode, 1);
            return true;
        }
    }

尋找插入點

Leaf_Node *findInsertPoint(int key) 
    {

        Node *curNode = m_RootNode;

        int depth = 1;
        //根節點是葉子節點,直接返回這個節點, 實際開發可以用一個標識標識葉子節點  非葉子節點 
        if (typeid(*curNode) == typeid(Leaf_Node))
        {
            return static_cast<Leaf_Node *>(curNode);
        }

        //根節點是非葉子節點 找到那個葉子節點

        while (depth <= m_Depth)
        {
            bool isLower = false;


                auto nextLevelNodesItr = static_cast<None_Leaf_Node *>(curNode)->nextLevelNodes.begin();

                for (const int &tempKey : static_cast<None_Leaf_Node *>(curNode)->keys)
                {
                    if (key < tempKey)
                    {
                        isLower = true;
                        curNode = *nextLevelNodesItr;
                        break;
                    }

                    nextLevelNodesItr++;

                }
                if (isLower == false)
                {
                    curNode = *nextLevelNodesItr;
                }


            depth++;
        }

        //處理葉子節點  depth == m_Depth
        return static_cast<Leaf_Node *>(curNode);

    }

插入後調整

void adjustAfterInsert(Node *node, uint32_t depth)
    {
        if (node->getNodeEntrySize() <= m_MaxEntryNum)
        {
            return;
        }

        if (depth > m_Depth)
        {
            m_Depth = depth;
        }

        //判斷是非葉子節點還是葉子節點 
        if (typeid(*node) == typeid(None_Leaf_Node))
        {
            None_Leaf_Node *curNode = static_cast<None_Leaf_Node *>(node);

            None_Leaf_Node *newNextNode = new None_Leaf_Node;
            newNextNode->fatherNode = curNode->fatherNode;



            //需要移動索引和子節點  
            auto childItr =  curNode->nextLevelNodes.begin();
            advance(childItr, 1);

            int count = 0;
            list<Node *>::iterator delChildItr;
            list<int>::iterator delKeyItr = curNode->keys.begin();
            for (const auto &curKey : curNode->keys)
            {
                if (count > m_MinEntryNum)
                {
                    if (newNextNode->keys.empty())
                    {
                        delChildItr = childItr;

                    }
                    //加入到新節點
                    newNextNode->keys.push_back(curKey);
                    newNextNode->nextLevelNodes.push_back(*childItr);
                }
                else
                {
                    delKeyItr++;
                }
                count++;
                childItr++;
            }

            //刪除原來的  
            curNode->keys.erase(delKeyItr, curNode->keys.end());
            curNode->nextLevelNodes.erase(delChildItr, curNode->nextLevelNodes.end());

            //調整父節點  父節點為空  當前是根節點
            if (curNode->fatherNode == nullptr)
            {
                None_Leaf_Node *newRootNode = new None_Leaf_Node;
                newRootNode->pid = 1;

                newRootNode->keys.push_back(*delKeyItr);
                newRootNode->nextLevelNodes.push_back(curNode);
                newRootNode->nextLevelNodes.push_back(newNextNode);

                //修改根節點
                m_RootNode = newRootNode;
                return;

            }
            else  
            {       
                auto itr = lower_bound(curNode->fatherNode->keys.begin(), curNode->fatherNode->keys.end(), *delKeyItr);

                //需要保證key 和  子節點的一致性  用set方便  
                curNode->fatherNode->keys.insert(itr, *delKeyItr);

                auto itr2 = curNode->fatherNode->nextLevelNodes.begin();


                for (; itr2 != curNode->fatherNode->nextLevelNodes.end(); itr2++)
                {
                    if (static_cast<Leaf_Node *>(*itr2)->keyValues.begin()->first == *delKeyItr)
                    {
                        itr2++;
                        break;
                    }
                }

                curNode->fatherNode->nextLevelNodes.insert(itr2, newNextNode);
                adjustAfterInsert(curNode->fatherNode, ++depth);
            }
        }
        else//葉子節點 
        {
            Leaf_Node *curNode = static_cast<Leaf_Node *>(node);
            Leaf_Node *nextLeafNode = new Leaf_Node();

            None_Leaf_Node *fatherNode = curNode->fatherNode;

            nextLeafNode->fatherNode = fatherNode;
            nextLeafNode->nextLeafNode = curNode->nextLeafNode;

            curNode->nextLeafNode = nextLeafNode;


            //分裂葉子節點
            int count = 1;
            int insertKey;
            for (const auto & itr : curNode->keyValues)
            {
                if (count > m_MinEntryNum)
                {       
                    if (nextLeafNode->keyValues.empty())
                    {
                        insertKey = itr.first;
                    }
                    nextLeafNode->keyValues.insert(itr);
                }
                count++;

            }

            //刪除原來的過半的  不可能有重複
            auto eraseItr = curNode->keyValues.lower_bound(insertKey);
            curNode->keyValues.erase(eraseItr, curNode->keyValues.end());


            int toInsertKey = nextLeafNode->keyValues.begin()->first;
            //修改父節點
            if (fatherNode == nullptr)
            {
                None_Leaf_Node *newRootNode = new None_Leaf_Node;


                newRootNode->keys.push_back(toInsertKey);
                newRootNode->nextLevelNodes.push_back(curNode);
                newRootNode->nextLevelNodes.push_back(nextLeafNode);

                curNode->fatherNode = newRootNode;
                nextLeafNode->fatherNode = newRootNode;

                //修改根節點
                m_RootNode = newRootNode;
            }
            else
            {
                //插入關鍵字和子節點
                //先找到插入點
                auto itr = lower_bound(fatherNode->keys.begin(), fatherNode->keys.end(), toInsertKey);
                //需要保證key 和  子節點的一致性  用set方便  
                fatherNode->keys.insert(itr, toInsertKey);


                //插入子節點， 用set  過載node運算子 更方便一些 
                auto itr2 = fatherNode->nextLevelNodes.begin();
                for (;itr2 != fatherNode->nextLevelNodes.end(); itr2++)
                {
                    if (static_cast<Leaf_Node *>(*itr2)->keyValues.begin()->first == toInsertKey)
                    {
                        itr2++;
                        break;
                    }
                }

                fatherNode->nextLevelNodes.insert(itr2, nextLeafNode);
                adjustAfterInsert(fatherNode, ++depth);
            }           
        }
    }