一、關係資料庫模型

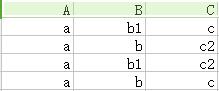
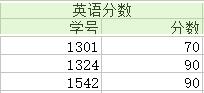
關係模型是一種基於表的資料模型，以下為關係學生資訊，該表有很多不足之處，本文研究內容就是如何改進它：

下面是一些重要術語：

1.屬性（attribute）：列的名字，上圖有學號、姓名、班級、興趣愛好、班主任、課程、授課主任、分數。

2.依賴（relation）：列屬性間存在的某種聯絡。

3.元組（tuple）：每一個行，如第二行 （1301，小明，13班，籃球，王老師，英語，趙英，70） 就是一個元組

4.表（table）：由多個屬性，以及眾多元組所表示的各個例項組成。

5.模式（schema）：這裡我們指邏輯結構，如 學生資訊（學號，姓名，班級，興趣愛好，班主任，課程，授課主任，分數）

6.域（domain）：資料型別，如string、integer等，上圖中每一個屬性都有它的資料型別（即域）。

7.鍵（key）：由關係的一個或多個屬性組成，任意兩個鍵相同的元組，所有屬性都相同。需要保證表示鍵的屬性最少。一個關係可以存在好幾種鍵，工程中一般從這些候選鍵中選出一個作為主鍵（primary key）。

8.候選鍵（prime attribute）：由關係的一個或多個屬性組成，候選鍵都具備鍵的特徵，都有資格成為主鍵。

9.超鍵（super key）：包含鍵的屬性集合，無需保證屬性集的最小化。每個鍵也是超鍵。可以認為是鍵的超集。

10.外來鍵（foreign key）：如果某一個關係A中的一個（組）屬性是另一個關係B的鍵，則該（組）屬性在A中稱為外來鍵。

11.主屬性（prime attribute）：所有候選鍵所包含的屬性都是主屬性。

12.投影（projection）：選取特定的列，如將關係學生資訊投影為學號、姓名即得到上表中僅包含學號、姓名的列

13.選擇（selection）：按照一定條件選取特定元組，如選擇上表中分數>80的元組。

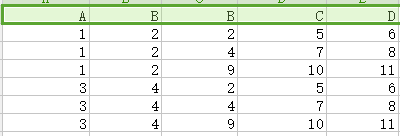
14.笛卡兒積（交叉連線Cross join）：如下圖，第一個關係每一行分別與第二個關係的每一行組合。

X=

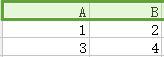
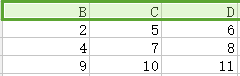
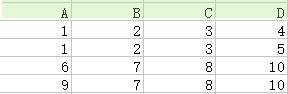
15.自然連線（natural join）：如下圖，第一個關係中每一行與第二個關係的每一行進行匹配，如果得到有交叉部分則合併，若無交叉部分則捨棄。

⋈=

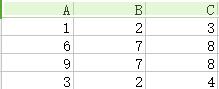
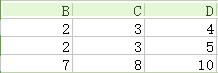
16.θ連線（theta join）：即加上約束條件的笛卡兒積，先得到笛卡兒積，然後根據約束條件刪除不滿足的元組。

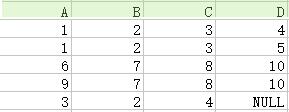
17.外連線（outer join）：執行自然連線後，將捨棄的部分也加入，並且匹配失敗處的屬性用NULL代替。

外連線=

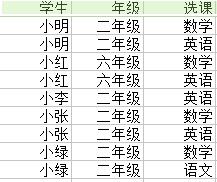
18.除法運算（division）：關係R除以關係S的結果為T，則T包含所有在R但不在S中的屬性，且T的元組與S的元組的所有組合在R中。下例足以說明，為了得到所有選了數學、英語並且是二年級的學生，我們用到除法運算。

除以=

二、函式依賴

1.函式依賴（functional dependency，FD）定義：

在一個關係中，任意元組，若屬性A1,A2....An一樣，則屬性B1,B2...Bm必一樣，那麼稱A1,A2...An函式決定B1,B2...Bm。

記號為    A1,A2...An → B1,B2...Bm     （Ai與Bi有函式依賴）

上圖中，若 學號 相同，則 姓名、班級、班主任 也必然相同，用這個道理我們可以粗略得出如下函式依賴：

學號 → 姓名，班級    （每一個學號對應一個姓名和班級，但由於可能重名，一個姓名不一定只對應一個學號）

班級 →班主任    （一個班級對應一個班主任，但我們不排除一個老師任兩個班的班主任，即一個班主任可能對應多個班級）

學號，課程→分數    （一個學號一個課程對應一個唯一的分數）

課程→ 授課主任    （一個課程對應一個授課主任）

授課主任→課程    （一個授課主任只能負責一門課程）

2.Armstrong aximos規則：

傳遞律（Transitivity）：R（A，B，C） 其中R為關係，ABC均為屬性。若A→B 和 B→C 則 A→C 。

增長律（Augmentation）：如果 A→B，則AC→BC，延長函式依賴不變。

自反律（Reflexivity）：如果 屬性集合B 屬於 屬性集合A，那麼 A→B，這個又稱為平凡函式依賴（見3）。

3.平凡函式依賴：

這裡的平凡（trivial）又有無價值、瑣碎的意思，理解上就是說了等於白說。

如 學號，姓名→學號 就是一個平凡函式依賴，因為右邊的屬於左邊的，屬於無價值資訊。

4.分解/結合規則：  

A1,A2...An→B1,B2...Bm 等效於 A1,A2...An→B1 ; A1,A2...An→B2 ; ..... A1,A2...An→Bm 。右邊是可以拆開、合併的。

5.屬性的閉包（closure）：

用一個例子來說明

已知關係的所有屬性集合{A,B,C,D,E,F}。

已知函式依賴  AB→C ， BC→AD ， D→E ， CF→B 。

求{A,B}的閉包  （我們用  {A,B}+  來表示）。

解：

<1>——分解函式依賴，使右邊只有一個屬性。 AB→C   ;   BC→A   ;   BC→D   ;   D→E   ;   CF→B 。

<2>——用{A,B}集合與這些函式依賴推匯出新的屬性加入集合，直到這個集合不再增長，此時該集合就是{A,B}+（閉包）。

容易發現 {A,B}+ = {A,B,C,D,E}。

實際上，求集合C的閉包C+，就是由全部函式依賴以及C，推匯出所有能夠推導的屬性集合 與 C的 並集。

閉包演算法能找到所有正確的函式依賴————反過來，已知 {A,B}，{A,B}+，我們就能列出所有能用{A,B}推匯出的函式依賴。

6.判定、計算鍵：

（1）運用閉包演算法判斷是否夠是鍵：

要驗證{A1,A2...An}是否是關係的鍵，可以先檢查“{A1,A2...An}+是否包含了關係的全部屬性”，再檢查“不存在從{A1,A2...An}中移出一個屬性後的集合C，使得C+包含關係的全部屬性”。

（2）圖解計算鍵：

用一個例子來說明

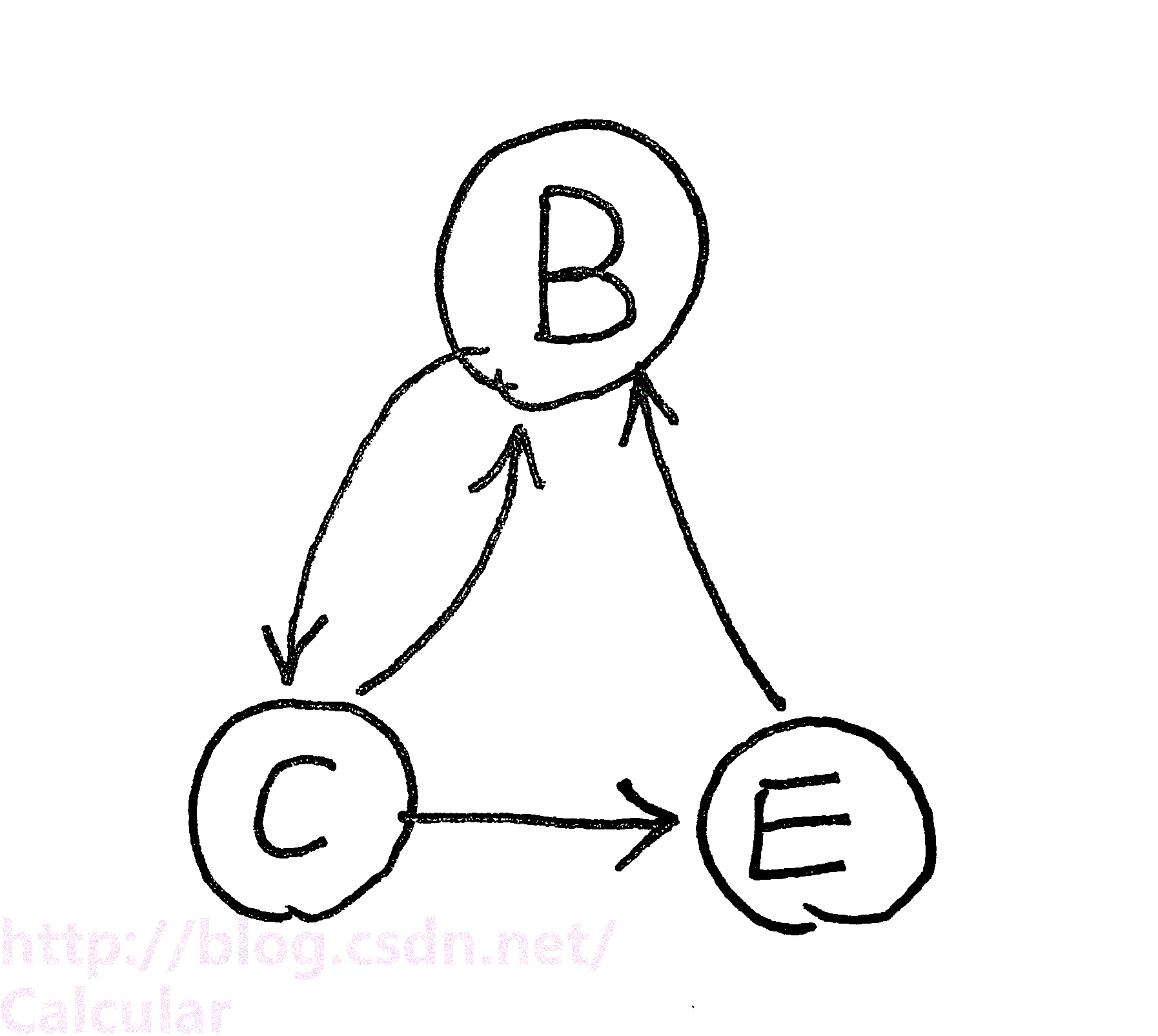
已知   {A,B,C,D,E}    :    AB→C ， B→D ， C→E ， CE→B

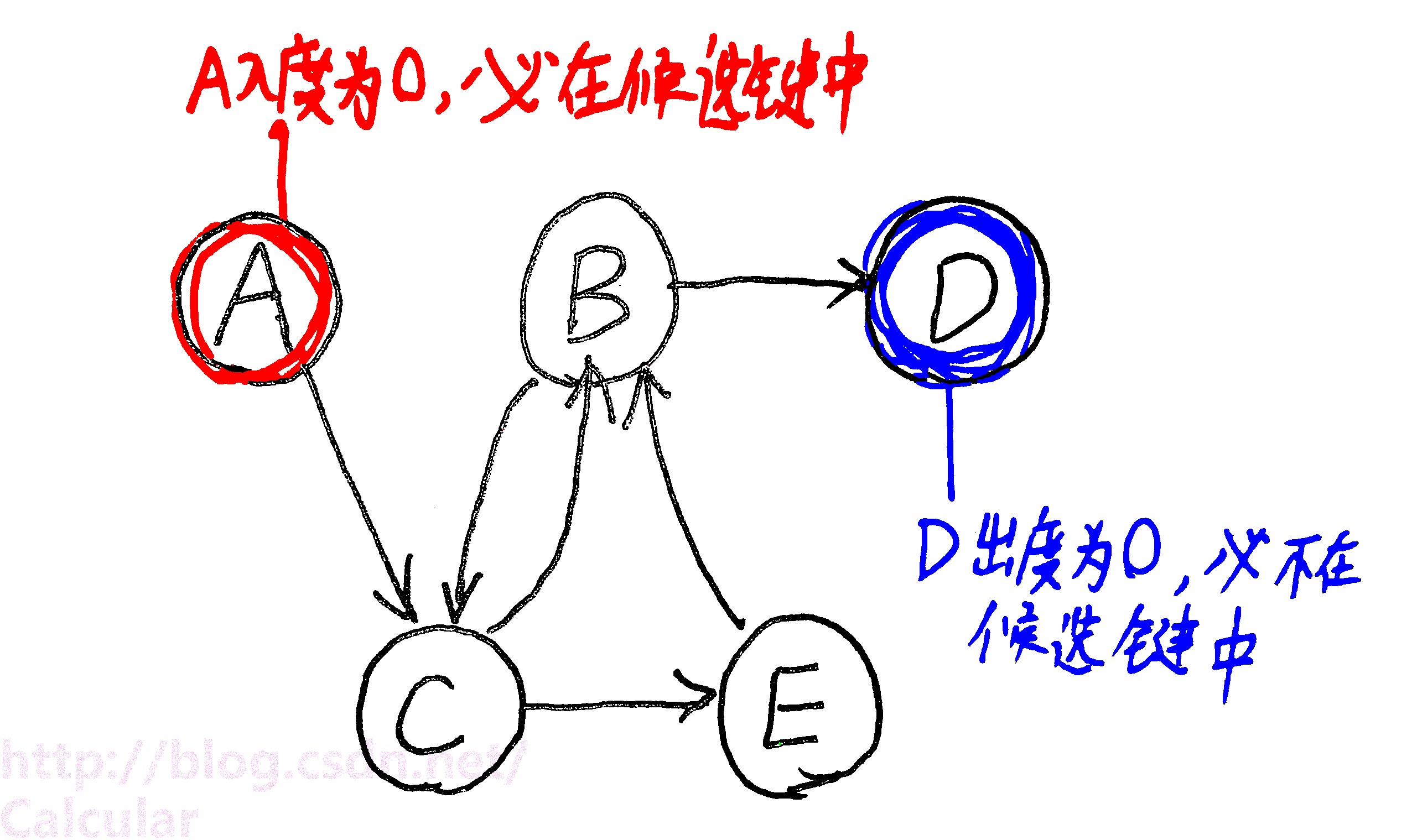
<1>——根據依賴關係畫出關係圖，入度為0的必在鍵中，出度為0的必不在鍵中，如下圖

現在可知，鍵中必有A，必無D。

<2>——將入度或出度為0結點刪去，化簡依賴圖，如下圖

<3>——選擇所有不能相互推導的屬性集合，逐一檢查能否遍歷上面的圖（注意，依賴圖中只有入度全滿足才算可推導）

上圖中不能相互推導的集合有：{B}能遍歷全圖，{C}能遍歷全圖，{E}不能遍歷全圖（單個E不能滿足B的全部入度）

（這裡，考慮一下{B,E}，因為從B出發能遍歷到E，連通，所以不檢查）

<4>——把上一步算出的集合分別與第1步中入度為0的點組合，最終得到候選鍵。

本例中候選鍵為 {A,B}、{A,C} 。

7.函式依賴的基本集：

（1）相關定義：

基本集：對於一個給定的函式依賴集合S，存在多個等效的函式依賴集合，任何與S等效的函式依賴集合都被稱為S的基本集。

最小化基本集（minimal basis）：需要滿足以下條件

（1）所有函式依賴的右邊均為單一屬性。（右邊最簡）

（2）刪除其中任何之一就不再是基本集。（數量最少）

（3）對於任意一個函式依賴，若其左邊刪除一個或多個屬性，則不再是基本集。（左邊最簡）

（2）計算最小化基本集：

用一個例子來說明

已知   {A,B,C,D,E}    :    AB→CD ， B→D ， C→E ， CE→B ， AC→B

<1>——首先把右邊都變成單一屬性

AB→C ， AB→D ， B→D ， C→E ， CE→B ， AC→B

<2>——對於每一個X→A，擬刪除，再看{X}+是否能得到A

檢查AB→C，擬刪除，計算{A,B}+ ={A,B,D}得不到C，保留。

檢查AB→D，擬刪除，計算{A,B}+ ={A,B,D,E}能得到D，刪除

刪除之後得到（AB→C ， B→D ， C→E ， CE→B ， AC→B）

檢查B→D，擬刪除，計算{B}+ ={B}得不到D，保留。

檢查C→E，擬刪除，計算{C}+ ={C}得不到E，保留。

檢查CE→B，擬刪除，計算{C,E}+ ={C,E}得不到B，保留。

檢查AC→B，擬刪除，計算{A,C}+ ={A,B,C,D,E}能得到B，刪除。

刪除之後得到（AB→C ， B→D ， C→E ， CE→B）

<3>——對於每一個X（X1,X2...）→A，依次檢查Xi，檢查{X-Xi}+是否能得到A，若能則用X-Xi取代X

檢查AB→C，{A}+={A}得不到C，{B}+={B,D}得不到C。

檢查CE→B，{C}+={C,E,B,D}能得到B，改為C→B。

因此最後得到最小化基本集為：AB→C ， B→D ， C→E ， C→B 。

8.投影函式依賴：

用一個例子來說明

已知關係R （A,B,C,D） 。

已知函式依賴 A→B   ;   B→C   ;   C→D 。

求函式依賴在屬性 (A,C,D) 上的投影（即刪除原來屬性B）。

解：

（1）求{A,C,D}所有子集的閉包，列出所涉及函式依賴（該函式依賴中只能出現A,C,D）：

{A}+ = {A,B,C,D}            :    A→C、A→D         (推匯出的，還有一個A→B因為涉及B直接丟棄）

{C}+ = {C,D}                  :    C→D

{D}+ = {D}                     :    無

{A,C}+ = {A,B,C,D}         :    與第一個涉及的函式依賴一樣

{A,D}+ ={A,B,C,D}          :    與第一個涉及的函式依賴一樣

{C,D}+ = {C,D}               :     無

{A,C,D}+ = {A,B,C,D}      :    與第一個涉及的函式依賴一樣

（2）最小化基本集：

A→C、A→D、C→D事實上已經是最小化基本集了，本例這個就是答案。

三、多值依賴

1.多值依賴（multivalued dependency，MVD）定義：

設R(U)是屬性集U上的一個關係模式，X,Y,Z是U的子集，並且Z=U-X-Y。關係模式R(U)中多值依賴 X→→Y 成立，即對於每一個(X,Z)有多個Y與之對應，並且Y的取值僅與X有關與Z無關。

多值依賴是兩個屬性或屬性集合之間相互獨立的宣言，我們可以認為當A→→B時，相同A下，（B）與（非A非B）相互獨立。

這裡有一個更淺顯的意思，即若A→→B，則A與B是一對相關項，A與（非A非B）也是一對相關項，B與（非A非B）是一對毫不相干的項（相關指存在某種聯絡），這樣也就解釋了為何對於每一個函式依賴同時也是多值依賴（唯一決定肯定是相關的），而每一個多值依賴不一定是函式依賴（相關不一定是唯一決定）。

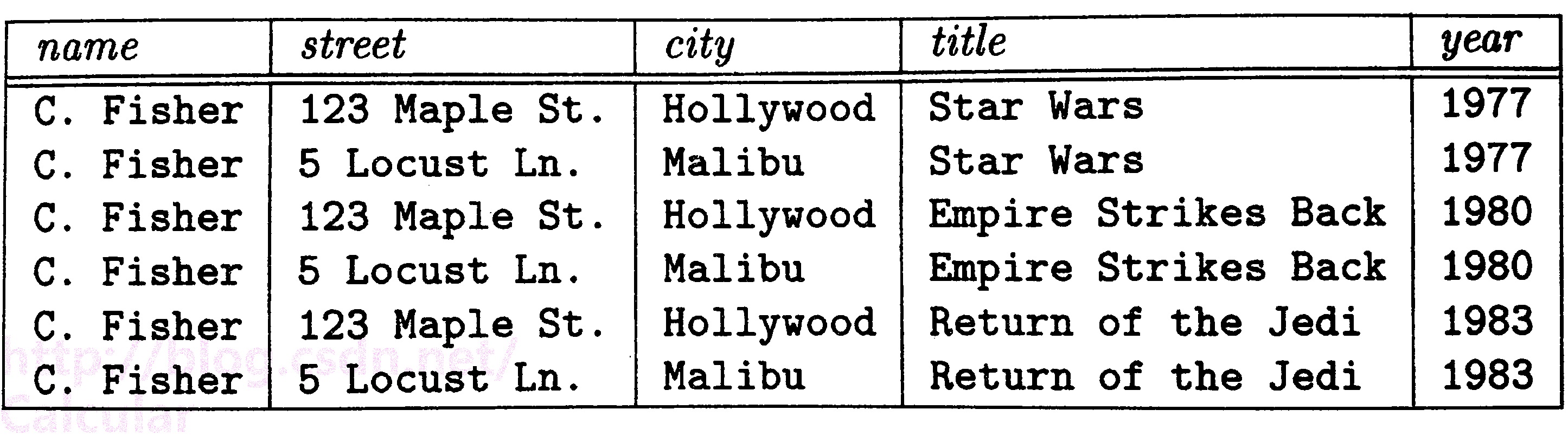
2.多值依賴的舉例：

上圖中，name表示一個明星的名字，street和city表示明星的住址（一個明星可以有好多住址），title和year表示該明星參演的某部電影的名字和上映時間。

對一個每一個確定的name與title,year，存在多個street,city，並且僅與name相關，或者說對於同一個明星他的住址與參演電影資訊是獨立的，因此可以推斷：

name→→street,city

name→→title,year    （實質上由於多值依賴的互補性，這兩者是等效的）

這種屬性之間的獨立性會產生冗餘，上圖中，每個地址出現了三次，每個電影也出現了兩次，我們需要一些方法消除多值依賴引起的冗餘（接下來會在第四正規化中提到）。

3.多值依賴的判別：

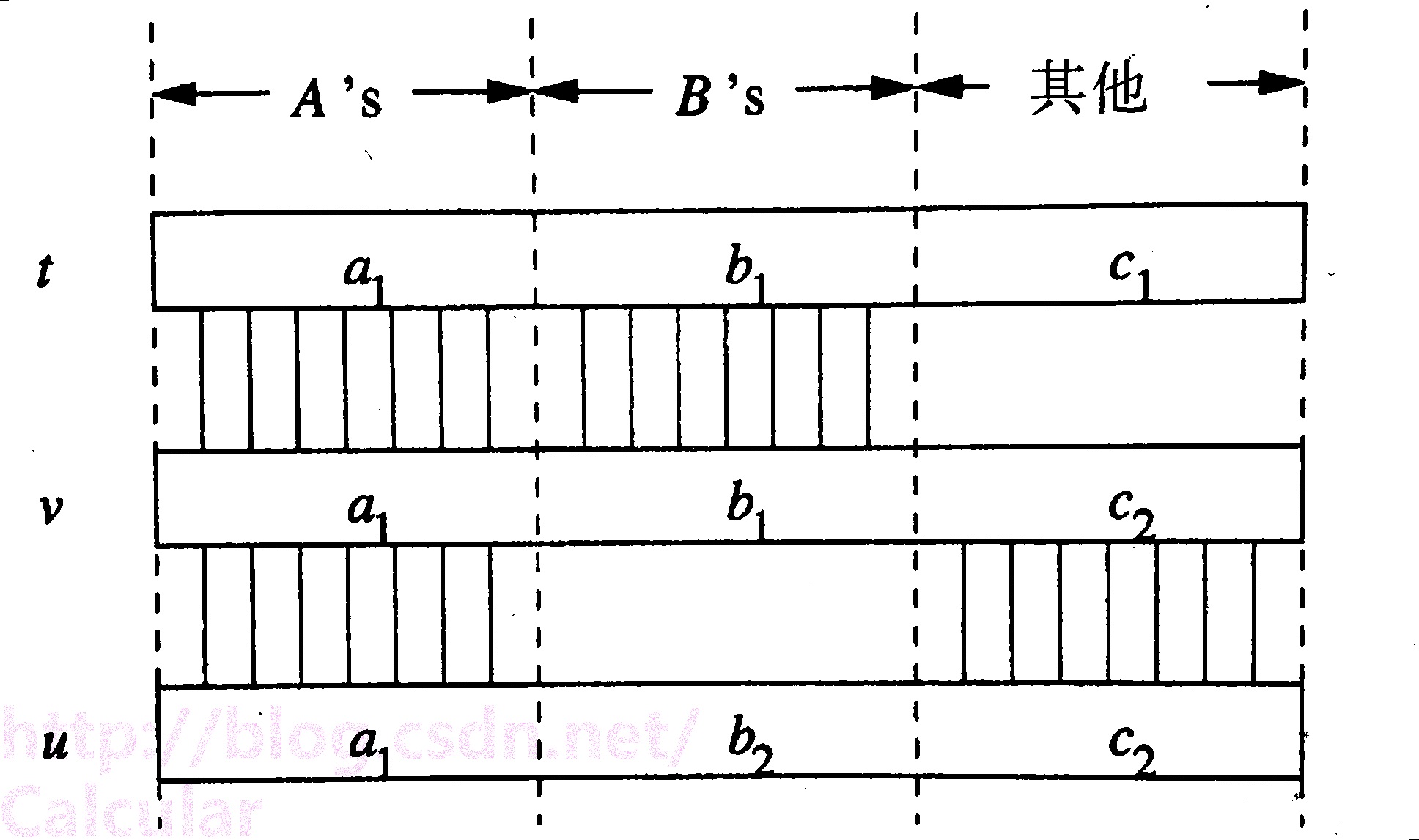
如果能在屬性A相同的情況下找到三個元組t、v、u，使

<1>——對於B屬性，v與t相同。(注：v與u可以不同可以相同，其實若B不屬於A肯定不同）

<2>——對於除了AB之外的其他屬性，v與u相同。(注：v與t可以不同可以相同，其實若B不屬於A肯定不同）

則   A→→B   （或者A→→非A非B，這是互補性的體現）。

4.多值依賴的規則（MVD為多值依賴的縮寫）：

（1）平凡MVD：和函式依賴一樣，例如    name,street→→street  只要右邊屬於左邊就一樣成立。

（2）傳遞規則：若X→→Y、Y→→Z 則 X→→Z-Y。（結果中除去Z中屬於Y的屬性）

（3）右邊不能分解：若name→→street,city 則不能分解成 name→→street 。

（4）FD推導MVD：若A1...An→B1...Bm（函式依賴），則必然A1...An→→B1...Bm（多值依賴）。

（5）互補規則（complementation rule）：若A→→B ，則 A→→非A非B 。

（6）附加平凡MVD：若某關係的所有屬性為{A1,A2...An,B1,B2...Bm}，則A1,A2...An→→B1,B2...Bm。

5.MVD發現演算法——chase擴充套件到MVD：

用一個例子來說明。

已知 {A,B,C,D}    :    A→B ， B→→C

需要證明：A→→C成立。

解：

這張初始化表只有兩行，兩行都填入有相同的屬性A，且不帶下標，然後

第一行：屬性C中填入不帶下標的，其餘空帶下標。

第二行：屬性（非A非C）中填不帶下標的，C中填帶下標的

<3>——根據多值依賴B→→C，找到B相同的兩行（其實只有兩行了），複製這兩行，並把這個副本中的C列對調，將其放到表的下面拼成一個四行的表，如下圖

只要出現全部無下標的一行（圖中第四行），則證明成立。

6.多值依賴的投影——應用MVD發現演算法：

用一個例子來說明

已知 R {A,B,C,D,E}    ：    A→→CD

問這個多值依賴是否蘊含著某些在S（A,B,C）上成立的依賴。

解：

首先根據上述多值依賴，很容易想到A→→C在S上成立（S沒有D屬性，因此去掉了），運用MVD發現演算法證明之。

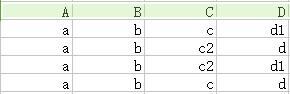
<1>——根據A→→C與S的屬性A,B,C構建初始化表，如下圖（參見MVD發現演算法）

<2>——根據多值依賴A→→CD，先複製兩行，將這個副本的CD兩列對調，再放到表下面，拼成一個四行的表。注意這個表沒有D列，就當它是空氣了，只要對調C列就行。如下圖

<3>——我們找到了沒有下標的行（第四行），證明成立。

四、關係資料庫模式設計要領

1.關係資料庫可能產生的異常（anmoaly）：

（1）冗餘（redundancy）：上圖關係中 學號、姓名、班級、興趣愛好、班主任、課程 、授課主任列中包含多個重複值。

（2）更新異常（update anomaly）：若更換了13班的班主任，僅僅更新第一行的資訊是不夠的，為此還要大費周折更新第二、三、四、五行的班主任資訊。

（3）刪除異常（deletion anomaly）：若小明英語缺考，我們需要刪除二、三行的全部資訊，但是同時也不必要地刪除了小明的跑步興趣愛好。

實際上，傳送異常的主要原因是，冗餘和關聯。

2.分解關係（decompose）：

為了消除上圖中的各種異常，我們將關係分解成六個，如下圖（注：分解都是按列分解的）

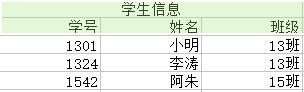
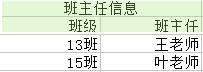
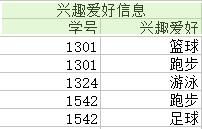
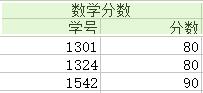
（1）對於冗餘：極大地減少了資料的重複次數，實際上已經消除到最佳。

（2）對於更新異常：若更換了13班的班主任，僅僅需要更新班主任資訊的第一行。

（3）對於刪除異常：若小明英語缺考，我們僅需要刪除英語分數的第一行。

3.分解的優略：