平衡多路查詢樹(B-Tree B+Tree)
B-tree就是我們常說的B樹,常常用於實現資料庫索引,因為它的查詢效率比較高
前面提到的2-3樹可以看作B樹的一種例項
一.為什麼不用二叉搜尋樹用B樹?
二叉查詢樹的時間複雜度是O(logN),查詢次數和比較次數較少,但是對於磁碟的IO次數,最壞情況下磁碟的IO次數由樹的高度決定,所以減少磁碟IO次數就必須壓縮樹的高度,讓瘦高的樹儘量變成矮胖的樹,這樣B樹就誕生了
二.B-tree
1.m階的B樹滿足以下性質:
(1)每個節點最多擁有m個子樹
(2)根節點最少有2個子樹
(3)分支節點最少擁有m/2棵子樹
(4)所有葉節點都在同一層,每個節點最多有m-1個key,並且以升序排列
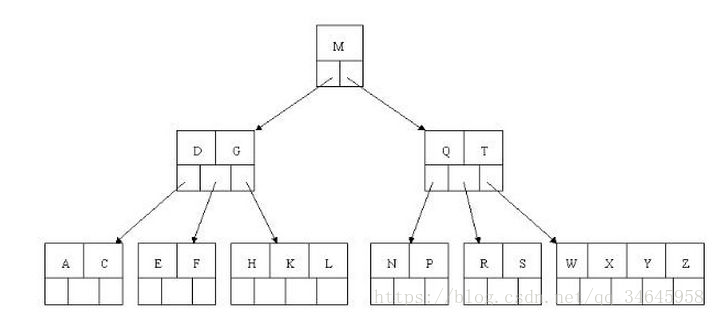
2.B樹查詢流程
(1)獲取根節點的關鍵字進行比較,當前根節點關鍵字為M,E要小於M(26個字母順序),所以往找到指向左邊的子節點(二分法規則,左小右大,左邊放小於當前節點值的子節點、右邊放大於當前節點值的子節點);
(2)拿到關鍵字D和G,D<E<G 所以直接找到D和G中間的節點;
(3)拿到E和F,因為E=E 所以直接返回關鍵字和指標資訊(如果樹結構裡面沒有包含所要查詢的節點則返回null);
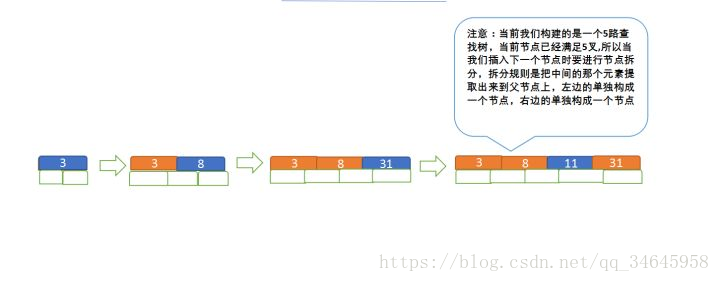
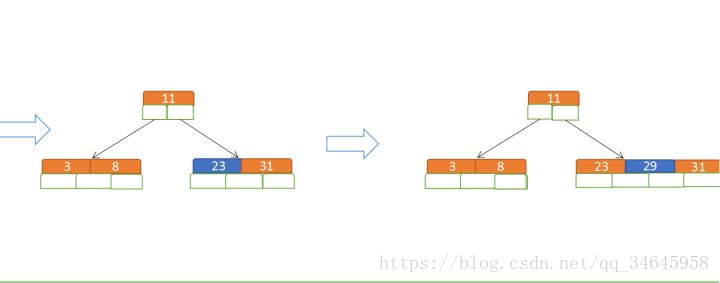
3、B樹的插入節點流程
定義一個5階樹(平衡5路查詢樹;),現在我們要把3、8、31、11、23、29、50、28 這些數字構建出一個5階樹出來;
遵循規則:
(1)當前是要組成一個5路查詢樹,那麼此時m=5,關鍵字數必須大於等於ceil(5/2) -1小於等於5-1(關鍵字數小於cei(5/2) -1就要進行節點合併,大於5-1就要進行節點拆分,非根節點關鍵字數>=2);
(2)滿足節點本身比左邊節點大,比右邊節點小的排序規則;
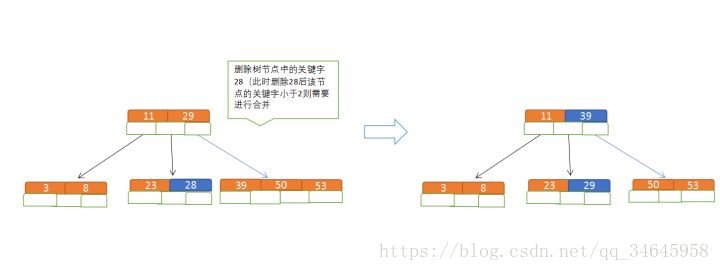
4.B樹節點的刪除
(1)當前是要組成一個5路查詢樹,那麼此時m=5,關鍵字數必須大於等於cei(5/2)-1,小於等於5-1,非根節點關鍵字數大於2;
(2)滿足節點本身比左邊節點大,比右邊節點小的排序規則;
(3)關鍵字數小於二時先從子節點取,子節點沒有符合條件時就向向父節點取,取中間值往父節點放;
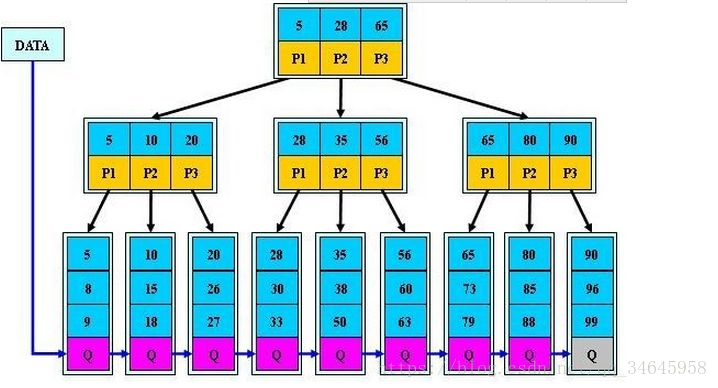
三.B+Tree
(1)B+跟B樹不同B+樹的非葉子節點不儲存關鍵字記錄的指標,這樣使得B+樹每個節點所能儲存的關鍵字大大增加;
(2)B+樹葉子節點儲存了父節點的所有關鍵字和關鍵字記錄的指標,每個葉子節點的關鍵字從小到大連結;
(3)B+樹的根節點關鍵字數量和其子節點個數相等;
(4)B+的非葉子節點只進行資料索引,不會存實際的關鍵字記錄的指標,所有資料地址必須要到葉子節點才能獲取到,所以每次資料查詢的次數都一樣;
特點:
在B樹的基礎上每個節點儲存的關鍵字數更多,樹的層級更少所以查詢資料更快,所有指關鍵字指標都存在葉子節點,所以每次查詢的次數都相同所以查詢速度更穩定;
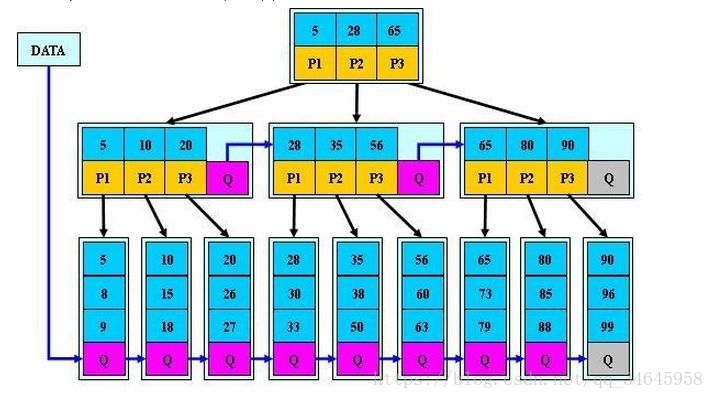
四.B*樹
B*樹是B+樹的變種,相對於B+樹他們的不同之處如下:
(1)首先是關鍵字個數限制問題,B+樹初始化的關鍵字初始化個數是cei(m/2),b*樹的初始化個數為(cei(2/3*m))
(2)B+樹節點滿時就會分裂,而B*樹節點滿時會檢查兄弟節點是否滿(因為每個節點都有指向兄弟的指標),如果兄弟節點未滿則向兄弟節點轉移關鍵字,如果兄弟節點已滿,則從當前節點和兄弟節點各拿出1/3的資料建立一個新的節點出來;
特點:
在B+樹的基礎上因其初始化的容量變大,使得節點空間使用率更高,而又存有兄弟節點的指標,可以向兄弟節點轉移關鍵字的特性使得B*樹額分解次數變得更少;
總結:從平衡二叉樹、B樹、B+樹、B*樹總體來看它們的貫徹的思想是相同的,都是採用二分法和資料平衡策略來提升查詢資料的速度;
不同點是他們一個一個在演變的過程中通過IO從磁碟讀取資料的原理進行一步步的演變,每一次演變都是為了讓節點的空間更合理的運用起來,從而使樹的層級減少達到快速查詢資料的目的;