【前言】

這個內容是重點，因為它涉及到資料庫的儲存方式，查詢效率等。

先埋坑，到時候有時間再填上去。

還有一篇文章，裡面詳細講述了刪除節點的幾種情況：

【勘誤】我推薦的第二篇文章針對需要合併操作的操作是錯誤
的，原因是作者沒有考慮到當父節點不夠數（譬如：5階數，關鍵字最少2個），當關鍵字數量為2時候，下撥一個數參與子節點之間的合併會破壞父節點的性質，所以，當出現合併操作時候，必須回溯父節點進行檢查，假如不符合性質，那麼必須遞迴合併。最壞的情況是一直到根節點都是不符合性質的，調整過後樹的高度減1。

【補充】大家假如看過我寫的紅黑樹的程式碼或者研讀過我推薦的兩篇文章，想必對紅黑樹的刪除操作有所認識。b樹的刪除也類

似，真正刪除的關鍵字必然是葉子層的關鍵字，其餘關鍵字我們可以通過調換來調整性質，一直到葉子層，假如有合併出現的話，記住需要回溯檢查調整父節點的性質。

假如各位對b樹的資訊不是很清楚的話，可以以上文章，只要用心去看一定能夠明白的。

下面我個人談一談感想什麼的，順便放出一個展示b樹的程式出來。

1、b樹的階m（最多包含的子樹數量），必須大於或等於2，最小為 [ceil(m / 2)]；

2、每個節點關鍵點最多為m-1，最少為 [ceil(m / 2)]-1：

3、各種操作介紹：

A、搜尋：從根節點開始遍歷，假如該節點包含關鍵字，返回真，否則，通過比較關鍵字與搜尋關鍵字的大小決定下一步需要遍歷的節點或葉，假如到葉還是沒有發現，那麼返回假。

B、插入關鍵字：先搜尋關鍵字，假如包含該關鍵字，則取消操作；否則，找到適合的葉子節點進行插入操作，假如插入關鍵字後該節點的關鍵字數量等於或大於m，那麼就進行分裂，回溯，上一個父節點等，有點複雜，下面會單獨用例子講解。

C、刪除關鍵字：先搜尋到關鍵字，確定所在節點，接著--這個需要待續，因為用肉眼刪除節點保持性質容易，但是用計算機來編寫程式難，，總之，刪除後必須保持樹的形狀，可以合併，也可以借用節點。後續看看是否有需要實現刪除操作。

經過反反覆覆除錯，尤其是對b樹插入的各種情況的調整，核心演算法終於得出正確答案了，現在先截圖說明演示軟體，然後下一篇將貼出演算法的核心實現。

【預設情形】

這裡設定5階子樹。

【插入關鍵字9】

【插入關鍵字12】

【插入關鍵字17】

【插入關鍵字19】

【插入關鍵字21】

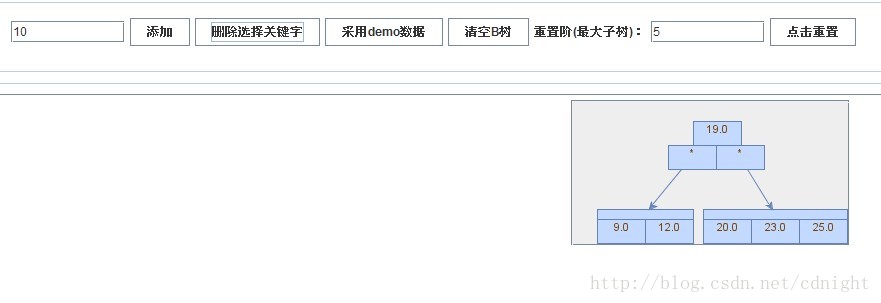
【插入關鍵字10】

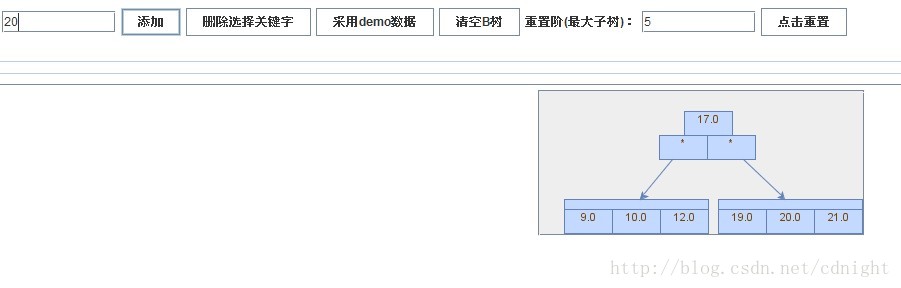
【插入關鍵字20】

【插入關鍵字24】

【插入關鍵字25】

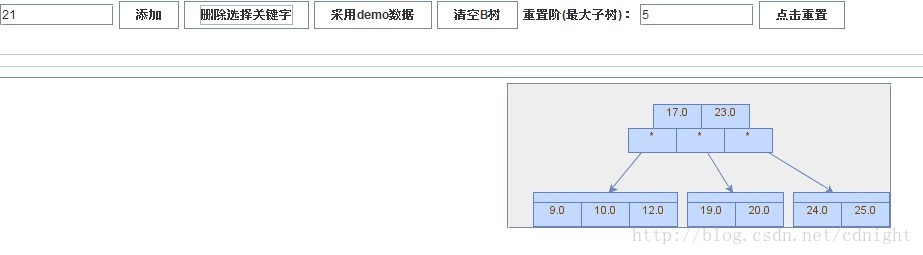
【插入關鍵字23】

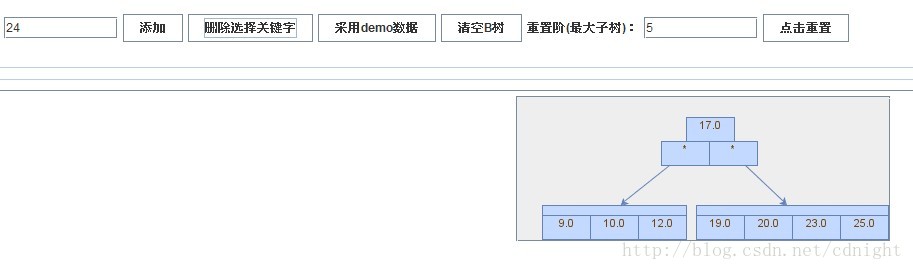
【刪除關鍵字21】

【刪除關鍵字24】

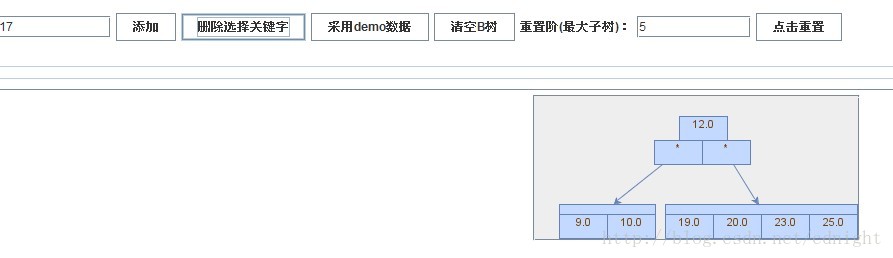
【刪除關鍵字17】

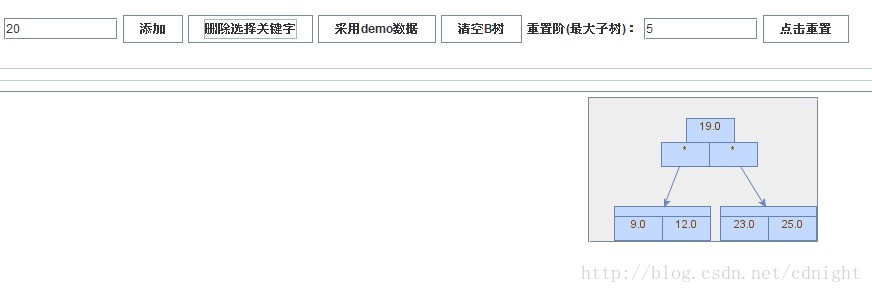
【刪除關鍵字10】

【刪除關鍵字105】

【刪除關鍵字19】

下面是這個試驗軟體的一個介面，裡面可以自定義階，也可以插入關鍵字，用了jgraphx開源庫，看起來還ok。

軟體下載地址：