平衡二叉樹的基本操作
一、平衡二叉樹的定義
"An algorithm for the organization of information"中發表了它。),它是二叉查詢樹的一種變體,除了滿足二叉查詢樹的性質之外還要滿足如下性質:①根節點的左子樹深度和右子樹的深度之差的絕對值小於2;②左子樹和右子樹也是一棵平衡二叉樹。平衡二叉樹又稱AVL樹(AVL樹得名於它的發明者 G.M. Adelson-Velsky 和 E.M. Landis,他們在1962年的論文
中依次插入節點K1<K2<K3<K4,那麼二叉查詢樹就退變成了連結串列,對連結串列的插入、刪除、查詢的操作時間為O(n), 然而對於平衡二叉樹的既然有了二叉查詢樹,為何又要發明平衡二叉樹?我們知道二叉查詢樹在插入操作的過程中,比如說要向二叉樹
二、AVL樹的基本操作
1、在介紹AVL樹的基本操作之前,我們先來看看AVL樹失衡的情況。
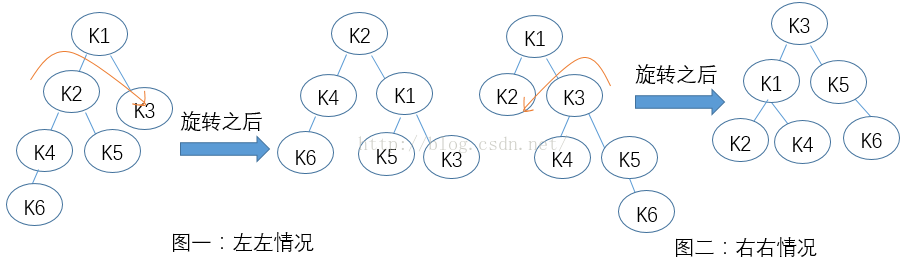
①左左情況:如圖一所示,K1的左子樹的高度與右子樹的高度之差為2,所以以K1位根節點的樹不是平衡二叉樹,K1為失衡的節點。以K1的左孩子K2為根的子樹,K2的左子樹的高度大於右孩子的高度,所以這樣失衡的樹為左左情況。我們通過旋轉來保持二叉樹的平衡性質。以K2為支撐柱,拿著節點K3順時針轉動,然後再調整各節點所指向的指標。
②右右情況:如圖二所示,其實右右情況與左左情況是映象對稱的。這裡就不再贅述,看圖就能明白一切。
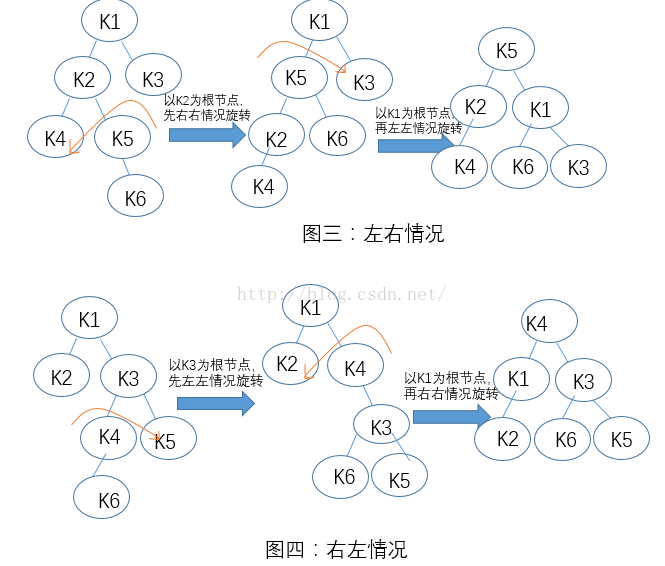
③左右情況:如圖三所示,K1的左子樹的高度與右子樹的高度之差為2,所以以K1位根節點的樹不是平衡二叉樹,K1為失衡的節點。以K1的左孩子K2為根的子樹,K2的右子樹的高度大於左孩子的高度,所以這樣失衡的樹為左右情況。我們先對K1的左子樹根K2進行右右情況的旋轉,然後再以K1為根進行左左情況旋轉,也就是進行雙旋轉。
④右左情況:如圖四所示,右左情況和左右情況是映象對稱的,這裡也不在贅述。
2、插入和刪除操作
平衡二叉樹的插入和刪除操作很有可能會改變平衡性質,這時我們就要對這棵非平衡的二叉樹進行旋轉操
作來保持其平衡性質。基本思路是這樣:如果是插入操作,因為插入到樹中的節點永遠是葉子節點,所以我們要沿著插入節點過程的逆方向來尋找最小失衡子樹;如果是刪除操作,刪除節點的左子樹有可能會成為非平衡最小二叉樹。當調整最小失衡子樹為平衡子樹時,不會影響其他平衡子樹的性質,當所有的最小失衡子樹調整為平衡子樹時,整個二叉樹也就是平衡二叉樹了。
3、程式碼
每行程式碼都有詳細的註釋,你可以通過加斷點除錯來驗證程式碼的正確性。#include <iostream> using namespace std; typedef int ElemType; /*節點結構*/ typedef struct node { ElemType key; struct node *parent, *lchid, *rchild; }BNode,*BTree; /*******************二叉樹的基本操作*****************************************/ /*獲取樹的高度*/ int get_depth(BTree root); /*判斷一棵樹是不是平衡二叉樹*/ bool isBanlace_tree(BTree root); /*平衡二叉樹的插入操作*/ bool insert_tree(BTree *root, ElemType e); /*平衡二叉樹的刪除操作*/ bool delete_tree(BTree *root, ElemType e); /*******************二叉樹的基本操作的一些輔助函式*******************************/ /*調整失衡的二叉樹,*root為刪除或新增的節點的指標*/ void keep_banlace(BTree *root, BTree check); /*當一棵樹不是平衡二叉樹的時候需要做的旋轉,root為失衡子樹的根節點*/ void LL_Rotate(BTree *root,BTree rotate);//情況一:左左情況 void RR_Rotate(BTree *root,BTree rotate);//情況二:右右情況 void LR_Rotate(BTree *root,BTree rotate);//情況三:左右情況 void RL_Rotate(BTree *root,BTree rotate);//情況四:右左情況 /*用節點v替換節點u*/ void replace_node(BTree *root, BTree u, BTree v); int main() { BTree root = NULL; insert_tree(&root, 5); insert_tree(&root, 4); insert_tree(&root, 3); insert_tree(&root, 2); insert_tree(&root, 1); insert_tree(&root, 6); insert_tree(&root, 7); insert_tree(&root, 8); delete_tree(&root, 2); delete_tree(&root, 1); if (isBanlace_tree(root)) { cout << "是平衡二叉樹" << endl; } else { cout << "不是平衡二叉樹" << endl; } } /*獲取樹的高度*/ int get_depth(BTree root) { if (root == NULL) return 0; int left, right, height; left = get_depth(root->lchid); right = get_depth(root->rchild); height = left > right ? (left +1) : (right+1);//樹的高度等於max(左子樹的高度,右子樹的高度)+1 return height; } /*根據平衡二叉樹的定義: 1、根節點的左子樹和右子樹的深度值差不能不大於1, 2、並且其左右子樹也是一顆平衡二叉樹*/ bool isBanlace_tree(BTree root) { if (root == NULL) return true; int left, right, diff; left = get_depth(root->lchid); right = get_depth(root->rchild); diff = left - right; if (diff > 1 || diff < -1) return false; return (isBanlace_tree(root->lchid) && isBanlace_tree(root->rchild)); } bool insert_tree(BTree *root, ElemType e) { /*構造並初始化節點*/ BTree temp = (BTree)malloc(sizeof(BNode)); temp->parent = NULL; temp->lchid = NULL; temp->rchild = NULL; temp->key = e; /*為空樹則直接插入*/ if (*root == NULL) { *root = temp; return true; } /*不為空樹,在插入的過程中需要保持平衡*/ BTree x = *root; BTree y = x; while (x != NULL && x->key != e) { y = x; if (x->key > e) x = x->lchid; else x = x->rchild; } if (x != NULL)//說明樹中存在相等的key return false; if (y->key > e) y->lchid = temp; else y->rchild = temp; temp->parent = y; keep_banlace(root, temp->parent); return true; } /*平衡二叉樹的刪除操作: 1、刪除的節點沒有孩子節點 2、刪除的節點只有一個孩子節點 3、刪除的節點有兩個孩子節點*/ bool delete_tree(BTree *root, ElemType e) { BTree x;//用來儲存指向有可能會是最小非平衡子樹的根節點 BTree temp = *root; /*找到要刪除的節點*/ while (temp != NULL && temp->key != e) { if (temp->key > e) temp = temp->lchid; else temp = temp->rchild; } if (temp == NULL)//沒有找到該節點 return 0; /*刪除的節點有兩個孩子節點*/ BTree y; if (temp->lchid != NULL && temp->rchild != NULL) { /*找z的後繼y*/ y = temp->rchild; while (y->lchid != NULL) y = y->lchid; if (y == temp->rchild)//節點y是z的左孩子 { replace_node(root, temp, y); y->lchid = temp->lchid; temp->lchid->parent = y; /*如果是這種情況那麼在刪除後,以z->parent為根節點的樹可能會成為最小非平衡子樹*/ x = temp->parent; } else { replace_node(root, y, y->rchild); replace_node(root, temp, y); y->lchid = temp->lchid; temp->lchid->parent = y; y->rchild = temp->rchild; temp->rchild->parent = y; /*如果是這種情況那麼在刪除後,以z->rchild為樹根的樹的左子樹的高度會降低,有可能會成為最小非平衡子樹*/ x = temp->rchild; } } /*有一個孩子節點*/ else if (temp->lchid != NULL || temp->rchild != NULL) { if (temp->lchid != NULL) replace_node(root, temp, temp->lchid); else replace_node(root, temp, temp->rchild); /*如果是這種情況那麼在刪除後,以z->parent為根節點的樹可能會成為最小非平衡子樹*/ x = temp->parent; } /*沒有孩子節點*/ else { replace_node(root, temp, NULL); /*如果是這種情況那麼在刪除後,以z->parent為根節點的樹可能會成為最小非平衡子樹*/ x = temp->parent; } /*完成刪除之後,我們要保持刪除之後的樹任然為平衡二叉樹*/ keep_banlace(root,x); free(temp); return true; } /*調整失衡的二叉樹: 首先在插入(或刪除)新結點處沿著樹向上找到失去平衡的最小子樹根結點的指標。 然後再調整這個子樹中有關結點之間的連結關係,使之成為新的平衡子樹。 當失去平衡的最小子樹被調整為平衡子樹後,原有其他所有平衡子樹無需調整, 整個二叉排序樹就又成為一棵平衡二叉樹。*/ void keep_banlace(BTree *root,BTree check) { int left, right, diff; while (check != NULL)//從check節點開始檢查是否為平衡二叉樹 { left = get_depth( check->lchid); right = get_depth(check->rchild); diff = left - right; if (diff > 1 || diff < -1)//不是平衡二叉樹 { if (diff > 1) { /*左左情況*/ if (get_depth(check->lchid->lchid) > get_depth(check->lchid->rchild)) { LL_Rotate(root,check); } else//左右情況 { RR_Rotate(root,check); LL_Rotate(root,check); } } else { /*右右情況*/ if (get_depth(check->rchild->rchild) > get_depth(check->rchild->lchid)) { RR_Rotate(root,check); } else { LL_Rotate(root,check); RR_Rotate(root,check); } } check = check->parent->parent; } else check = check->parent; } } /*情況一:左左情況 失衡節點的左子樹高度-左子樹高度>1 失衡節點的左孩子的左子樹高度大於失衡節點的左孩子的右子樹高度 */ void LL_Rotate(BTree *root, BTree rotate) { BTree temp = rotate->lchid; if (rotate->parent == NULL) { *root = temp; } else { if (rotate->parent->lchid == rotate) rotate->parent->lchid = temp; else rotate->parent->rchild = temp; } temp->parent = rotate->parent; rotate->parent = temp; rotate->lchid = temp->rchild; temp->rchild = rotate; } void RR_Rotate(BTree *root, BTree rotate)//情況二:右右情況,與情況一是映象的 { BTree temp = rotate->rchild; if (rotate->parent == NULL) { *root = temp; } else { if (rotate->parent->lchid == rotate) rotate->parent->lchid = temp; else rotate->parent->rchild = temp; } temp->parent = rotate->parent; rotate->parent = temp; rotate->rchild = temp->lchid; temp->lchid = rotate; } /*情況三:左右情況 失衡節點的左子樹高度-左子樹高度>1 失衡節點的左孩子的左子樹高度小於失衡節點的左孩子的右子樹高度*/ void LR_Rotate(BTree *root, BTree rotate)//情況三:左右情況 { /*先右右情況的旋轉*/ RR_Rotate(root,rotate->lchid); /*再左左情況的旋轉*/ LL_Rotate(root,rotate); } void RL_Rotate(BTree *root, BTree rotate)//情況四:右左情況,與情況三映象對稱 { /*先左左情況的旋轉*/ LL_Rotate(root,rotate->rchild); /*再右右情況的旋轉*/ RR_Rotate(root, rotate); } /*用節點v替換節點u*/ void replace_node(BTree *root, BTree u, BTree v) { if (u->parent == NULL) *root = v; else if (u == u->parent->lchid) u->parent->lchid = v; else u->parent->rchild = v; if (v != NULL) v->parent = u->parent; }