線索二叉樹的實現(C語言)
阿新 • • 發佈:2018-12-25
概念
鑑於普通二叉樹使用過程中會出現空間的浪費,後人對在在二叉樹的的基礎上做了改進,利用它的空指標域存放在某種遍歷次序下指向它的前驅結點,和後繼結點的指標。這些指標稱為線索,相應的二叉樹就成了線索二叉樹。
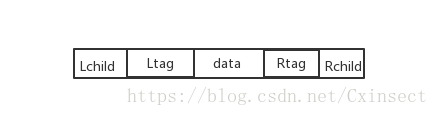
結點結構
- Ltag為0時指向該結點的左孩子,為1時指向該結點的前驅。
- Rtag為0時指向該結點的右孩子,為1時指向該結點的後繼。
結構實現
線索儲存結構定義
typedef enum {Link,Thread} PointerTag; //定義線索
typedef struct BithrNode{
char data; //結點資料 樹的線索化
樹的線索化過程其實就是遍歷過程中修改空指標域,因為此時當前結點的後繼還沒有訪問到,只能對它的前驅結點進行判斷,所以用一個全域性變數來儲存該結點的前驅結點,完成後續結點線索化。
BiThrTree pre; //定義全域性變數,儲存前驅結點 中序遍歷線索化過程
void InThreading(BiThrTree T)
{
if( T ) //判斷根結點是否為空
{
InThreading(T->pLchild); //遞迴左子樹線索
if (!T->pLchild) //左子樹為空
{
T->Ltag = Thread; //前驅線索
T-> 為了和雙向連結串列一樣,從根結點或者是尾結點都能訪問整個樹當中的資料,我們可以定義一個頭結點,(a)讓頭結點的左指標域指向根結點,(b)右指標域指向中序遍歷的最後一個結點。(c)讓中序遍歷的第一個結點的左指標域指向頭結點,(d)最後一個結點的右指標域指向頭結點。
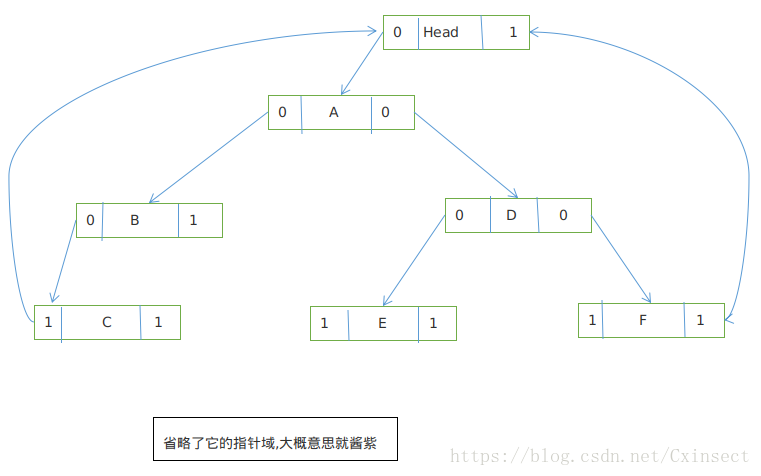
程式碼如下
- 其中p是頭指標,t是根結點
void InOrdThreading(BiThrTree *p,BiThrTree t)
{
*p = (BiThrTree)malloc(sizeof(BiThrNode)); //為頭結點分配空間
if((*p) == NULL)
{
printf("記憶體分配失敗\n");
exit(1);
}
(*p)->Ltag = Link;
(*p)->Rtag = Thread; //後繼線索線索
(*p)->pRchild = *p; //右指標域先指向自身
if(!t) //判斷根結點是否為空
(*p)->pLchild = *p; //為空頭結點左指標域指向自身
else{
(*p)->pLchild = t; //不空指向根結點
pre = *p; //初始化前驅結點
InThreading(t); //線索化過程
pre->pRchild = *p; //完成(b)過程
pre->Rtag = Thread; //後繼線索化
(*p)->pRchild = pre; //完成(d)過程
}
return;
}遍歷輸出
- 其中p是頭結點,T是根結點
void InOrderTraverse(BiThrTree p)
{
BiThrTree T;
T = p->pLchild;
while( p!=T) //空樹或者遍歷結束時
{
while(T->Ltag == Link) // 當Link等於0時迴圈到中序序列第一個結點
T = T->pLchild;
printf("%c\t",T->data); //列印資料
while(T->Rtag == Thread && T->pRchild != p)
{
T = T->pRchild;
printf("%c\t",T->data);
}
T = T->pRchild; //T遞進至右子樹根
}
printf("\n");
return;
} 輸入
輸出
樹的建立採用前序遍歷遞迴的方式建立,本篇文章不再贅述。
有問題歡迎指正。