詳解二叉查詢樹演算法的實現(c語言)
樹(Tree)是n(n≥0)個結點的有限集。在任意一棵非空樹中:(1)有且僅有一個特定的被稱為根(Root)的結點;(2)當n>1時,其餘結點可分為m(m>0)個互不相交的有限集T1,T2,…,Tm,其中每一個集合本身又是一棵樹,並且稱為根的子樹(SubTree)。
結點擁有的子樹數稱為結點的度(Degree)。度為0的結點稱為葉子(Leaf)或終端結點。度不為0的結點稱為非終端結點或分支結點。
樹的度是樹內各結點的度的最大值。
結點的子樹的根稱為該結點的孩子(Child),相應地,該結點稱為孩子的雙親(Parent)。
結點的層次(Level)是從根結點開始計算起,根為第一層,根的孩子為第二層,依次類推。樹中結點的最大層次稱為樹的深度(Depth)或高度。
如果將樹中結點的各子樹看成從左至右是有次序的(即不能互換),則稱該樹為有序樹,否則稱為無序樹。
1、二叉樹
二叉樹(Binary Tree)的特點是每個結點至多具有兩棵子樹(即在二叉樹中不存在度大於2的結點),並且子樹之間有左右之分。
二叉樹的性質:
(1)、在二叉樹的第i層上至多有2i-1個結點(i≥1)。
(2)、深度為k的二叉樹至多有2k-1個結點(k≥1)。
(3)、對任何一棵二叉樹,如果其終端結點數為n0,度為2的結點數為n2,則n0=n2+1。
一棵深度為k且有2k-1個結點的二叉樹稱為滿二叉樹。
可以對滿二叉樹的結點進行連續編號,約定編號從根結點起,自上而下,自左至右,則由此可引出完全二叉樹的定義。深度為k且有n個結點的二叉樹,當且僅當其每一個結點都與深度為k的滿二叉樹中編號從1到n的結點一一對應時,稱之為完全二叉樹。
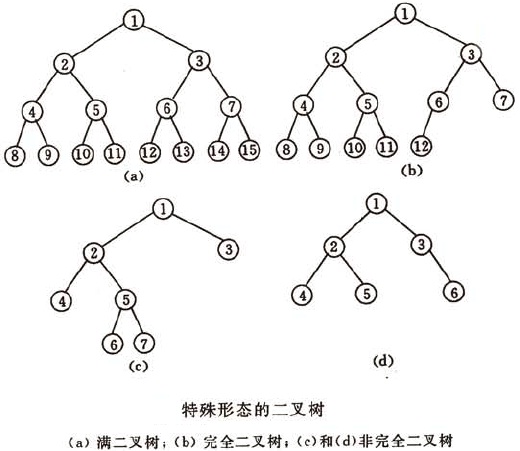
(4)、具有n個結點的完全二叉樹的深度為不大於log2n的最大整數加1。
(5)、如果對一棵有n個結點的完全二叉樹的結點按層序編號(從第1層到最後一層,每層從左到右),則對任一結點i(1≤i≤n),有
a、如果i=1,則結點i是二叉樹的根,無雙親;如果i>1,則其雙親是結點x(其中x是不大於i/2的最大整數)。
b、如果2i>n,則結點i無左孩子(結點i為葉子結點);否則其左孩子是結點2i。
c、如果2i+1>n,則結點i無右孩子;否則其右孩子是結點2i+1。
二叉樹的鏈式儲存:
鏈式二叉樹中的每個結點至少需要包含三個域,資料域和左、右指標域。

二叉樹的遍歷:
假如以L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹,則可有DLR、DRL、LRD、LDR、RLD、RDL這六種遍歷二叉樹的方案。若限定先左後右,則只有三種方案,分別稱之為先(根)序遍歷、中(根)序遍歷和後(根)序遍歷,它們以訪問根結點的次序來區分。
2、二叉查詢樹
二叉查詢樹(BinarySearch Tree,也叫二叉搜尋樹,或稱二叉排序樹Binary Sort Tree)或者是一棵空樹,或者是具有下列性質的二叉樹:
(1)、若它的左子樹不為空,則左子樹上所有結點的值均小於它的根結點的值;
(2)、若它的右子樹不為空,則右子樹上所有結點的值均大於它的根結點的值;
(3)、它的左、右子樹也分別為二叉查詢樹。
3、二叉查詢樹的基本運算
- /* bst - binary search/sort tree
- * by Richard Tang <[email protected]>
- */
- #include <stdio.h>
- #include <stdlib.h>
- typedefint data_type;
- typedefstruct bst_node {
- data_type data;
- struct bst_node *lchild, *rchild;
- }bst_t, *bst_p;
(1)、插入
在二叉查詢樹中插入新結點,要保證插入新結點後仍能滿足二叉查詢樹的性質。例子中的插入過程如下:
a、若二叉查詢樹root為空,則使新結點為根;
b、若二叉查詢樹root不為空,則通過search_bst_for_insert函式尋找插入點並返回它的地址(若新結點中的關鍵字已經存在,則返回空指標);
c、若新結點的關鍵字小於插入點的關鍵字,則將新結點插入到插入點的左子樹中,大於則插入到插入點的右子樹中。
- static bst_p search_bst_for_insert(bst_p *root, data_type key)
- {
- bst_p s, p = *root;
- while (p) {
- s = p;
- if (p->data == key)
- return NULL;
- p = (key < p->data) ? p->lchild : p->rchild;
- }
- return s;
- }
- void insert_bst_node(bst_p *root, data_type data)
- {
- bst_p s, p;
- s = malloc(sizeof(struct bst_node));
- if (!s)
- perror("Allocate dynamic memory");
- s -> data = data;
- s -> lchild = s -> rchild = NULL;
- if (*root == NULL)
- *root = s;
- else {
- p = search_bst_for_insert(root, data);
- if (p == NULL) {
- fprintf(stderr, "The %d already exists.\n", data);
- free(s);
- return;
- }
- if (data < p->data)
- p->lchild = s;
- else
- p->rchild = s;
- }
- }
(2)、遍歷
- staticint print(data_type data)
- {
- printf("%d ", data);
- return 1;
- }
- int pre_order_traverse(bst_p root, int (*visit)(data_type data))
- {
- if (root) {
- if (visit(root->data))
- if (pre_order_traverse(root->lchild, visit))
- if (pre_order_traverse(root->rchild, visit))
- return 1;
- return 0;
- }
- else
- return 1;
- }
- int post_order_traverse(bst_p root, int (*visit)(data_type data))
- {
- if (root) {
- if (post_order_traverse(root->lchild, visit))
- if (visit(root->data))
- if (post_order_traverse(root->rchild, visit))
- return 1;
- return 0;
- }
- else
- return 1;
- }
中序遍歷二叉查詢樹可得到一個關鍵字的有序序列。
(3)、刪除
刪除某個結點後依然要保持二叉查詢樹的特性。例子中的刪除過程如下:
a、若刪除點是葉子結點,則設定其雙親結點的指標為空。
b、若刪除點只有左子樹,或只有右子樹,則設定其雙親結點的指標指向左子樹或右子樹。
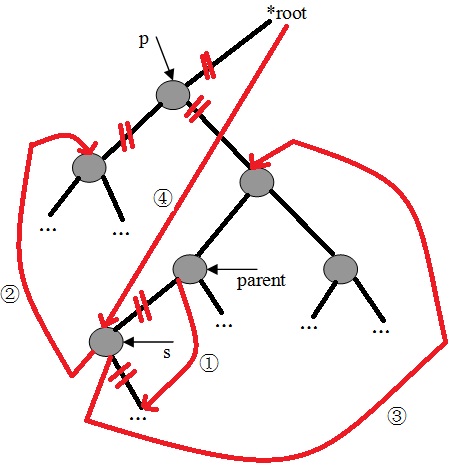
c、若刪除點的左右子樹均不為空,則:
1)、查詢刪除點的右子樹的左子樹是否為空,若為空,則把刪除點的左子樹設為刪除點的右子樹的左子樹。
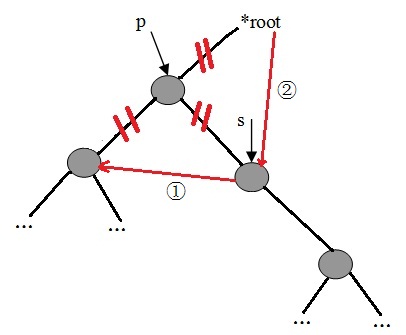
2)、若不為空,則繼續查詢左子樹,直到找到最底層的左子樹為止。
- void delete_bst_node(bst_p *root, data_type data)
- {
- bst_p p = *root, parent, s;
- if (!p) {
- fprintf(stderr, "Not found %d.\n", data);
- return;
- }
- if (p->data == data) {
- /* It's a leaf node */
- if (!p->rchild && !p->lchild) {
- *root = NULL;
- free(p);
- }
- /* the right child is NULL */
- elseif (!p->rchild) {
- *root = p->lchild;
- free(p);
- }
- /* the left child is NULL */
- elseif (!p->lchild) {
- *root = p->rchild;
- free(p);
- }
- /* the node has both children */
- else {
- s = p->rchild;
- /* the s without left child */
- if (!s->lchild)
- s->lchild = p->lchild;
- /* the s have left child */
- else {
- /* find the smallest node in the left subtree of s */
- while (s->lchild) {
- /* record the parent node of s */
- parent = s;
- s = s->lchild;
- }
- parent->lchild = s->rchild;
- s->lchild = p->lchild;
- s->rchild = p->rchild;
- }
- *root = s;
- free(p);
- }
- }
- elseif (data > p->data) {
- delete_bst_node(&(p->rchild), data);
- }
- elseif (data < p->data) {
- delete_bst_node(&(p->lchild), data);
- }
- }
4、二叉查詢樹的查詢分析
同樣的關鍵字,以不同的插入順序,會產生不同形態的二叉查詢樹。
- int main(int argc, char *argv[])
- {
- int i, num;
- bst_p root = NULL;
- if (argc < 2) {
- fprintf(stderr, "Usage: %s num\n", argv[0]);
- exit(-1);
- }
- num = atoi(argv[1]);
- data_type arr[num];
- printf("Please enter %d integers:\n", num);
- for (i = 0; i < num; i++) {
- scanf("%d", &arr[i]);
- insert_bst_node(&root, arr[i]);
- }
- printf("\npre order traverse: ");
- pre_order_traverse(root, print);
- printf("\npost order traverse: ");
- post_order_traverse(root, print);
- printf("\n");
- delete_bst_node(&root, 45);
-
相關推薦
詳解二叉查詢樹演算法的實現(c語言)
樹(Tree)是n(n≥0)個結點的有限集。在任意一棵非空樹中:(1)有且僅有一個特定的被稱為根(Root)的結點;(2)當n>1時,其餘結點可分為m(m>0)個互不相交的有限集T1,T2,…,Tm,其中每一個集合本身又是一棵樹,並且稱為根的子樹(SubTre
二叉查詢樹的實現(插入+遞迴呼叫)
package BinaryTree; public class BinarySearchTree { public TreeNode root; public BinarySearchTree(){ //root=new TreeNode(1,"A");
資料結構---二叉搜尋樹BST實現(C++)
1. 二叉查詢樹 二叉查詢樹(Binary Search Tree),也稱為二叉搜尋樹、有序二叉樹(ordered binary tree)或排序二叉樹(sorted binary tree),是指一棵空樹或者具有下列性質的二叉樹: 若任意節點的左子樹不空,則左子樹上所有節點的值均小於它的根節點的值
線索二叉樹的實現(C語言)
概念 鑑於普通二叉樹使用過程中會出現空間的浪費,後人對在在二叉樹的的基礎上做了改進,利用它的空指標域存放在某種遍歷次序下指向它的前驅結點,和後繼結點的指標。這些指標稱為線索,相應的二叉樹就成了線索二叉樹。 結點結構 Ltag為0時指向該結點的左孩子,
演算法4-6:KMP字串模式匹配演算法實現 (c語言)
[提交] [統計] [提問] 題目描述 KMP演算法是字串模式匹配演算法中較為高效的演算法之一,其在某次子串匹配母串失敗時並未回溯母串的指標而是將子串的指標移動到相應的位置。嚴蔚敏老師的書中詳細描述了KMP演算法,同時前面的例子中也描述了子串移動位置的陣列實現的演算法。前面你已經實現
資料結構—樹的實現(C語言)
1、樹的概念 樹形結構是節點之間以及分支關係定義的層次結構。作為一種重要的非線性結構,樹形結構中一個節點最多隻有一個前驅節點,但是可以有多個後繼節點。2、樹的儲存結構 在計算機中,樹有多種的儲存方式,下面介紹一種動態的“左子/右兄”二叉連結串列表示方法。#incl
【作業系統】銀行家演算法實現(C語言)
# 【作業系統】銀行家演算法實現(C語言) ##### 注意:本人編碼水平很菜。算是自己的一個總結。可能會有我還沒有發現的bug。如果有人發現後可以指出,不勝感激。 ## 1.銀行家演算法: > 我們可以把作業系統看作是銀行家,作業系統管理的資源相當於銀行家管理的資金,程序向作業系統請求分配資源相當於
資料結構之二叉查詢樹Java實現原始碼及註釋
二叉查詢樹(Binary Search Tree),(又:二叉搜尋樹,二叉排序樹)它或者是一棵空樹,或者是具有下列性質的二叉樹: 若它的左子樹不空,則左子樹上所有結點的值均小於它的根結點的值; 若它的右子樹不空,則右子樹上所有結點的值均大於它的根結點的值; 它的左、右子樹也分別為二叉排序樹。以下是樓主用jav
B族樹詳解(二叉搜尋樹、B-樹、B+樹、B*樹)
二叉搜尋樹 二叉搜尋樹: 1.所有非葉子結點至多擁有兩個兒子(Left和Right); 2.所有結點儲存一個關鍵字; 3.非葉子結點的左指標指向小於其關鍵字的子樹,右指標指向大於其關鍵字的子樹; 如: B樹的搜尋,
二叉查詢樹的查詢、插入、刪除、釋放等基本操作的實現(C語言)
二叉查詢樹是一種特殊性質的二叉樹,該樹中的任何一個節點,它的左子樹(若存在)的元素值小於節點的元素值,右子樹(若存在)的元素值大於節點的元素值。 實現了二叉樹查詢樹的實現以及基本操作,包括查詢、插入、刪除、初始化、釋放等。 原始碼下載地址:http://download.c
二叉搜尋樹Java實現(查詢、插入、刪除、遍歷)
1 class Node { 2 int key; 3 int value; 4 Node leftChild; 5 Node rightChild; 6 7 public Node(int key, int value) { 8
AVL樹-自平衡二叉查詢樹(Java實現)
在電腦科學中,AVL樹是最先發明的自平衡二叉查詢樹。AVL樹得名於它的發明者 G.M. Adelson-Velsky 和 E.M. Landis,他們在 1962 年的論文 "An algorithm for the organization of inform
詳解二叉排序樹
二叉排序樹的插入、查詢、刪除 二叉排序樹的定義 二叉排序樹右稱二叉查詢樹。或者為空樹,或者是具有以下性質: (1)若它的左子樹不為空,則左子樹所有節點的值小於根結點, (2)若它的右子樹不為空,則根結點的值小於所有右子樹結點的值 (3)它的左右子樹葉分別為二叉排序樹 總結
二叉樹-詳解二叉排序樹
二叉搜尋樹 首先二叉排序樹也是一棵二叉樹,所謂二叉樹,就是“任何節點最多隻允許兩個子節點”,這兩個子節點稱為左右子節點。如下便是一個二叉樹。 1、二叉排序樹性質: 1、就是若它的左子樹不空,則左子樹上所有節點的值均小於它的根節點的值; 2、若它的右子樹不空
二叉搜尋樹的查詢、插入、刪除的遞迴與非遞迴實現(C語言)
【概念】 什麼是二叉搜尋樹? 二叉搜尋樹又稱二叉排序樹(按照中序遍歷,可以得到一組有序的序列),它或者是一顆空樹,或者是具有以下性質的二叉樹: 若他的左子樹不為空,則左子樹上所有節點的值都小於根結點的值。 若他的
二叉查詢樹python實現
1. 二叉查詢樹的定義: 左子樹不為空的時候,左子樹的結點值小於根節點,右子樹不為空時,右子樹的結點值大於根節點,左右子樹分別為二叉查詢樹 2. 二叉查詢樹的最左邊的結點即為最小值,要查詢最小值,只需遍歷左子樹的結點直到為空為止,同理,最右邊的結點結尾最大值,要查詢最大值,
二叉查詢樹的平衡(DSW演算法)
樹適合於表示某些領域的層次結構(比如Linux的檔案目錄結構),使用樹進行查詢比使用連結串列快的多,理想情況下樹的查詢複雜度O(log(N)),而連結串列為O(N),但理想情況指的是什麼情況呢?一般指樹是完全平衡的時候。哪最壞的情況是什麼呢?就是樹退化為連結串列的時,這時候查詢的複雜度與連結串列相同。就失去了
Python資料結構——二叉搜尋樹的實現(下)
搜尋樹實現(續) 最後,我們把注意力轉向二叉搜尋樹中最具挑戰性的方法,刪除一個鍵值(參見Listing 7)。首要任務是要找到搜尋樹中要刪除的節點。如果樹有一個以上的節點,我們使用_get方法找到需要刪除的節點。如果樹只有一個節點,這意味著我們要刪除樹的根,但是我們仍然要檢查根的鍵值是否與要刪除的鍵值匹配。
二叉樹插入和刪除操作的遞迴實現(c語言)
連結串列和陣列是最常見的資料結構,對於資料結構來說,查詢(Find),最大最小值(FindMin,FindMax),插入(Insert)和刪除(Delete)操作是最基本的操作。對於連結串列和陣列來說,這些操作的時間界為O(N),其中N為元素的個數。陣列的插入和刪除需要對其他
Python資料結構——二叉搜尋樹的實現(上)
二叉搜尋樹 我們已經知道了在一個集合中獲取鍵值對的兩種不同的方法。回憶一下這些集合是如何實現ADT(抽象資料型別)MAP的。我們討論兩種ADT MAP的實現方式,基於列表的二分查詢和雜湊表。在這一節中,我們將要學習二叉搜尋樹,這是另一種鍵指向值的Map集合,在這種情況下我們不用
