B樹是為實現高效的磁碟存取而設計的多叉平衡搜尋樹。這個概念在檔案系統，資料庫系統中非常重要。當然，有關於B樹的產生，發展，結構等等方面的介紹已經非常詳細，所以本文只是介紹有關於B樹和B+樹最核心的知識點，也算是我本人的學習筆記。至於詳細的資料，因為畢竟有著太多，所以不再贅述。可以向大家推薦一篇部落格：從B樹、B+樹、B*樹談到R 樹，這篇文章中，作者對於B樹系列資料結構的講解非常詳細，我的這篇部落格，也是大量參考了人家的很多例子和描述。

B樹

一、基本原理

首先，簡單說一下B樹產生的原因。B樹是一種查詢樹，我們知道，這一類樹（比如二叉查詢樹，紅黑樹等等）最初生成的目的都是為了解決某種系統中，查詢效率低的問題。B樹也是如此，它最初啟發於二叉查詢樹，二叉查詢樹的特點是每個非葉節點都只有兩個孩子節點。然而這種做法會導致當資料量非常大時，二叉查詢樹的深度過深，搜尋演算法自根節點向下搜尋時，需要訪問的節點也就變的相當多。如果這些節點儲存在外儲存器中，每訪問一個節點，相當於就是進行了一次I/O操作，隨著樹高度的增加，頻繁的I/O操作一定會降低查詢的效率。

這裡有一個基本的概念，就是說我們從外儲存器中讀取資訊的步驟，簡單來分，大致有兩步：

1. 找到儲存這個資料所對應的磁碟頁面，這個過程是機械化的過程，需要依靠磁臂的轉動，找到對應磁軌，所以耗時長。
2. 讀取資料進記憶體，並實施運算，這是電子化的過程，相當快。

綜上，對於外儲存器的資訊讀取最大的時間消耗在於尋找磁碟頁面。那麼一個基本的想法就是能不能減少這種讀取的次數，在一個磁碟頁面上，多儲存一些索引資訊。B樹的基本邏輯就是這個思路，它要改二叉為多叉，每個節點儲存更多的指標資訊，以降低I/O運算元。

二、基本結構

1. B樹的定義

有關於B樹概念的定義，不同的資料在表述上有所差別。我在這裡採用《算導》中的定義，用最小度t t 來定義B樹。一棵最小度為t t 的B樹是滿足如下四個條件的平衡多叉樹：

• 每個節點最多包含2t−1 2t−1 個關鍵字；除根節點外的每個節點至少有t−1 t−1 個關鍵字（t≤2 t≤2 ），根節點至少有一個關鍵字；

• 一個節點u u 中的關鍵字按非降序排列：u.key 1 ≤u.key 2 ≤…u.key n  u.key1≤u.key2≤…u.keyn ；

• 每個節點的關鍵字對其子樹的範圍分割。設節點u u 有n+1 n+1 個指標，指向其n+1 n+1 棵子樹，指標為u.p 1 ,…u.p n  u.p1,…u.pn ，關鍵字k i  ki 為u.p i  u.pi 所指的子樹中的關鍵字，有k 1 ≤u.key 1 ≤k 2 ≤u.key 2 … k1≤u.key1≤k2≤u.key2… 成立；

• 所有葉子節點具有相同的深度，即樹的高度h h 。這表明B樹是平衡的。平衡性其實正是B樹名字的來源，B表示的正是單詞Balanced；

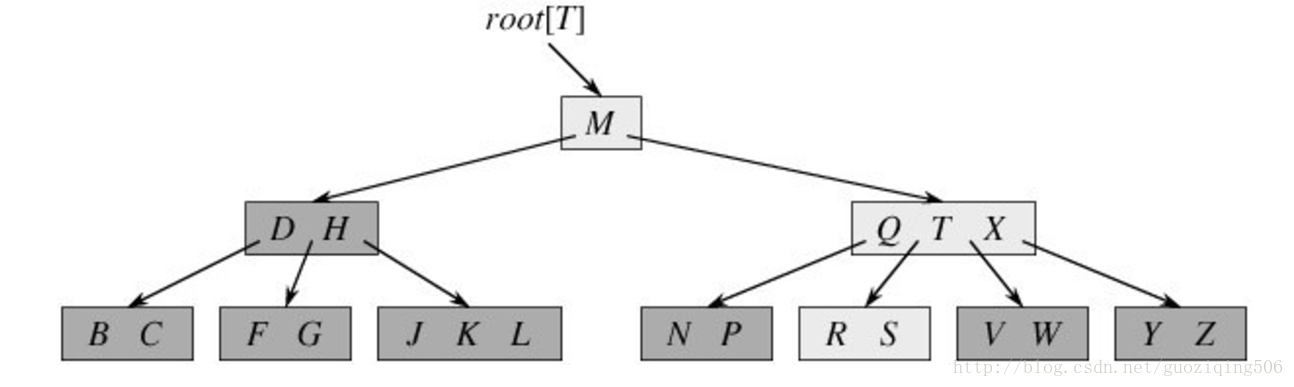
一個標準的B樹如下圖：

2. B樹的高度

我直接給出結論了：對於一個包含n n 個關鍵字(n≥1 n≥1 )，最小度數t≥2 t≥2 的B樹T，其高度h h 滿足如下規律：

h≤log t n+12  h≤logt⁡n+12

在搜尋B樹時，很明顯，訪問節點（即讀取磁碟）的次數與樹的高度呈正比，而B樹與紅黑樹和普通的二叉查詢樹相比，雖然高度都是對數數量級，但是顯然B樹中log log 函式的底可以比2更大，因此，和二叉樹相比，極大地減少了磁碟讀取的次數。

三、搜尋演算法

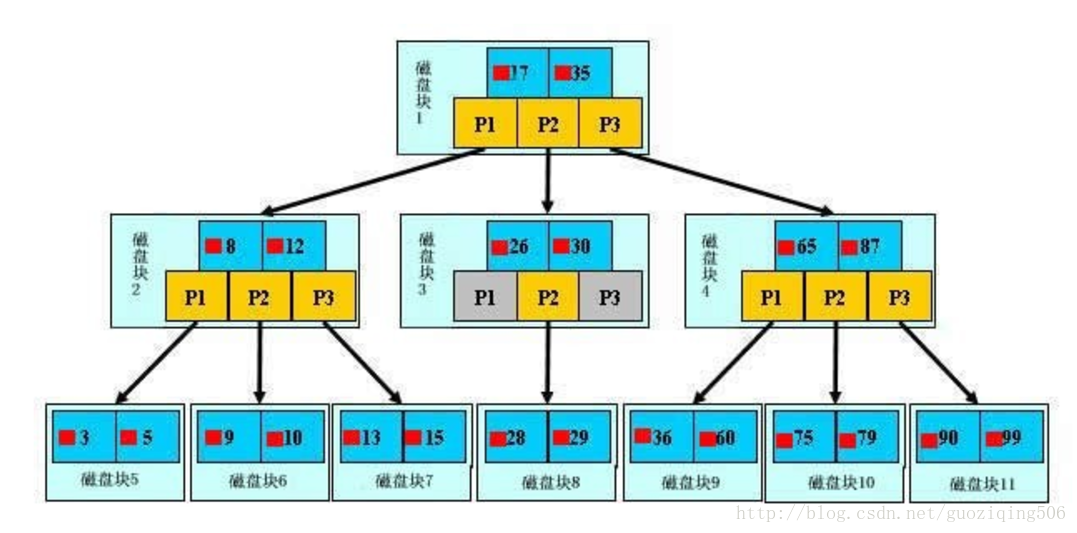
這裡，我直接用部落格從B樹、B+樹、B*樹談到R 樹中的例子（因為這個例子非常好，也有現成的圖示，就直接拿來用，不再自己班門弄斧了），一棵已經建立好的B樹如下圖所示，我們的目的是查詢關鍵字為29的檔案：

先簡單對上圖說明一下：

• 圖中的小紅方塊表示對應關鍵字所代表的檔案的儲存位置，實際上可以看做是一個地址，比如根節點中17旁邊的小紅塊表示的就是關鍵字17所對應的檔案在硬碟中的儲存地址。

• P是指標，不用多說了，需要注意的是：指標，關鍵字，以及關鍵字所代表的檔案地址這三樣東西合起來構成了B樹的一個節點，這個節點儲存在一個磁碟塊上

下面，看看搜尋關鍵字的29的檔案的過程：

1. 從根節點開始，讀取根節點資訊，根節點有2個關鍵字：17和35。因為17 < 29 < 35，所以找到指標P2指向的子樹，也就是磁碟塊3（1次I/0操作）

2. 讀取當前節點資訊，當前節點有2個關鍵字：26和30。26 < 29 < 30，找到指標P2指向的子樹，也就是磁碟塊8（2次I/0操作）

3. 讀取當前節點資訊，當前節點有2個關鍵字：28和29。找到了！（3次I/0操作）

由上面的過程可見，同樣的操作，如果使用平衡二叉樹，那麼需要至少4次I/O操作，B樹比之二叉樹的這種優勢，還會隨著節點數的增加而增加。另外，因為B樹節點中的關鍵字都是排序好的，所以，在節點中的資訊被讀入記憶體之後，可以採用二分查詢這種快速的查詢方式，更進一步減少了讀入記憶體之後的計算時間，由此更能說明對於外存資料結構來說，I/O次數是其查詢資訊中最大的時間消耗，而我們要做的所有努力就是儘量在搜尋過程中減少I/O操作的次數。

四、向B樹插入關鍵字

向B樹種插入關鍵字的過程與向二叉查詢樹中插入關鍵字的過程類似，但是要稍微複雜一點，因為根據上面B樹的定義，我們可以看出，B樹每個節點中關鍵字的個數是有範圍要求的，同時，B樹是平衡的，所以，如果像二叉查詢樹那樣，直接找到相關的葉子，插入關鍵字，有可能會導致B樹的結構發生變化而這種變化會使得B樹不再是B樹。

所以，我們這樣來設計B樹種對新關鍵字的插入：首先找到要插入的關鍵字應該插入的葉子節點（為方便描述，設這個葉子節點為u u ），如果u u 是滿的（恰好有2t−1 2t−1 個關鍵字），那麼由於不能將一個關鍵字插入滿的節點，我們需要對u u 按其當前排在中間關鍵字u.key t  u.keyt 進行分裂，分裂成兩個節點u 1 ,u 2  u1,u2 ；同時，作為分裂標準的關鍵字u.key t  u.keyt 會被上移到u u 的父節點中，在u.key t  u.keyt 插入前，如果u u 的父節點未滿，則直接插入即可；如果u u 的父節點已滿，則按照上面的方法對u u 的父節點分裂，這個過程如果一直不停止的話，最終會導致B樹的根節點分裂，B樹的高度增加一層。

我用《算導》中的一個題目展示一下這種插入關鍵字的過程：

現在我們要將關鍵字序列：F, S, Q, K, C, L, H, T, V, W, M, R, N, P, A, B, X, Y依次插入一棵最小度為2的B樹中。也就是說，這棵樹的節點中，最多有3個關鍵字，最少有1個關鍵字。

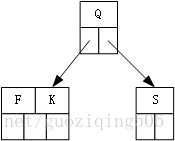
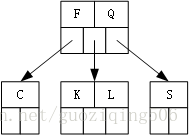
第1步，F, S, Q可以被插入一個節點（也就是根節點）

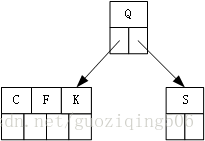
第2步，插入關鍵字K，因為節點已滿，所以在插入前，發生分裂，中間關鍵字Q上移，建立了一個新的根節點：

第3步，插入關鍵字C:

第4步，插入關鍵字L，L應該被插入到根節點的左側的孩子中，因為此時該節點已滿，所以在插入前，發生分裂：

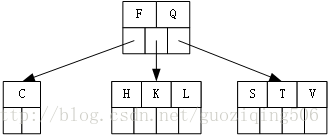
第5步，插入關鍵字H, T, V，這個過程沒有發生節點的分裂：

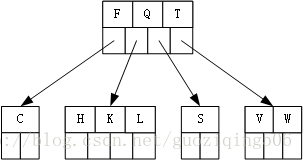
第6步，插入關鍵字W，W應該被插入到根節點的最右側的孩子中，因為此時該節點已滿，所以在插入前，關鍵字T上移，最右端的葉子節點發生分裂：

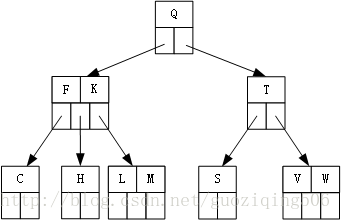
第7步，插入關鍵字M，M應該被插入到根節點的左起第2個孩子中，因為此時該節點已滿，所以在插入前，發生分裂，分裂之後，中間關鍵字K上移，導致根節點發生分裂，樹高增加1：

第8步，同樣的道理，插入關鍵字R, N, P, A, B, X, Y：最終得到的B樹如下：

五、從B樹刪除關鍵字

刪除操作的基本思想和插入操作是一樣的，都是不能因為關鍵字的改變而改變B樹的結構。插入操作主要防止的是某個節點中關鍵字的個數太多，所以採用了分裂；刪除則是要防止某個節點中，因刪除了關鍵字而導致這個節點的關鍵字個數太少，所以採用了合併操作。

下面分三種情況來討論下刪除操作是如何工作的，這個過程的順序是自根節點起向下遍歷B樹

Case - 1：如果要刪除的關鍵字k k 在節點u u 中，而且u u 是葉子節點，那麼直接刪除k k

Case - 2：如果要刪除的關鍵字k k 在節點u u 中，而且u u 是內部節點，那麼分以下3種情況討論：

(1) 如果u u 中前於k k 的子節點u 1  u1 中至少含有t t 個關鍵字，則找出k k 在以u 1  u1 為根的子樹中的前驅k ′  k′ （前驅的意思是u 1  u1 中比k k 小的關鍵字中最大的），然後在以u 1  u1 為根的子樹中刪除k ′  k′ ，並在u u 中以k ′  k′ 替代k k

(2) 如果上面的條件(1)不成立，也就是說，前於k k 的子節點中關鍵字的個數小於t t 了，那麼就去找後於k k 的子節點，記為u 2  u2 。若u 2  u2 中至少含有t t 個關鍵字，則找出k k 在以u 2  u2 為根的子樹中的後繼k ′  k′ (大於k k 的關鍵字中最小的)，然後在以u 2  u2 為根的子樹中刪除k ′  k′ ，並在u u 中以k ′  k′ 替代k k 。可以看出（2）是（1）的一個對稱過程

(3) 如果u 1 ,u 2  u1,u2 中的關鍵字個數都是t−1 t−1 ，則將k k 和u 2  u2 合併後併入u 1  u1 ，這樣u u 就失去了k k 和指向u 2  u2 的指標，最後遞迴地從u 1  u1 中刪除k k

Case - 3：如果要刪除的關鍵字k k 不在當前節點u u 中，而且u u 是內部節點（如果自上而下掃描到葉子都沒有這個關鍵字的話，那就說明要刪除的關鍵字根本就不存在，所以此處只考慮u u 是內部節點的情況），則首先確定包含k k 的u u 的子樹，我們這裡設為u.p i  u.pi 。如果u.p i  u.pi 中至少含有t t 個關鍵字，那麼繼續掃描，尋找下一個要被掃描的子樹；如果u.p i  u.pi 中只含有t−1 t−1 個關鍵字，則需要分下面兩種情況進行操作：

(1) 如果u.p i  u.pi 至少有一個相鄰的兄弟比較“豐滿”（即這個兄弟至少有t t 個關鍵字）。則將u u 中的一個關鍵字降至u.p i  u.pi ，同時令u.p i  u.pi 的最“豐滿”的兄弟中升一個關鍵至u u 。然後繼續掃描B樹，尋找k k

(2) 如果u.p i  u.pi 的兩個相鄰的兄弟都不“豐滿”（都只有t−1 t−1 個關鍵字）。則令u.p i  u.pi 和其一個兄弟合併，再將u u 的一個關鍵字降至新合併的節點。使之成為該節點的中間關鍵字。

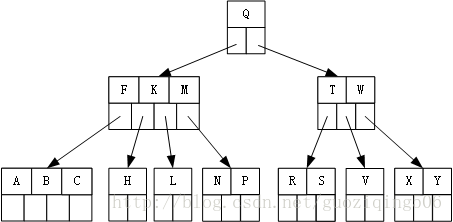
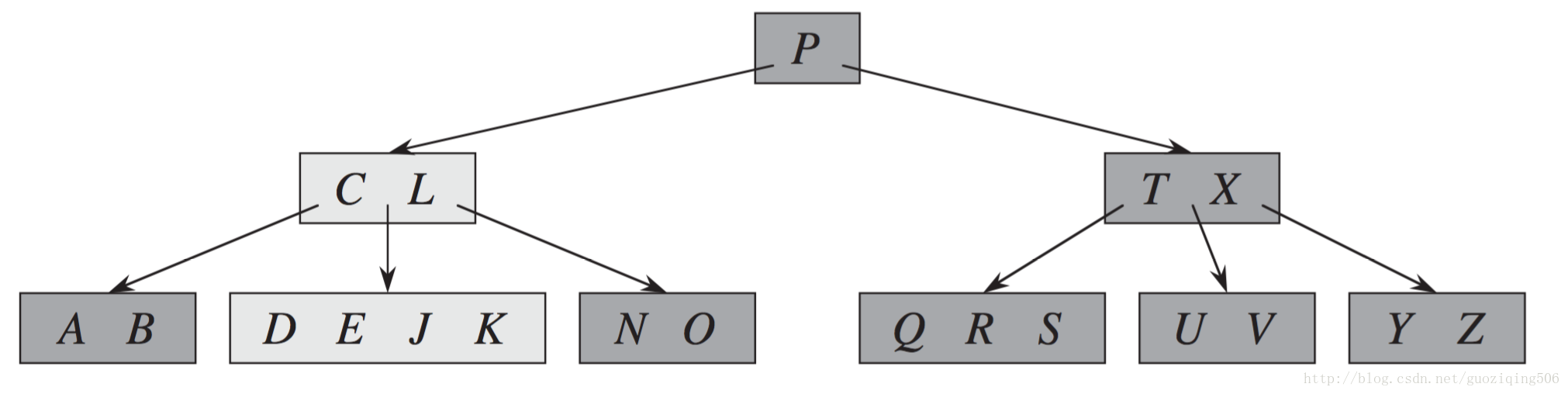
舉個例子，就可以清晰看到上面說的這幾種刪除的情況。拿下圖所示的最小度為3的B樹為例（即樹中除根和葉子之外的節點只能有2，3，4三種情況的關鍵字個數）：

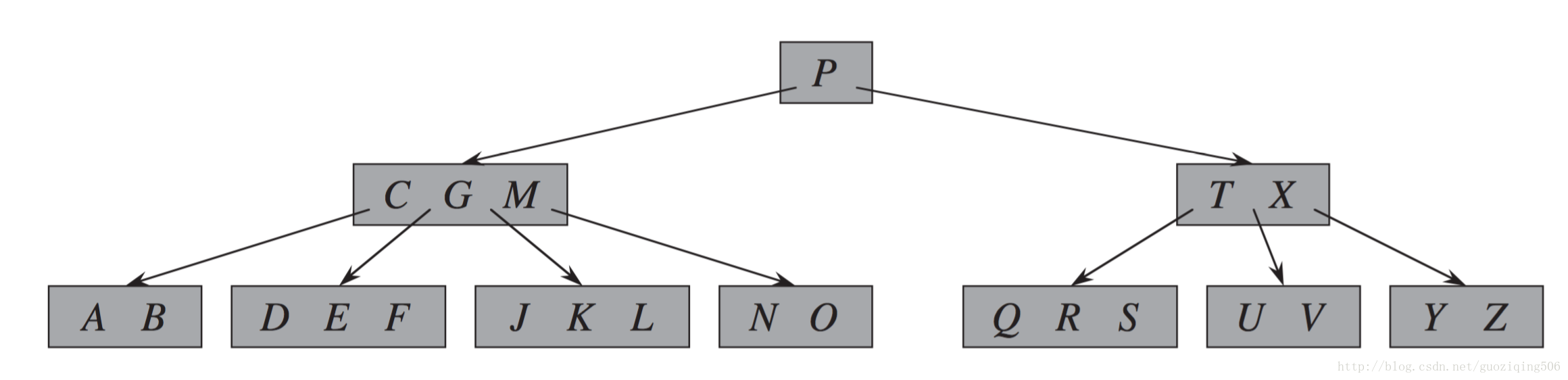
Step 1: 刪除上圖中的關鍵字F，過程如下：先掃描根節點（含P），再掃描其左孩子（含CGM），發現豐滿，繼續掃描到左起第二個葉子，然後就是符合Case - 1的情況了。結果如下圖所示：

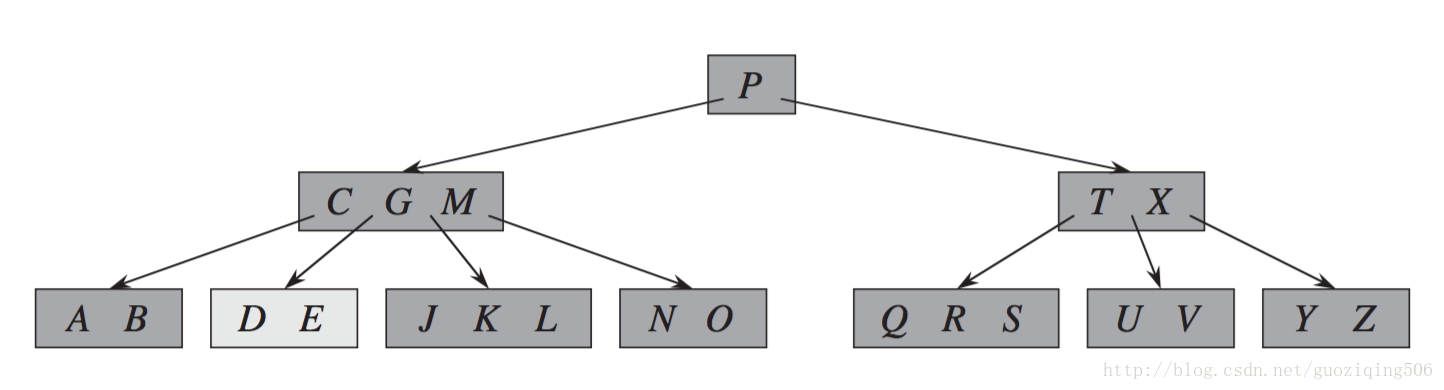
Step 2: 再刪除M，此時遇到Case - 2(1)的情況，結果如下圖所示：

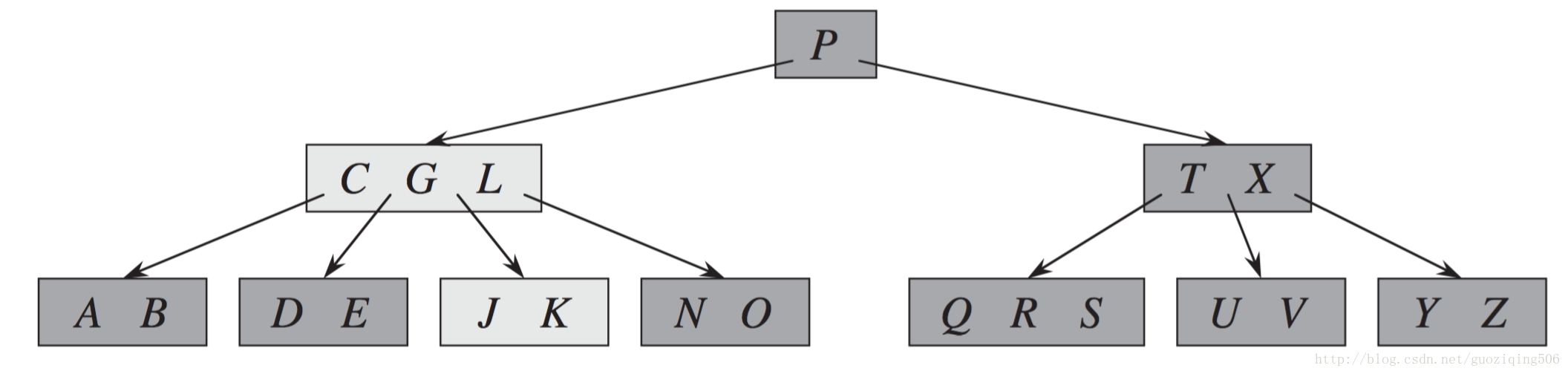
Step 3: 再刪除G，G的前驅、後驅都是不豐滿的。也就是Case - 2(3)的情況，結果如下圖所示：

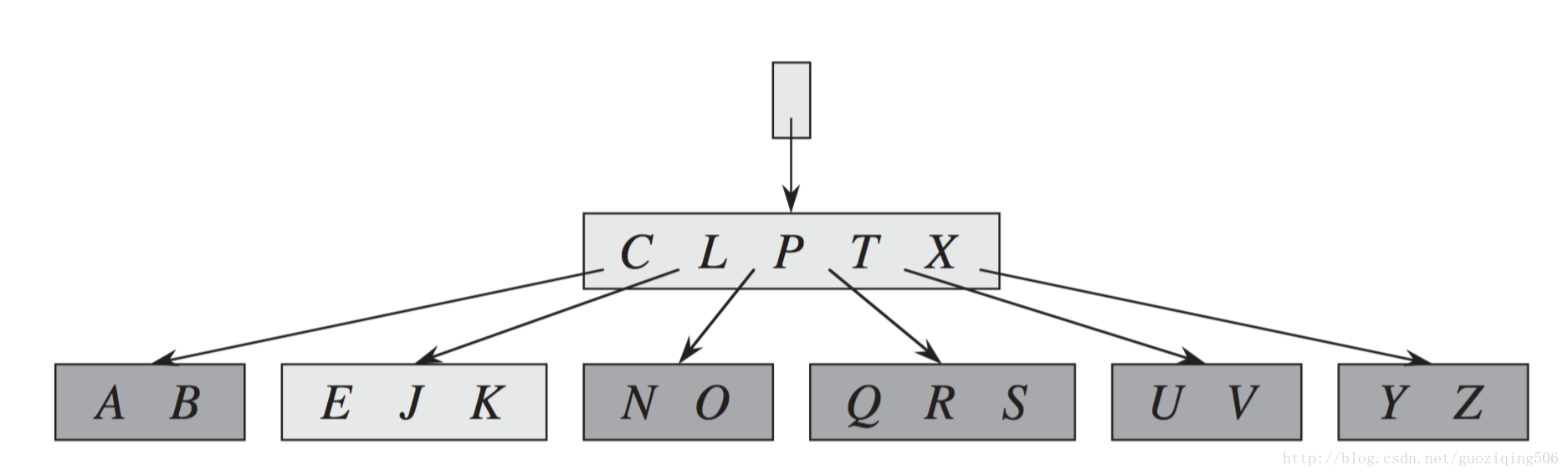
Step 4: 再刪除D，掃描至含CL的節點後，發現它不豐滿，且他的兄弟也不豐滿。則將節點CL和TX合併，並降關鍵字P至新合併的節點。也就是Case - 3(2)的情況，結果如下圖所示，此時，樹高減1：

Step 5: 再刪除B，也就是Case - 3(1)的情況，結果如下圖所示：

下面總結一下B樹的刪除原理：

1. 基本原則是不能破壞關鍵字個數的限制；
2. 如果在當前節點中，找到了要刪的關鍵字，且當前節點為內部節點。那麼，如果有比較豐滿的前驅或後繼，借一個上來，再把要刪的關鍵字降下去，在子樹中遞迴刪除；如果沒有比較豐滿的前驅或後繼，則令前驅與後繼合併，把要刪的關鍵字降下去，遞迴刪除；
3. 如果在當前節點中，還未找到要刪的關鍵字，且當前節點為內部節點。那麼去找下一步應該掃描的孩子，並判斷這個孩子是否豐滿，如果豐滿，繼續掃描；如果不豐滿，則看其有無豐滿的兄弟，有的話，從父親那裡接一個，父親再找其最豐滿的兄弟借一個；如果沒有豐滿的兄弟，則合併，再令父親下降，以保證B樹的結構。

B+樹

B+樹的定義

B+樹是B樹的一種變形，它更適合實際應用中作業系統的檔案索引和資料庫索引。定義如下：（為和大多資料保持一致，這裡使用階數m m 來定義B+樹，而不像之前的B樹中，使用的是最小度t t 來定義）

1. 除根節點外的內部節點，每個節點最多有m m 個關鍵字，最少有⌈m2 ⌉ ⌈m2⌉ 個關鍵字。其中每個關鍵字對應一個子樹（也就是最多有m m 棵子樹，最少有⌈m2 ⌉ ⌈m2⌉ 棵子樹）；
2. 根節點要麼沒有子樹，要麼至少有2棵子樹；

3. 所有的葉子節點包含了全部的關鍵字以及這些關鍵字指向檔案的指標，並且：

   • 所有葉子節點中的關鍵字按大小順序排列
   • 相鄰的葉子節點順序連結（相當於是構成了一個順序連結串列）
   • 所有葉子節點在同一層
4. 所有分支節點的關鍵字都是對應子樹中關鍵字的最大值

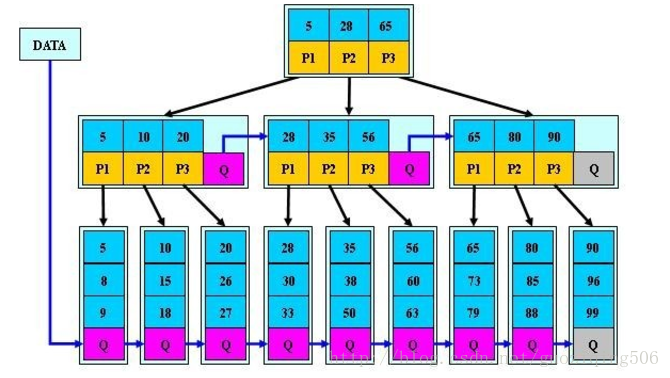
比如，下圖就是一個非常典型的B+樹的例子。

B+樹和B樹相比，主要的不同點在以下3項：

• 內部節點中，關鍵字的個數與其子樹的個數相同，不像B樹種，子樹的個數總比關鍵字個數多1個
• 所有指向檔案的關鍵字及其指標都在葉子節點中，不像B樹，有的指向檔案的關鍵字是在內部節點中。換句話說，B+樹中，內部節點僅僅起到索引的作用，
• 在搜尋過程中，如果查詢和內部節點的關鍵字一致，那麼搜尋過程不停止，而是繼續向下搜尋這個分支。

根據B+樹的結構，我們可以發現B+樹相比於B樹，在檔案系統，資料庫系統當中，更有優勢，原因如下：

1. B+樹的磁碟讀寫代價更低
   B+樹的內部結點並沒有指向關鍵字具體資訊的指標。因此其內部結點相對B樹更小。如果把所有同一內部結點的關鍵字存放在同一盤塊中，那麼盤塊所能容納的關鍵字數量也越多。一次性讀入記憶體中的需要查詢的關鍵字也就越多。相對來說I/O讀寫次數也就降低了。

2. B+樹的查詢效率更加穩定
   由於內部結點並不是最終指向檔案內容的結點，而只是葉子結點中關鍵字的索引。所以任何關鍵字的查詢必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同，導致每一個數據的查詢效率相當。

3. B+樹更有利於對資料庫的掃描
   B樹在提高了磁碟IO效能的同時並沒有解決元素遍歷的效率低下的問題，而B+樹只需要遍歷葉子節點就可以解決對全部關鍵字資訊的掃描，所以對於資料庫中頻繁使用的range query，B+樹有著更高的效能。