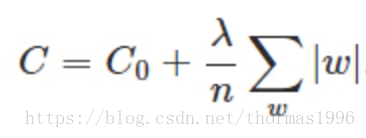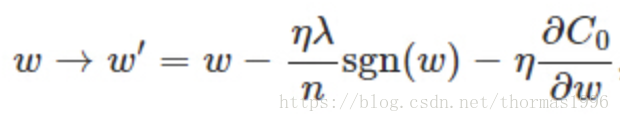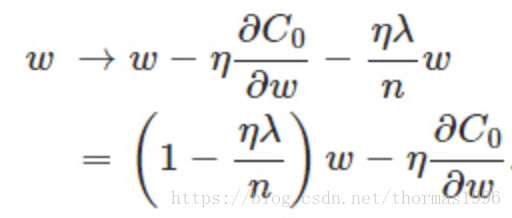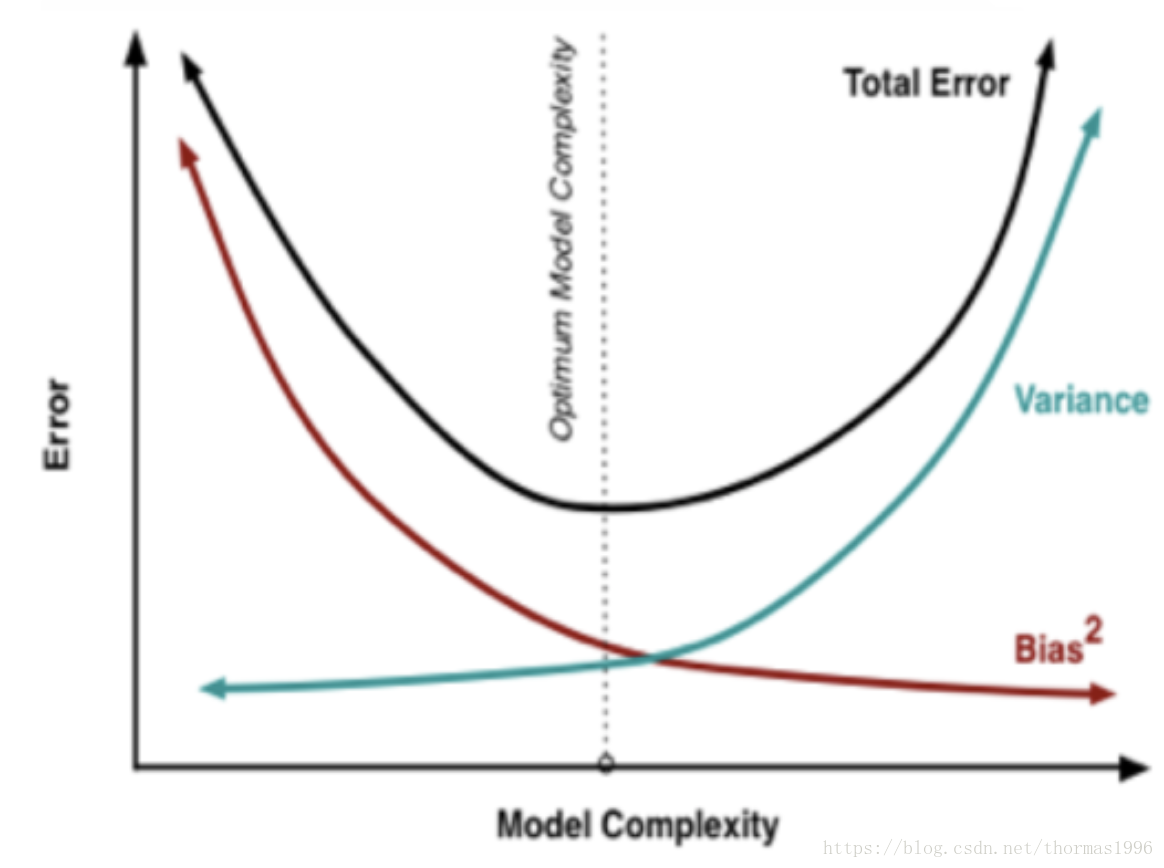
偏差和方差

• 在統計學習框架下，Error = Bias + Variance。Error指的模型的預測錯誤率，由兩部分組成，一部分是由於模型太簡單而帶來的估計不準確的部分（Bias），另一部分是由於模型太複雜而帶來的更大的變化空間和不確定性（Variance）。
• 如果要降低模型的Bias，就一定程度上會提高模型的Variance，反之亦然。根本原因是如果我們更相信訓練資料的真實性，忽視對模型的先驗知識，就會保證模型在訓練樣本上的準確度，這樣可以減少模型的Bias，但這樣會使模型的泛化能力不夠，導致過擬合，降低模型在真實資料上的表現，增加模型的不確定性。反之，如果我們更注重模型的先驗知識，在學習模型的過程中對模型增加更多的限制，就可以降低模型的variance，提高模型的穩定性，但也會使模型的Bias增大。
• 模型太簡單：欠擬合；模型太複雜：過擬合。

抑制欠擬合與過擬合方法

欠擬合主要是因為模型太簡單，不能很好地捕捉模型特徵。

• 新增其他特徵項讓模型學習
• 使模型更復雜，比如說對一個線性模型新增多項式特徵等
• 減少正則化引數

過擬合主要是因為模型太複雜，過度擬合訓練資料，或是訓練資料太少，導致模型不能很好地學習到全域性特徵。

• 清洗資料，去掉outliner
• 擴大資料集，包括從資料來源頭採集更多資料，複製原有資料並加上隨機噪聲，重取樣，根據當前資料集估計資料分佈引數，使用該分佈產生更多資料等方法
• Early stopping，當valid準確率不提高時適時停止
• 正則化，包括L0正則、L1正則和L2正則
• dropout

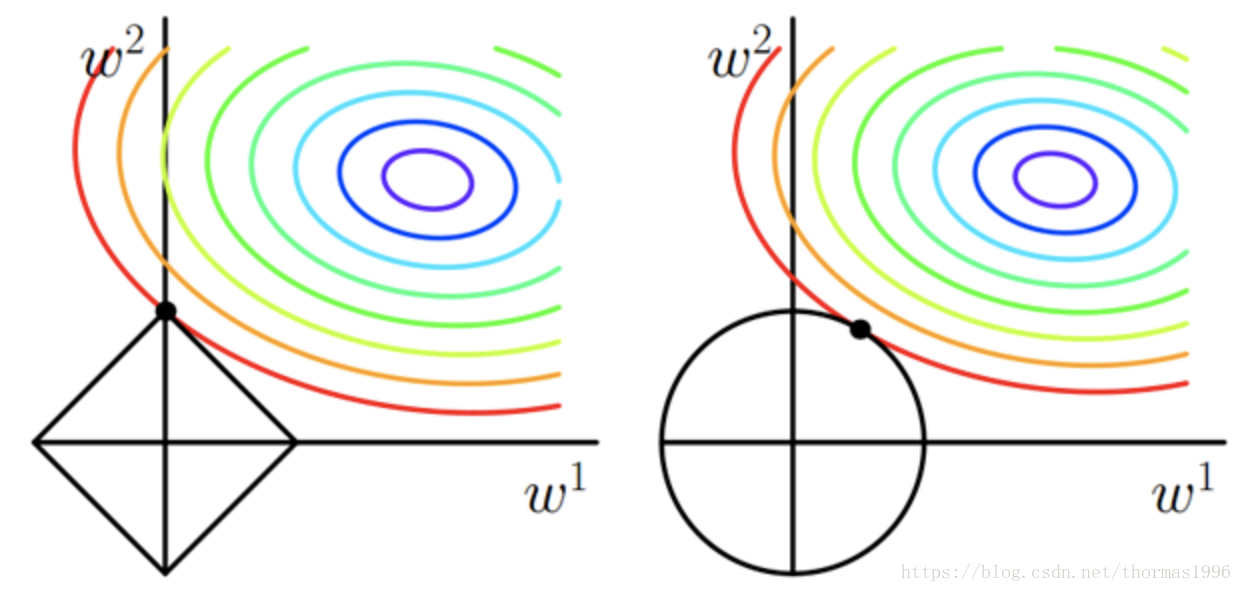
L1與L2正則化說明和區別

L0範數：向量中非0元素的個數。

L1範數(Lasso Regularization)：向量中各個元素絕對值的和。

L2範數(Ridge Regression)：向量中各元素平方和求平方根。

L1正則化也叫Lasso迴歸（圖左）：

可以看到如果ω為正，那麼L1使ω減小，反之ω為負，L1使ω增大，也就是L1會讓ω趨向於零，因此產生稀疏解。網路引數越多為零，可以認為模型越簡單，有助於抑制過擬合。

缺點是在原點無法求導，一般人為定義為原點導數為零。

L2正則化也叫Ridge迴歸（圖右）：

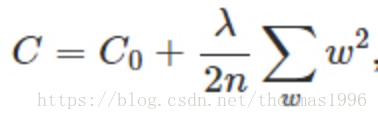
會使ω變小，引數變小一般可以認為使模型更簡單，從而減小過擬合。並且L2正則化可以讓優化求解變得穩定很快速（這是因為加入了L2正規化之後，滿足了強凸）。

為什麼有助於讓優化求解變得穩定很快速的原理可見：https://blog.csdn.net/zouxy09/article/details/24971995

L2對outliner更加敏感，outliner在圖上就是離原點更遠，懲罰就越大，所以L2會讓解更加稠密，向原點靠攏。一般來說，L2在抑制過擬合的表現比L1好。

知乎上對為什麼引數值變小能抑制過擬合有一個更為數學上的解釋：

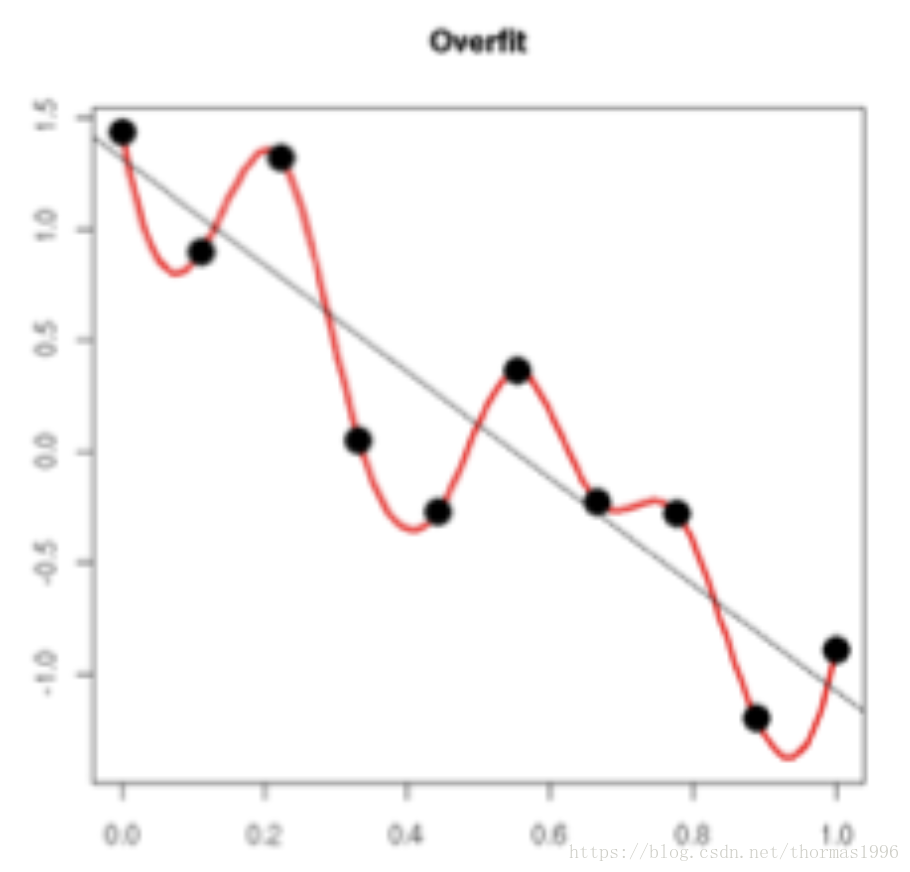
過擬合的時候，擬合函式的係數往往非常大，為什麼？如下圖所示，過擬合，就是擬合函式需要顧忌每一個點，最終形成的擬合函式波動很大。在某些很小的區間裡，函式值的變化很劇烈。這就意味著函式在某些小區間裡的導數值（絕對值）非常大，由於自變數值可大可小，所以只有係數足夠大，才能保證導數值很大。

正則化是通過約束引數的範數使其不要太大，所以可以在一定程度上減少過擬合情況。

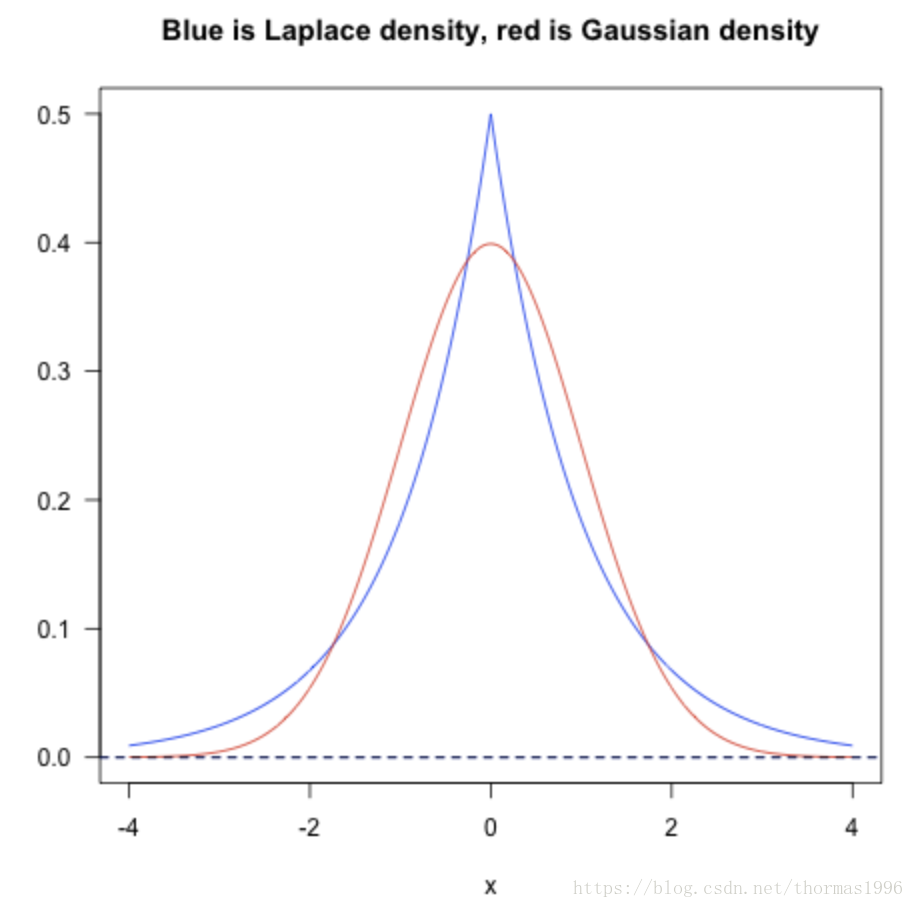
從統計概率的角度來看，L1 Norm和L2 Norm其實對向量中值的分佈有著不同的先驗假設：

藍色是L1，紅色是L2，L1認為是拉普拉斯先驗，L2認為是高斯先驗。可以看出L1對極端情況，也就是outliner忍受度更高。

如何從拉普拉斯和高斯先驗推出L1和L2正則化可見：http://www.cnblogs.com/heguanyou/p/7688344.html

稀疏解的優點

• 能實現特徵的自動選擇，能自動過濾掉很多相關性低的特徵
• 更少的特徵意味著模型更容易解釋

梯度下降演算法

SGD 震盪很厲害

Momentum 改變一階項，考慮之前的batch的影響，能夠在相關方向加速SGD，抑制振盪，從而加快收斂

Ada 學習率自適應的方法，通過二階項的約束，前期加大梯度，後期減小梯度，使得更快收斂。問題是分母的累加可能導致梯度消失太快，提前結束訓練

Adadelta 減少了分母的累加

Rmpop Adadelta的一個變種，善於處理非平穩目標

Adam 結合了Momentum和Ada，結合了Adagrad善於處理稀疏梯度和RMSprop善於處理非平穩目標的優點，效果是最好的

如何避免區域性最小？

• 用多個初始值，選擇誤差最小的引數作為最終結果
• 模擬退火，即在每一步以一定概率接受比當前解更差的結果，該概率隨時間推移而降低，有助於跳出區域性最小
• 隨機梯度下降（SGD），由於每次只選擇部分樣本，有機率跳出區域性最小

為什麼說bagging是減少variance，而boosting是減少bias?

簡單來說如果bagging的n個分類器的樣本都是獨立的，那麼方差可以縮小n倍，偏差不變。儘管一般來說都不是完全獨立的，也能一定程度上減小方差。boosting是用弱分類去訓練錯誤樣本，目標是減少偏差。

詳細解釋可見：https://www.zhihu.com/question/26760839

Batch Normalization歸一化作用

用的不是很多，目的是為了解決不同層之間資料分佈改變導致訓練速度慢等的問題。

可以參考：

https://blog.csdn.net/yujianmin1990/article/details/78764597

https://blog.csdn.net/hjimce/article/details/50866313

特徵選擇

資料屬性過多會造成維度災難，特徵選擇就是從中選出更重要的部分屬性。

• 過濾式：計算相關性，丟掉方差改變小的特徵（方差閾值），丟掉高度相關的特徵（冗餘資訊）。
• 包裹式：利用測試集作為評價標準，反過來選。
• 嵌入式：利用了L1norm直接做篩選。

特徵提取

創造全新的，較小的特徵集

• PCA：選取方差最大化的投影平面
  （1）先對所有樣本中心化，xi = xi - x(average) 
  （2）計算協方差矩陣
  （3）對協方差矩陣用奇異值分解SVD
  （4）選取最大的k個特徵值對應的特徵向量

稀疏表示

稀疏表示本來是最小化L0範數的問題，這往往是一個NP hard的問題，一般用最小化L1範數作為近似。（L1是L0的最優近似）

是對於龐大資料集的一種降維表示，優點是省空間；奧卡姆剃刀說：如果兩個模型的解釋力相同，選擇較簡潔的那個。稀疏表達就符合這一點。

關於模型的選擇

這篇講的很好：https://www.leiphone.com/news/201608/WosBbsYqyfwcDNa4.html

1. 首當其衝應該選擇的就是邏輯迴歸，如果它的效果不怎麼樣，那麼可以將它的結果作為基準來參考，在基礎上與其他演算法進行比較；

2. 然後試試決策樹（隨機森林）看看是否可以大幅度提升你的模型效能。即便最後你並沒有把它當做為最終模型，你也可以使用隨機森林來移除噪聲變數，做特徵選擇；

3. 如果特徵的數量和觀測樣本特別多，那麼當資源和時間充足時（這個前提很重要），使用SVM不失為一種選擇。

通常情況下：【GBDT>=SVM>=RF>=Adaboost>=Other…】