描述：倍增法用於很多演算法當中，通過字面意思來理解就是翻倍增加嘛，這裡著重講使用倍增法在樹中的應用求LCA；

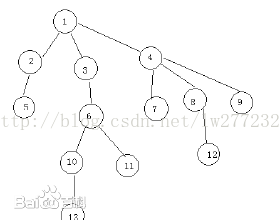
LCA是啥呢  在一棵樹當中 lca表示的是兩個節點最近公共祖先， 大家看這課樹哈節點5 ，3的lca就是1，13和11的LCA就是6。節點8,12的lca就是8，那麼我們如何通過被增來實現LCA呢。

首先請大家認真看下面的分析。

depth[x],表示x節點的深度。

大家看下這個陣列 grand[x][i] ,這個陣列表示標號為x節點向上跳2^i步的節點。例如grand[5][0]=2，因為5這個節點向上跳2^0次方個就是2，當然所有節點向上跳一個就是他的父親節點，

得到grand[x][0]=他的爸爸

那grand[x][1]=什麼呢？等於grand[grand[x][0]][0];

既grand[x][i]=grand[grand[x][i-1]][i-1],為什麼呢，2^4=2^3+2^3,表示 x向上跳2的i次的節點=x向上跳i-1次方的這個節點向上跳i-1次方，有點繞口。例如 grand[13][2]=grand[6][2]=g[g[rand][i-1]][i-1];

有了這個預處理那我們是不是可以得到每一個節點向上跳i格呢，然後就是i的取值範圍為1<=i<=log2(n),向下取整n表示節點個數，也就是說grand[x][log2(n)]就至少可以跳到根節點甚至上面，當然上面啥都沒有。

我們這裡還有一個數組 gw[x][i],表示x節點向上跳2^i次方的距離（權）。同樣的有gw[x][i]=gw[x][i-1]+gw[grand[x][i-1]][i-1],這個公式表示x到他向上跳2的i次方那個節點的距離=x跳2^i-1次方的距離加上，他向上跳2^i-1次方這個點到他上面跳2^i-1次方的距離。

例如1,3,6,10,13，他們之間的邊的權等於 2 4 3 6,既gw[13][0]=他爸爸10到他的距離等於6，gw[]13[2]=gw[13][1]+gw[6][1];。

其實我們可以自己加很多類似的陣列

例如max[x][i]啊表示 x向上跳2^i次方的邊的最大的那條邊。這裡就不一一舉例子子了

現在有了這些預處理。我下面是用dfs實現的預處理；

就看如何實現LCA了吧，

首先 給定兩個節點。假如給定的是a=13，b=12.。要我們求他們的lca ，首先第一步 我們要把他們調整到同一深度，既把a向上跳一個步這樣他們的深度就相同的了。我們是把深度高的向上調。調整跟深度低的一樣。

然後就兩個節點一起向上跳一個2^j，首先我們j從log2(n)=3開始跳，跳到0。我們要跳到他們lca的下面兩個節點。既3和4，既可以跳的節點是他們不相同並且不超出根節點(grand[a][j]!=grand[b][j])，這裡是j=1的時候跳了，j=1因為(grand[a][j]!=grand[b][j]);就執行（a=grand[a][j],b=grand[b][j]）a就跳到了3,b就跳到了4，其餘的j就不可以跳因為j=3，2就到根的上面了j=0他們就想等了。跳到那，最後退出，grand[a][0]就是他們的lca了。

這就是程式的執行過程。下面看程式碼

模板體 ：hdu2586

程式碼：

#include<stdio.h>
#include<string.h>
#include<vector>
#include<stdlib.h>
#include<math.h>
#define max 40001
#define maxl 25
using namespace std;
typedef struct
{
    int from,to,w;
}edge;//這個結構體用來儲存邊

vector<edge>edges;
vector<int> G[max];
//儲存邊的陣列
int grand[max][maxl],gw[max][maxl];//x向上跳2^i次方的節點，x到他上面祖先2^i次方的距離
int depth[max];//深度
int n,m,N;
void addedge(int x,int y,int w)//把邊儲存起來的函式
{
   edge a={x,y,w},b={y,x,w};
   edges.push_back(a);
   edges.push_back(b);

   G[x].push_back(edges.size()-2);
   G[y].push_back(edges.size()-1);
}
void dfs(int x)//dfs建圖
{
    for(int i=1;i<=N;i++)//第一個幾點就全部都是0咯，第二個節點就有變化了，不理解的話建議複製程式碼輸出下這些陣列

    {
        grand[x][i]=grand[grand[x][i-1]][i-1];
        gw[x][i]=gw[x][i-1]+gw[grand[x][i-1]][i-1];
       // if(grand[x][i]==0) break;
    }

    for(int i=0;i<G[x].size();i++)
    {   edge  e = edges[G[x][i]];
         if(e.to!=grand[x][0])//這裡我們儲存的是雙向邊所以與他相連的邊不是他父親就是他兒子父親的話就不能執行，不然就死迴圈了。

           {
                depth[e.to]=depth[x]+1;//他兒子的深度等於他爸爸的加1
                grand[e.to][0]=x;//與x相連那個節點的父親等於x
                gw[e.to][0]=e.w;//與x相連那個節點的距離等於這條邊的距離
                dfs(e.to);//深搜往下面建
           }
    }
}
void Init(){
    //n為節點個數
    N = floor(log(n + 0.0) / log(2.0));//最多能跳的2^i祖先
    depth[1]=0;//根結點的祖先不存在，用-1表示
    memset(grand,0,sizeof(grand));
    memset(gw,0,sizeof(gw));
    dfs(1);//以1為根節點建樹

}
int lca(int a,int b)
{ if(depth[a] > depth[b]) swap(a, b);//保證a在b上面，便於計算
    int ans = 0;
    for(int i = N; i >= 0; i--) //類似於二進位制拆分，從大到小嚐試
        if(depth[a] < depth[b] && depth[grand[b][i]] >= depth[a])//a在b下面且b向上跳後不會到a上面
            ans +=gw[b][i], b=grand[b][i];//先把深度較大的b往上跳

    for(int j=N;j>=0;j--)//在同一高度了,他們一起向上跳,跳他們不相同節點，當全都跳完之後grand【a】【0】就是lca,上面有解釋哈。
    {
        if(grand[a][j]!=grand[b][j])
        {   ans+=gw[a][j];
            ans+=gw[b][j];
            a=grand[a][j];
            b=grand[b][j];

        }
    }
    if(a!=b)//a等於b的情況就是上面土色字型的那種情況
    {
        ans+=gw[a][0],ans+=gw[b][0];
    }
    return ans;
}
int main()
{ int t ;
  scanf("%d",&t);
  while(t--)
  {   scanf("%d%d",&n,&m);
      for(int i=1;i<n;i++)
      {
          int x,y,w;
          scanf("%d%d%d",&x,&y,&w);
          addedge(x,y,w);
      }
     Init();
     for(int i=1;i<=m;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         printf("%d\n",lca(x,y));
     }
  }
}