葉子結點：一棵樹當中沒有子結點（即度為0）的結點稱為葉子結點，簡稱“葉子”。

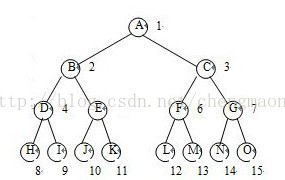
如圖所示：

高度

對於高度的理解，我們不管他資料結構什麼什麼知識，就拿樓房來說，假如一個人提問：樓房的高度有好高？我們會下意識的從底層開始往上數，假如樓有6層，則我們會說，這個樓有6層樓那麼高，則提問者就會大概知道樓有多高了。所以高度就是以從下往上對比，這是我們的習慣。而在樹中，樹的高度也是從下往上數，如圖所示

K節點在樹的底層，是一個葉子節點，則一般定義為K的高度在最低為1，以此類推，O的高度也是為1，P的節點也是為1。M節點是葉子節點O的父節點，從下往上數，M節點高度為2。那麼G節點的高度是多少呢？從G-L的高度為2，從G-M-O節點高度為3，到底G節點高度為多少呢，正確答案是3，請看定義：

高度的定義為：從結點x向下到某個葉結點最長簡單路徑中邊的條數

深度：

理解了高度，則深度的理解就很容易了，深度是從根節點往下，列如上圖中：B的深度為2。

結點的深度：從根節點開始自頂向下逐層累加。

深度與高度差異：

對於整棵樹來說，最深的葉結點的深度就是樹的深度；樹根的高度就是樹的高度。這樣樹的高度和深度是相等的。

 對於樹中相同深度的每個結點來說，它們的高度不一定相同，這取決於每個結點下面的葉結點的深度。

B樹的目的為了硬碟快速讀取資料（降低IO操作次樹）而設計的一種平衡的多路查詢樹。目前大多資料庫及檔案索引，都是使用B樹或變形來儲存實現。

為什麼B樹效率高:

在大規模資料儲存操作中，由於無法一次性載入到記憶體裡。所以避免不了發生內外存交換。所以次數越少，效率表現也越高。

b+樹來儲存，只有葉子節點儲存資料，每個葉子節點都指向下一個。

 B樹：二叉樹，每個結點只儲存一個關鍵字，等於則命中，小於走左結點，大於

走右結點；

       B-樹：多路搜尋樹，每個結點儲存M/2到M個關鍵字，非葉子結點儲存指向關鍵

字範圍的子結點；

       所有關鍵字在整顆樹中出現，且只出現一次，非葉子結點可以命中；

       B+樹：在B-樹基礎上，為葉子結點增加連結串列指標，所有關鍵字都在葉子結點

中出現，非葉子結點作為葉子結點的索引；B+樹總是到葉子結點才命中；

       B*樹：在B+樹基礎上，為非葉子結點也增加連結串列指標，將結點的最低利用率

從1/2提高到2/3；

滿二叉樹

一棵深度為k，且有2^k-1個節點的樹是滿二叉樹。

另一種定義：除了葉結點外每一個結點都有左右子葉且葉子結點都處在最底層的二叉樹。

這兩種定義是等價的。

從樹的外形來看，滿二叉樹是嚴格三角形的，大家記住下面的圖，它就是滿二叉樹的標準形態：

所有內部節點都有兩個子節點，最底一層是葉子節點。

性質：

1)        如果一顆樹深度為h，最大層數為k，且深度與最大層數相同，即k=h;

2)        它的葉子數是： 2^(h-1)

3)        第k層的結點數是： 2^(k-1)

4)        總結點數是： 2^k-1 (2的k次方減一)

5)        總節點數一定是奇數。

6)        樹高：h=log2(n+1)。

完全二叉樹

完全二叉樹是由滿二叉樹而引出來的。對於深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。

若設二叉樹的深度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第h 層所有的結點都連續集中在最左邊，這就是完全二叉樹。

（大家好好理解一下上面兩個定義，是等價的~~）

滿二叉樹一定是完全二叉樹，完全二叉樹不一定是滿二叉樹。

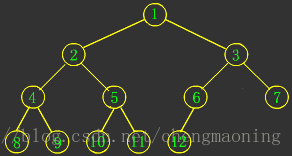
下面是完全二叉樹的基本形態：

完全二叉樹的性質：

1)        深度為k的完全二叉樹，至少有2^(k-1)個節點，至多有2^k-1個節點。

2)        樹高h=log2n + 1。

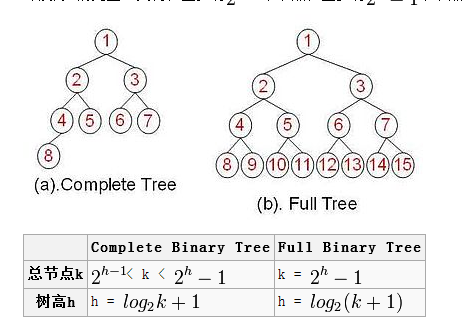
對滿二叉樹、完全二叉樹總結點及樹高的總結：