牛頓迭代法流程圖：

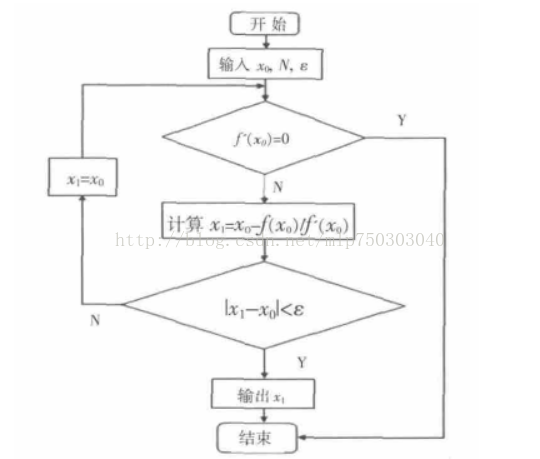
Newton迭代法計算步驟 ：

（1） 取初始點x0，最大迭代次數N和精 度 ε。

（2） 如果 f' (x0)=0， 則停止計算；否則計算  x1 = x0 -f（x0）/ f'（x0）。

（3） 如果|x1-x0|＜ε， 則停止計算 ； 否 則 x0=x1， 轉 到 （2）。

（4） 如果n=N， 則停止計算； 否 則 取 n=n+1， 轉 到 （2）。

function f=fun(x);  %定義非線性方程組  
syms x1 x2  x3  x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15
p=1025;
g=9.8;
f1=-p*g*x1*pi+12000+sin(x2)*x3;
f2=-x3*cos(x2)+0.625*pi*(2-x1)*12*12;

f3=-x3*sin(x2)-pi*0.025*0.025*p*g+100+x(5)*sin(x6);
f4=-x3*cos(x2)+x5*cos(x6);

f5=-x5*sin(x6)-pi*0.025*0.025*p*g+100+x7*sin(x8);
f6=-x5*cos(x6)+x7*cos(x8);

f7=-x7*sin(x8)-pi*0.025*0.025*p*g+100+x9*sin(x10);
f8=-x7*cos(x8)+x9*cos(x10);

f9=-x9*sin(x10)-pi*0.025*0.025*p*g+100+x11*sin(x12);
f10=-x9*cos(x10)+x(11)*cos(x12);
a=0.625*12*12*pi*(2-x1);
f11=-0.15*0.15*p*g-x11*sin(x12)+1000+0.625*12*12*pi*(2-x1)*cosh(x13/a)*sin(x14)+12000;
f12=-x11*cos(x12)+0.625*12*12*pi*(2-x1)*cosh(x13/a)*cos(x14);
f14=-x1-(sin(x2)+sin(x6)+sin(x8)+sin(x10)+sin(x12))-x15+18;
f15=-x15+a-cosh(x13/a-1);
f16=-p*(pi*x(1)+0.025*0.025*pi*4+0.15*0.15*pi)+1000+40+100+1200;
f17=-cos(x14)+1/cosh(x13/a);
f=[f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f14 f15 f16 f17];
  
 

function df=dfun1(x)  %雅克比矩陣 
f=fun(x);  
df=[diff(f,'x1');diff(f,'x2');diff(f,'x3');diff(f,'x5');diff(f,'x6');diff(f,'x7');diff(f,'x8');diff(f,'x9');diff(f,'x10');diff(f,'x11');diff(f,'x12');diff(f,'x13');diff(f,'x14');diff(f,'x15')];  

clear;clc  
format;  
x0=[0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1];   % 迭代初始值  
eps = 0.0001;  % 定位精度要求  
for i = 1:1000 
    f = double(subs(fun(x0),{'x1' 'x2'  'x3'  'x5' 'x6' 'x7' 'x8' 'x9' 'x10' 'x11' 'x12' 'x13' 'x14' 'x15'},{x0(1) x0(2) x0(3) x0(4) x0(5) x0(6) x0(7) x0(8) x0(9) x0(10) x0(11) x0(12) x0(13) x0(14) }));  
    df = double(subs(dfun1(x0),{'x1' 'x2'  'x3'  'x5' 'x6' 'x7' 'x8' 'x9' 'x10' 'x11' 'x12' 'x13' 'x14' 'x15'},{x0(1) x0(2) x0(3) x0(4) x0(5) x0(6) x0(7) x0(8) x0(9) x0(10) x0(11) x0(12) x0(13) x0(14)}));  % 得到雅克比矩陣  
    x = x0 - f/df;  
    if(abs(x-x0) < eps)  
        break;  
    end  
    x0 = x; % 更新迭代結果  
end  
disp('定位座標：');  
x  
disp('迭代次數：');  
i