最近在幫學弟做一個關於OCR的專案，所以這幾個星期都沒有在CSDN上更新文章。今天登入後發現有還幾個小夥伴關注我了，很開心~。我會繼續在CSDN上更新一些內容，總結自己每個階段的學習情況。
周志華老師的西瓜書堪稱學習機器學習的必備書籍，很多學生包括我自己都是從這本書開始接觸機器學習。周志華老師將這本書定位一本自學用書和科研參考書，但對於初學者來說，在學這本書的時候肯定有很多不明白的地方。我大概在去年的十月份開始接觸這本書，當時學業壓力比較大，只是大體上對這本書進行翻閱，沒有深入思考，以至於現在對這本書的理解還是非常淺薄。為此我進行本系列文章的寫作，一遍學一遍總結，我會盡自己最大的努力去推導書中的公式。
當然，我寫的這些文章肯定也存在一些認識不夠到位的地方，希望可以和大家多交流。謹以此作為自己學習的總結，並作為一個和大家進行交流的平臺。

本章是全書的第一章，作者在這一章節主要介紹了一些機器學習中常用的概念和原理，並總結回顧機器學習的發展歷程，氣提綱挈領的作用，總體來說這一部分難度並不大。

1.1 引言

這一部分主要講解了什麼是機器學習，周志華老師在這裡舉了很多例子來幫助我們進行理解。

1、經驗： 在生活中，我們存在很多用經驗來做判斷的事情，比如挑西瓜、用生活常識來判斷明天的天氣等，在計算機系統中，這些經驗用"資料”來進行表示，一條資料就是一個經驗。

2、機器學習的任務： 關於計算機從資料中產生“模型”的演算法，也就是我們經常說的學習演算法。有了這個模型，我們就可以將資料輸入其中從而得到判斷結果。

3、機器學習的形式化定義：

假設用P來評估計算機程式在某一個任務類T上的效能，若一個程式通過利用經驗E在T中任務上獲得了效能改善，則我們就說關於T和P，該程式對E進行了學習。

1.2 基本術語

這裡是對一些基本術語的介紹：
1、屬性： 反映事件或物件在某方向的表現或性質，也稱為特徵。如西瓜的“色澤”、“敲聲”等。
2、屬性值： 顧名思義，屬性的取值就稱為屬性值，如“青綠”、“烏黑”等。
3、屬性空間： 屬性張成的空間稱為屬性空間，也稱為樣本空間或者“輸入空間”。如把“色澤”、“根蒂”、“敲聲”作為三個座標軸，則他們張成一個描述西瓜的三維空間，每個西瓜都可以在這個空間中找到自己的座標位置。由於空間中每個點都對應一個座標向量，所以我們也在一個例項稱為一個“特徵向量”。
4、資料集:

一組記錄的集合稱為資料集。
5、樣本： 其中每一條記錄是關於一個事件或物件的描述，稱為示例或樣本，例如：（色澤=青綠；根蒂=稍蜷；敲聲=沉悶）
6、學習： 從資料中學得模型的過程稱為學習，這個過程一般通過執行某個學習演算法來完成，也稱為訓練。
7、訓練資料： 訓練過程中使用的資料稱為訓練資料。
8、訓練樣本： 訓練過程的每個樣本稱為訓練樣本。
9、訓練集： 由訓練樣本組成的集合稱為訓練集。
10、假設： 學得模型對應了關於資料的某種潛在的規律,即hypothesis，這個英文名我們會在後續文章中繼續用到。
11、學習器： 其實學習的過程是為了找出或者逼近真相，所以我們有時候也把模型稱為“學習器”，可看作學習演算法在給定資料和引數空間上的例項化。
12、標記（label）： 想要學得一個模型，僅有已有的示例資料是不夠的。要建立一個關於預測的模型，需要獲得訓練樣本的“結果”資訊。例如“（（色澤=青綠；根蒂=稍蜷；敲聲=濁響），好瓜）”。這裡關於示例結果的資訊“好瓜”，就稱為標記。
13、分類： 如果我們預測的值是離散值，如“好瓜”、“壞瓜”，這一類學習任務就稱為分類。
14、迴歸： 如果我們預測的值是連續值，例如西瓜的成熟度0.95,0.37，則我們稱此類學習任務為迴歸。
15、監督學習（supervised learning）： 訓練的資料既有特徵又有標籤(，通過訓練，典型代表是分類和迴歸。
16、無監督學習（unsupervised learning）： 訓練的資料沒有標籤存在，通過資料之間的內在聯絡和相似性將他們分成若干類。典型代表為聚類。
17、泛化能力： 我們學的模型可以適用於新樣本的能力稱為泛化能力，具有強泛化能力的模型可以很好的適用於整個樣本空間。
18、獨立同分布： 假設樣本空間中全體樣本服從一個未知的“分佈”D，我們獲得的每個樣本都是獨地從這個分佈上取樣獲得的，即“獨立同分布”。

1.3 假設空間

歸納（induction）和演繹（deduction）是科學推理的兩大基本手段。

• 歸納（induction）： 從特殊到一般的“泛化”過程。即從具體的事實歸結出一般性規律
• 演繹（deduction）： 從一般到特殊的“特化”（specialization）過程。即從基礎原理推演出具體的情況

歸納學習有狹義和廣義之分，廣義的歸納學習大體相當於從樣例中進行學習，而狹義的歸納學習則要求從訓練資料中學得概念，因此也稱為"概念學習"或者“概念生成”。

概念學習中最基本是“布林概念學習”，即對“是”、“不是”主要可以表示為0/1的布林值的目標概念的學習。

我們可以把學習過程看做是一個在所有的假設（hypothesis）組成的空間中進行搜尋的空間，搜尋目標是找到與訓練集“匹配”（fit）的假設，即能夠將訓練集中的瓜判斷正確的假設。假設一旦確定，假設空間及其規模大小就確定了。

我們以西瓜問題的假設空間為例來對這一部分進行說明：西瓜的色澤、根蒂和淺白均有三個可能的取值，除此以外，還有一個取任何值均合適的引數“ * "，所以我們面臨的假設空間規模大小為 $4\times4\times4+1=65$

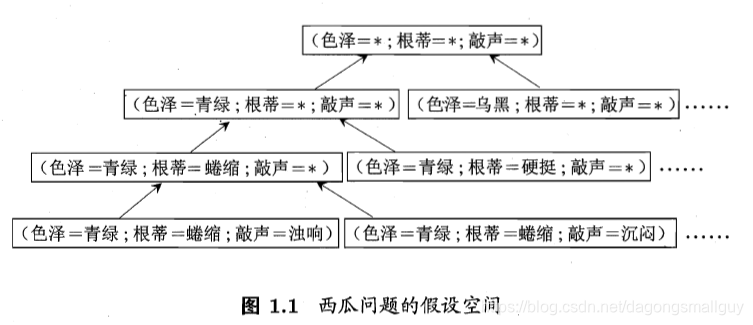
我們可以有很多策略對這個假設空間進行搜尋，例如自頂向下，從一般到特殊，或是自底向上，從特殊到一般，搜尋過程中可以不用不斷刪除與正例不一致的假設，和與反例一致的假設，最紅將會得到與訓練集一致（即對所有的訓練樣本能夠進行正確判斷）的假設，這就是我們學的得的結果。

在現實問題中，我們有時候會面臨很大的假設空間，但是學習過程是基於有限樣本集進行的。因此可能有多個假設與訓練集一致，即存在著一個與訓練集一致的“假設集合”，我們稱之為“版本空間”。

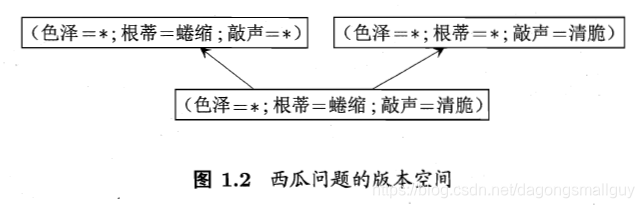
1.4 歸納偏好

通過學習得到的模型可以對應假設空間中的一個假設。但是上文版本空間的有關知識告訴我們，當存在多個假設時，不同的假設有不同的輸出，這顯然不符合我們的期望。

我們把機器學習演算法在學習過程中對某種型別的偏好就稱為“歸納偏好”，或者簡稱為“偏好”。任何一個有效的機器學習演算法都必須要有偏好，否則會被假設空間中的看似在訓練集中“等效”的假設所迷惑從，從而產生無法確定的結果。

歸納偏好對應了學習計演算法本身所作的關於“什麼樣的模型更好的假設”，在具體的現實問題中，這個假設是否成立。即演算法的歸納偏好是否與問題本身匹配，大多數情況下直接決定了演算法能否取的很好的效能。

“奧卡姆剃刀”為我們提供了一種常用的，自然科學研究種最基本的法則，可以用來引導演算法確立“正確”的偏好。即“若有多個假設與觀察一致，則選擇最簡單的那個”。

根據“奧卡姆剃刀”法則，對於如下兩個演算法A和B，我們根據平滑曲線的某種“描述簡單性”希望演算法A的效能比演算法B更好。左圖的結果顯示：與B相比，A與訓練集外的樣本更一致，換言之，A的泛化能力比B強。但是右圖的結果顯示演算法B的效能更好，這種情況也有可能出現。

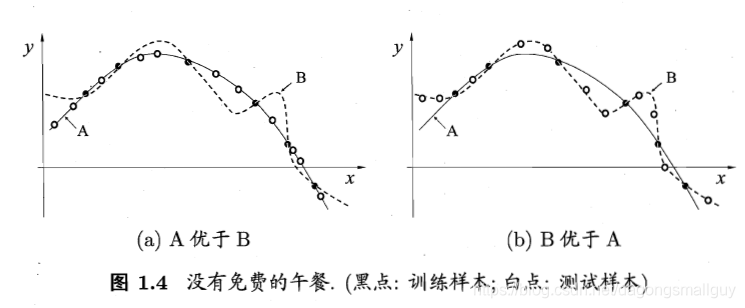
接下來，我們用簡單的數學公式對以上理論進行說明。

我們假設樣本空間 $\chi$和假設空間 $H$都是離散的，令 $P\left ( h|X,\varepsilon _{a} \right )$代表演算法 $\varepsilon _{a}$基於訓練資料 $X$產生假設 $h$的概率，再令 $f$代表我們希望學習的真實函式。
則 $\varepsilon _{a}$的“訓練集外誤差”，即 $\varepsilon _{a}$在訓練集外的所有樣本上的誤差為：

在這個公式中， $P(x)$為函式 $x$本身的概率，我們用指示函式選出與真實函式不同的那一部分，然後將其乘以h相應的概率，因為在這裡我們提出的h不止一個，我們需要對所有的h的誤差進行求和。

對於二分類問題，當它的真實函式可以是任何函式 $\chi$都在0到1之間時，我們對所有可能的f按均勻分佈對誤差求和，有：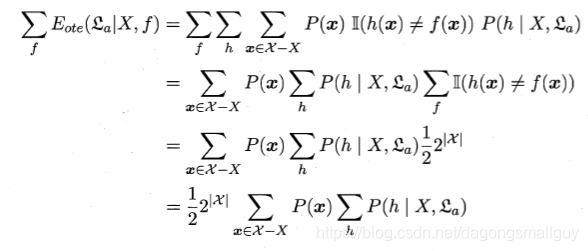

我們將上式化簡得：

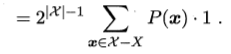
對於上式我們需要做如下解釋，若 $f$均勻分佈，則我們有一般的 $f$對 $x$的預測與 $h$不一致。所以在二分類問題中，當樣本數為 $\chi$時，我們有 $2^{\left | \chi \right |}$個對 $f$的預測，其中一半不符合，所以我們有：

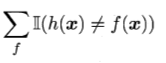
等於 $\frac{1}{2}\times 2^{\left | \chi \right |}$

我們從這個式子裡面發現似乎總誤差與具體選擇哪個學習演算法無關， 這與我們的生活常識產生矛盾。無論一個演算法多麼笨拙，無論一個演算法多麼聰明，他們的期望效能相同，這個就是我們常說的“沒有免費的午餐”定理。

但是在推匯出這個結果之前，我們假設 $f$d均勻分佈，所有問題的出現機會都相同，或者所有的問題都同等重要，這與我們的事實發生矛盾。

NFL定理其實最想告訴我們的，是脫離具體的問題空談什麼演算法最好毫無意義，考慮所有的潛在問題，則所有的學習演算法都一樣好，要談論具體演算法的好壞，必須要引入具體的問題。

1.5 發展歷程

20世紀80年代，“從樣例中學習”的一大主流師符號主義學習，其代表包括決策樹和基於邏輯學習。

20世紀90年代中期之前，“從樣例中學習”的另一主流技術是基於神經網路的連線主義學習。

20世紀90年代中期, “統計學習（statistical learning）”閃亮登場並迅速佔據主流舞臺，代表技術是支援向量機（Support Vector Machine,簡稱SVM）以及更一般的“核方法”（kernel methods）

21世紀初，連線主義捲土重來，掀起了以“深度學習”為名的熱潮。深度學習的前身是連線主義學習