題目連線：

一定要見雙向邊，第二次了…………………………。因為這兩邊的點是一樣的

題目：

描述

國慶期間正是旅遊和遊玩的高峰期。

小Hi和小Ho的學習小組為了研究課題，決定趁此機會派出若干個調查團去沿途檢視一下H市內各個景點的遊客情況。

H市一共有N個旅遊景點(編號1..N)，由M條單向遊覽路線連線。在一個景點遊覽完後，可以順著遊覽線路前往下一個景點。

為了避免遊客重複遊覽同一個景點，遊覽線路保證是沒有環路的。

每一個調查團可以從任意一個景點出發，沿著計劃好的遊覽線路依次調查，到達終點後再返回。每個景點只會有一個調查團經過，不會重複調查。

舉個例子：

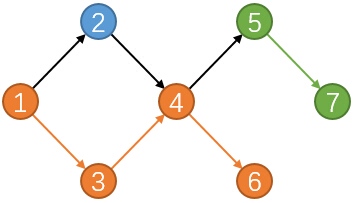
上圖中一共派出了3個調查團：

1. 藍色：調查景點；2

2. 橙色：調查景點；1->3->4->6

3. 綠色：調查景點；5->7

當然對於這個圖還有其他的規劃方式，但是最少也需要3個調查團。

由於小組內的人數有限，所以大家希望調查團的數量儘可能少，同時也要將所有的景點都進行調查。

當然，如何規劃調查團線路的任務落到了小Hi和小Ho的頭上。

提示：最小路徑覆蓋

輸入

第1行：2個整數N,M。1≤N≤500,0≤M≤20,000。

第2..M+1行：2個數字u,v，表示一條有向邊(u,v)。保證不會出現重複的邊，且不存在環。

輸出

第1行：1個整數，表示最少需要的調查團數量。

樣例輸入

7 7
1 2
1 3
2 4
3 4
4 5
4 6
5 7

樣例輸出

3

解法：

小Ho：所以這一次我們應該如何來解決這個問題呢？

小Hi：嗯，這次的問題被稱為最小路徑覆蓋。給定一個有向無環圖，用最少的路徑數量去保證所有點都被覆蓋住。

小Ho：既然有名字，那一定有固定的解法了？

小Hi：沒錯，最小路徑覆蓋的結果等於N-最大二分匹配。

小Ho：二分匹配？這和二分匹配有什麼關係？給定的有向圖不一定是二分圖吧。

小Hi：當然不是在原圖上進行的二分匹配了。我們需要對原圖進行轉化，同時這一次我們還要學習如何用網路流去解決二分匹配的問題。

小Ho：好，你快給我講講。

小Hi：好的好的，你別急。我們先從例子來分析：

在這個例子中，我們選擇的三條路徑都被染上了顏色。你有發現什麼特殊之處麼？

小Ho：嗯...<小Ho思考了一小會兒>...並沒有什麼特別的地方啊？

小Hi：把黑色的邊去掉，你再看看呢？主要注意的是每個點的出入度數量。

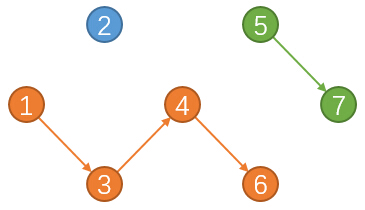
小Ho：對於一條路徑，起點的入度為0，終點的出度為0，中間節點的出入度都為1。但這不是路徑都應該具有的性質麼？

小Hi：這個性質就是我們解決題目的關鍵！

每一個點最多隻能有1個後繼，同時每一個點最多隻能有1個前驅。

假如我們選擇了一條邊(u,v)，也就等價於把前驅u和後繼v匹配上了。這樣前驅u和後繼v就不能和其他節點匹配。

小Ho：那就是一個前驅匹配一個後繼？

小Hi：是的，利用這個我們可以這樣來構圖：

將每一個點拆分成2個，分別表示它作為前驅節點和後繼節點。將所有的前驅節點作為A部，所有後繼節點作為B部。

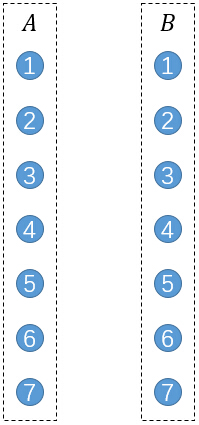
接下來進行連邊，若原圖中存在一條邊(u,v)，則連線A部的u和B部的v。

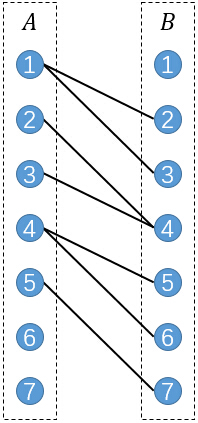
那麼小Ho，你在這個上面做一個最大二分匹配怎麼樣？

小Ho：好！......完成了。

小Hi：不錯，讓我再把對應的顏色染出來：

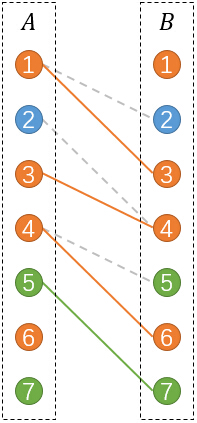
其中實線表示被選中的匹配，虛線表示未被選中的。

有沒有發現，和原圖剛好有著對應的關係。未被選中的匹配也正好對應了原圖中我們沒有選擇的黑色邊。

小Ho：是的呢？這是為什麼呢？

小Hi：其實原理很簡單。我們進行的匹配是前驅和後繼的匹配。假如存在選中的匹配(i,j)和(j,k)。則表示原圖中存在一條路徑(i,j,k)。

比如例子中的匹配(1,3),(3,4),(4,6)就對應了原圖中的路徑(1,3,4,6)。

這樣在匹配結束的時候，我們就可以直接通過匹配的情況來確定選中的路徑。

小Ho：這個我懂了，但是如何保證這樣就能得到最小的路徑覆蓋呢？

小Hi：你想想，每一條路徑起點有什麼特殊的地方？

小Ho：路徑的起點入度為0...哦！我知道了。

如果一個點是路徑起點的話，它在B部的節點一定是沒有匹配上的。

經過最大匹配演算法後，B部剩下沒有被匹配的點一定是最少的，也就對應了最小需要的路徑數。

所以最小路徑覆蓋的結果才是N-最大匹配數。

小Hi：正是這樣，這樣問題也就解決了。接下來第二個問題，怎麼用網路流來解決二分匹配呢？

小Ho：上一次我們講了二分多重匹配，二分匹配不就是它的簡化版麼。

只需要把源點s到A部的邊和B部到匯點t的邊容量限定為1就可以了！

小Hi：嗯，那麼就只差最後一步了。

小Ho：這我也知道！實現嘛，交給我

程式碼：

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <stdlib.h>
#include <iomanip>
#include <fstream>

using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define maxn 1010
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define mem(a , b) memset(a , b , sizeof(a))
#define LL long long
#define ULL unsigned long long
#define FOR(i , n) for(int i = 1 ;  i<= n ; i ++)
typedef pair<int , int> pii;
int n , m , ed;
vector<int>v[maxn];
int vis[maxn] , path[maxn] , a[maxn][maxn];
int flow[maxn] , ans;

bool BFS()
{
    mem(vis , 0);
    mem(path , -1);
    mem(flow , 0);
    queue<int>q;
    while(!q.empty()) q.pop();
    q.push(0);
    vis[0] = 1;
    flow[0] = INF;
    while(!q.empty())
    {
        int cur = q.front();
        q.pop();
        if(cur == ed) return 1;
        for(int i = 0 ; i < v[cur].size() ; i ++)
        {
            if(!vis[v[cur][i]] && a[cur][v[cur][i]] > 0)
            {
                vis[v[cur][i]] = 1;
                flow[v[cur][i]] = min(flow[cur] , a[cur][v[cur][i]]);
                path[v[cur][i]] = cur;
                q.push(v[cur][i]);
            }
        }
    }
    return 0;
}

int main()
{
    while(scanf("%d %d" , &n , &m) != EOF)
    {
        int s , to;
        mem(a , 0);
        ed = n + n + 1;
        for(int i = 0 ; i < m ; i ++)
        {
            scanf("%d %d" , &s , &to);
            v[s].push_back(to + n);
            v[to+n].push_back(s);
            a[s][to+n] = 1;
        }
        for(int i = 1 ; i <= n ; i ++)
        {
            v[0].push_back(i);
            v[i].push_back(0);
            a[0][i] = 1;
            v[i+n].push_back(ed);
            v[ed].push_back(i+n);
            a[i+n][ed] = 1;
        }
        ans = 0;
        while(BFS())
        {
            ans += flow[ed];
            int fir = ed , sec = path[fir];
            while(sec != -1)
            {
                a[fir][sec] += flow[ed];
                a[sec][fir] -= flow[ed];
                fir = sec;
                sec = path[fir];
            }
        }
        printf("%d\n" , n - ans);
    }
    return 0;
}