最大矩形面積(單調棧解法,我在此題探索到了許多)
目錄
》題目《
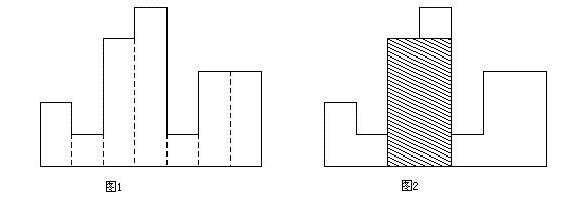
在X軸上水平放置著 N 個條形圖,這 N 個條形圖就組成了一個柱狀圖,每個條形圖都是一個矩形,每個矩形都有相同的寬度,均為1單位長度,但是它們的高度並不相同。例如下圖,圖1包含的矩形的高分別為2,1,4,5,1,3,3 單位長度,矩形的寬為1單位長度。
你的任務就是計算柱狀圖中以X軸為底邊的最大矩形的面積。圖2陰影部分就是上述例子的最大矩形面積
》輸入《
輸入資料的第一行是一個整數 N(1≤ N ≤100000),表示柱狀圖包含 N 個矩形。緊接著 N 個整數h1,...,hn(0≤ hi ≤20000, 1≤ i≤ N),表示柱狀圖中按從左到右順序給出的矩形的高度。矩形的寬度為1。
》輸出《
最大矩形的面積
》樣例輸入《
7
2 1 4 5 1 3 3
》樣例輸出《
8
》思路《
大多數讀者一眼就看出了這是最大矩形,怎麼搞?怎麼搞?
首先,我們思考一下每個矩形是如何來的
是不是以每棟建築的高度為矩形的一邊,再尋找另一邊的長度(是的)
如何尋找另一邊呢?
是不是左邊第一個比這個建築低的位置(左邊界)到右邊第一個比這個建築低的位置 (右邊界)之間的距離(翻回去看,是不是?)
如何搞?
單調佇列就很有用了。
首先,如果這個元素要入隊(必須進去,別問我為什麼),就要維護此佇列的單調性(從棧底到棧頂(非)遞增(減))
這道題就要用遞增序列了(為什麼後面會講)
怎麼求左邊界呢?
試想:h[i-1] > h[i],是不是以 h[i-1] 為一邊的矩形的右邊界已經確定(因為已經不可能再往右延伸了嘛)
那麼以 h[i] 為一邊的矩形的左邊界就要向左移一位(即 h[i] 的右邊界更新成 i-1)
而這時 h[i-1] 已經已經沒用了,所以我們就可以計算以 h[i-1] 為一邊的矩形的面積,而它的右邊界是不是就是 h[i] 的位置?
以它為一邊的矩形的面積是不是就是 (h[i]的位置 - h[i-1]的位置)*h[i]。
所以,每當後一個建築的高度小於前一個的高度時,就要把前一個建築彈出去,更新位置(是不是單調遞增的?)
至於細節嘛,自己想(cuo)去吧
》程式碼《
#include <stack>
#include <cstdio>
#include <iostream>
using namespace std;
struct node{
int p, zhi;
}a[100005], b;
stack<node> t;
int ans, n;
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i ++){
scanf("%d", &a[i].zhi);
a[i].p = i;
}
t.push(a[1]);
for(int i = 2; i <= n; i ++){
int pp = a[i].p;
while( !t.empty() && t.top().zhi > a[i].zhi ){
b = t.top();
t.pop();
a[i].p = b.p;
int big = (pp - b.p) * b.zhi;
ans = max(big ,ans);
}
t.push(a[i]);
}
while( !t.empty() ){
b = t.top();
t.pop();
int big = (n + 1 - b.p) * b.zhi;
ans = max(big ,ans);
}
printf("%d\n",ans);
return 0;
}
歡迎讀者補充與交流