Dancing Links演算法——求解精確覆蓋問題
轉載自:http://www.cnblogs.com/grenet/p/3145800.html
精確覆蓋問題的定義:給定一個由0-1組成的矩陣,是否能找到一個行的集合,使得集合中每一列都恰好包含一個1
例如:如下的矩陣
就包含了這樣一個集合(第1、4、5行)
如何利用給定的矩陣求出相應的行的集合呢?我們採用回溯法
先假定選擇第1行,如下所示:
如上圖中所示,紅色的那行是選中的一行,這一行中有3個1,分別是第3、5、6列。
由於這3列已經包含了1,故,把這三列往下標示,圖中的藍色部分。藍色部分包含3個1,分別在2行中,把這2行用紫色標示出來
根據定義,同一列的1只能有1個,故紫色的兩行,和紅色的一行的1相沖突。
那麼在接下來的求解中,紅色的部分、藍色的部分、紫色的部分都不能用了,把這些部分都刪除,得到一個新的矩陣
行分別對應矩陣1中的第2、4、5行
列分別對應矩陣1中的第1、2、4、7列
於是問題就轉換為一個規模小點的精確覆蓋問題
在新的矩陣中再選擇第1行,如下圖所示
還是按照之前的步驟,進行標示。紅色、藍色和紫色的部分又全都刪除,導致新的空矩陣產生,而紅色的一行中有0(有0就說明這一列沒有1覆蓋)。說明,第1行選擇是錯誤的
那麼回到之前,選擇第2行,如下圖所示
按照之前的步驟,進行標示。把紅色、藍色、紫色部分刪除後,得到新的矩陣
行對應矩陣2中的第3行,矩陣1中的第5行
列對應矩陣2中的第2、4列,矩陣1中的第2、7列
由於剩下的矩陣只有1行,且都是1,選擇這一行,問題就解決
於是該問題的解就是矩陣1中第1行、矩陣2中的第2行、矩陣3中的第1行。也就是矩陣1中的第1、4、5行
在求解這個問題的過程中,我們第1步選擇第1行是正確的,但是不是每個題目第1步選擇都是正確的,如果選擇第1行無法求解出結果出來,那麼就要推倒之前的選擇,從選擇第2行開始,以此類推
從上面的求解過程來看,實際上求解過程可以如下表示
1、從矩陣中選擇一行
2、根據定義,標示矩陣中其他行的元素
3、刪除相關行和列的元素,得到新矩陣
4、如果新矩陣是空矩陣,並且之前的一行都是1,那麼求解結束,跳轉到6;新矩陣不是空矩陣,繼續求解,跳轉到1;新矩陣是空矩陣,之前的一行中有0,跳轉到5
5、說明之前的選擇有誤,回溯到之前的一個矩陣,跳轉到1;如果沒有矩陣可以回溯,說明該問題無解,跳轉到7
6、求解結束,把結果輸出
7、求解結束,輸出無解訊息
從如上的求解流程來看,在求解的過程中有大量的快取矩陣和回溯矩陣的過程。而如何快取矩陣以及相關的資料(保證後面的回溯能正確恢復資料),也是一個比較頭疼的問題(並不是無法解決)。以及在輸出結果的時候,如何輸出正確的結果(把每一步的選擇轉換為初始矩陣相應的行)。
於是演算法大師Donald E.Knuth(《計算機程式設計藝術》的作者)出面解決了這個方面的難題。他提出了DLX(Dancing Links X)演算法。實際上,他把上面求解的過程稱為X演算法,而他提出的舞蹈鏈(Dancing Links)實際上並不是一種演算法,而是一種資料結構。一種非常巧妙的資料結構,他的資料結構在快取和回溯的過程中效率驚人,不需要額外的空間,以及近乎線性的時間。而在整個求解過程中,指標在資料之間跳躍著,就像精巧設計的舞蹈一樣,故Donald E.Knuth把它稱為Dancing Links(中文譯名舞蹈鏈)。
Dancing Links的核心是基於雙向鏈的方便操作(移除、恢復加入)
我們用例子來說明
假設雙向鏈的三個連續的元素,A1、A2、A3,每個元素有兩個分量Left和Right,分別指向左邊和右邊的元素。由定義可知
A1.Right=A2,A2.Right=A3
A2.Left=A1,A3.Left=A2
在這個雙向鏈中,可以由任一個元素得到其他兩個元素,A1.Right.Right=A3,A3.Left.Left=A1等等
現在把A2這個元素從雙向鏈中移除(不是刪除)出去,那麼執行下面的操作就可以了
A1.Right=A3,A3.Left=A1
那麼就直接連線起A1和A3。A2從雙向鏈中移除出去了。但僅僅是從雙向鏈中移除了,A2這個實體還在,並沒有刪除。只是在雙向鏈中遍歷的話,遍歷不到A2了。
那麼A2這個實體中的兩個分量Left和Right指向誰?由於實體還在,而且沒有修改A2分量的操作,那麼A2的兩個分量指向沒有發生變化,也就是在移除前的指向。即A2.Left=A1和A2.Right=A3
如果此時發現,需要把A2這個元素重新加入到雙向鏈中的原來的位置,也就是A1和A3的中間。由於A2的兩個分量沒有發生變化,仍然指向A1和A3。那麼只要修改A1的Right分量和A3的Left就行了。也就是下面的操作
A1.Right=A2,A3.Left=A2
仔細想想,上面兩個操作(移除和恢復加入)對應了什麼?是不是對應了之前的演算法過程中的關鍵的兩步?
移除操作對應著快取資料、恢復加入操作對應著回溯資料。而美妙的是,這兩個操作不再佔用新的空間,時間上也是極快速的
在很多實際運用中,把雙向鏈的首尾相連,構成迴圈雙向鏈
Dancing Links用的資料結構是交叉十字迴圈雙向鏈
而Dancing Links中的每個元素不僅是橫向迴圈雙向鏈中的一份子,又是縱向迴圈雙向鏈的一份子。
因為精確覆蓋問題的矩陣往往是稀疏矩陣(矩陣中,0的個數多於1),Dancing Links僅僅記錄矩陣中值是1的元素。
Dancing Links中的每個元素有6個分量
分別:Left指向左邊的元素、Right指向右邊的元素、Up指向上邊的元素、Down指向下邊的元素、Col指向列標元素、Row指示當前元素所在的行
Dancing Links還要準備一些輔助元素(為什麼需要這些輔助元素?沒有太多的道理,大師認為這能解決問題,實際上是解決了問題)
Ans():Ans陣列,在求解的過程中保留當前的答案,以供最後輸出答案用。
Head元素:求解的輔助元素,在求解的過程中,當判斷出Head.Right=Head(也可以是Head.Left=Head)時,求解結束,輸出答案。Head元素只有兩個分量有用。其餘的分量對求解沒啥用
C元素:輔助元素,稱列標元素,每列有一個列標元素。本文開始的題目的列標元素分別是C1、C2、C3、C4、C5、C6、C7。每一列的元素的Col分量都指向所在列的列標元素。列標元素的Col分量指向自己(也可以是沒有)。在初始化的狀態下,Head.Right=C1、C1.Right=C2、……、C7.Right=Head、Head.Left=C7等等。列標元素的分量Row=0,表示是處在第0行。
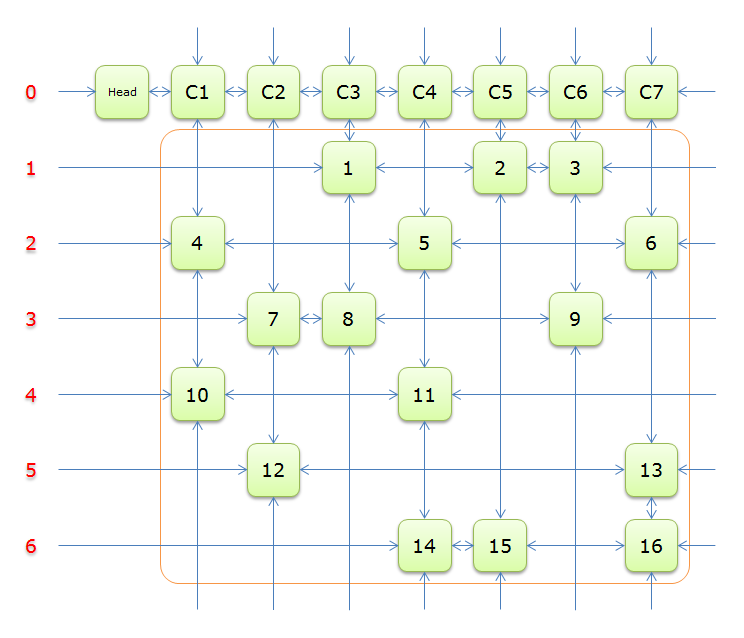
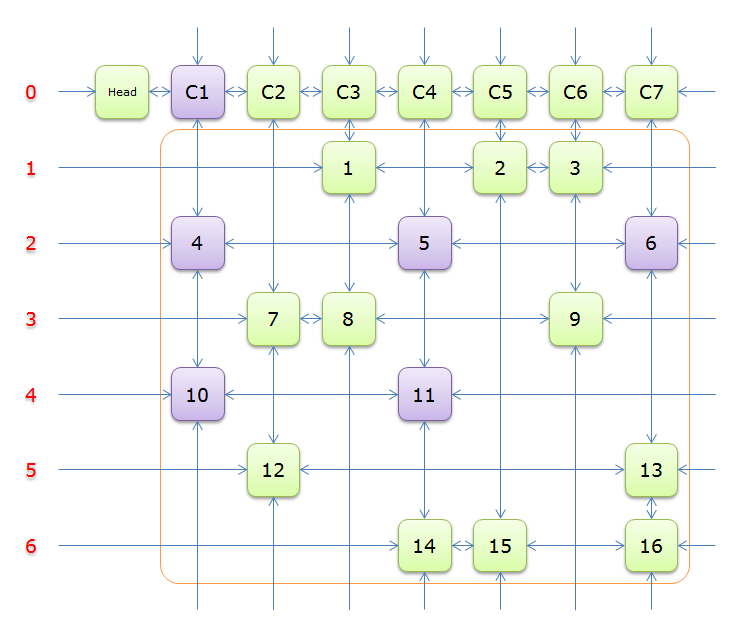
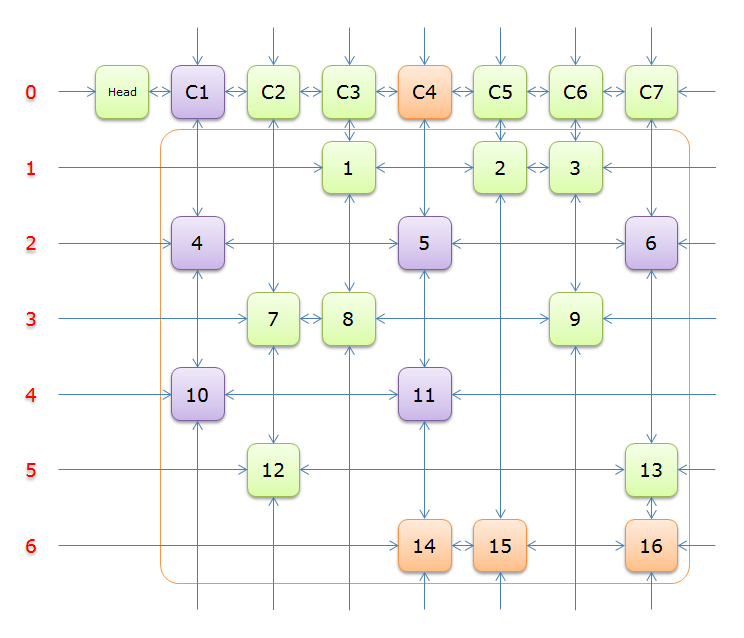
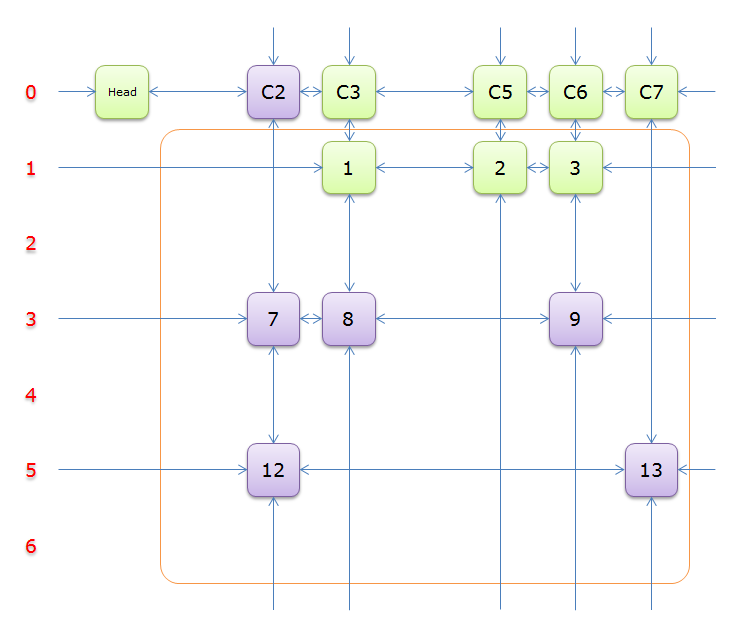
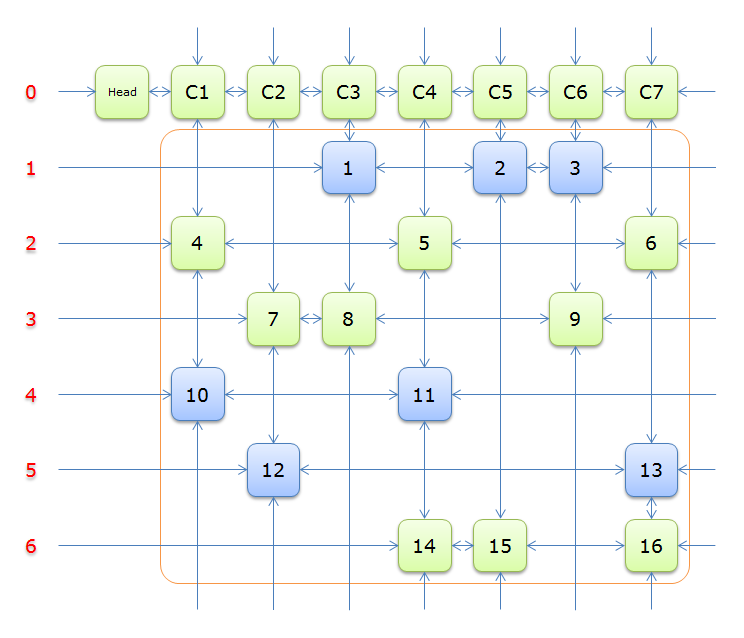
下圖就是根據題目構建好的交叉十字迴圈雙向鏈(構建的過程後面的詳述)
就上圖解釋一下
每個綠色方塊是一個元素,其中Head和C1、C2、……、C7是輔助元素。橙色框中的元素是原矩陣中1的元素,給他們標上號(從1到16)
左側的紅色,標示的是行號,輔助元素所在的行是0行,其餘元素所在的行從1到6
每兩個元素之間有一個雙向箭頭連線,表示雙向鏈中相鄰兩個元素的關係(水平的是左右關係、垂直的是上下關係)
單向的箭頭並不是表示單向關係,而因為是迴圈雙向鏈,左側的單向箭頭和右側的單向箭頭(上邊的和下邊的)組成了一個雙向箭頭,例如元素14左側的單向箭頭和元素16右側的單項箭頭組成一個雙向箭頭,表示14.Left=16、16.Right=14;同理,元素14下邊的單項箭頭和元素C4上邊的單向箭頭組成一個雙向箭頭,表示14.Down=C4、C4.Up=14
接下來,利用圖來解釋Dancing Links是如何求解精確覆蓋問題
1、首先判斷Head.Right=Head?若是,求解結束,輸出解;若不是,求解還沒結束,到步驟2(也可以判斷Head.Left=Head?)
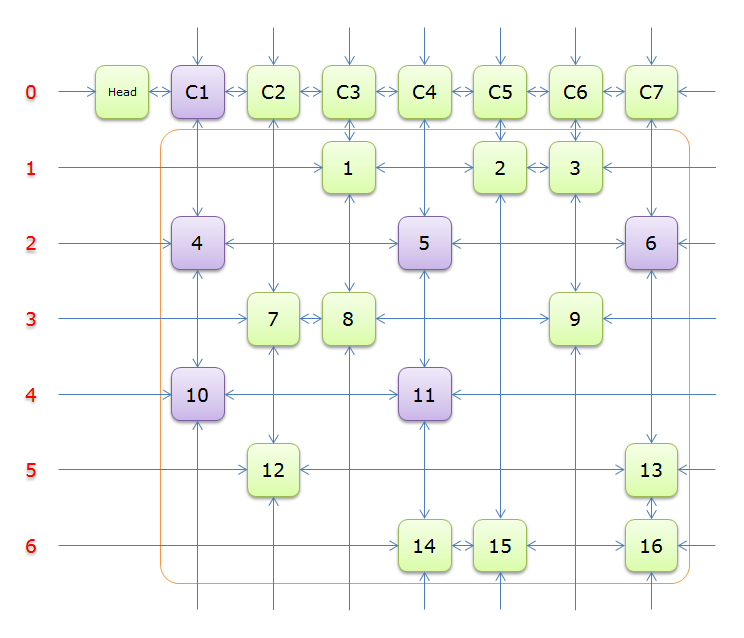
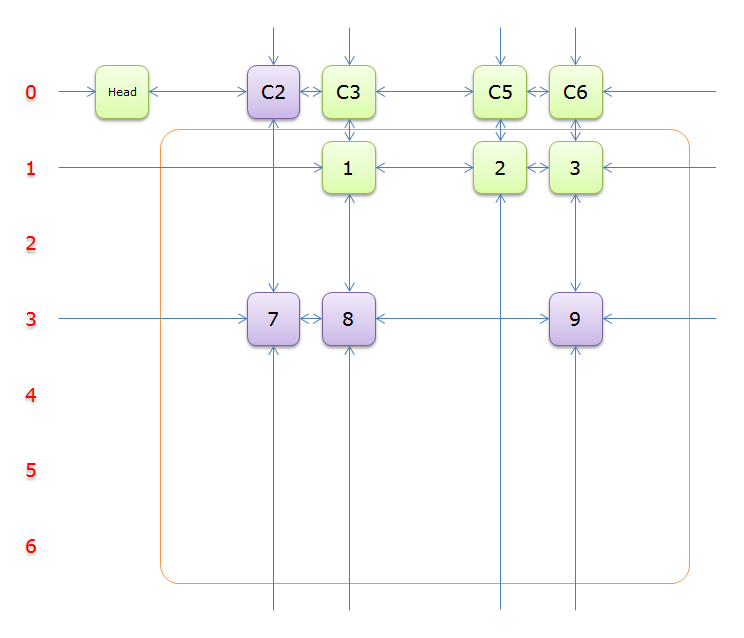
2、獲取Head.Right元素,即元素C1,並標示元素C1(標示元素C1,指的是標示C1、和C1所在列的所有元素、以及該元素所在行的元素,並從雙向鏈中移除這些元素)。如下圖中的紫色部分。
如上圖可知,行2和行4中的一個必是答案的一部分(其他行中沒有元素能覆蓋列C1),先假設選擇的是行2
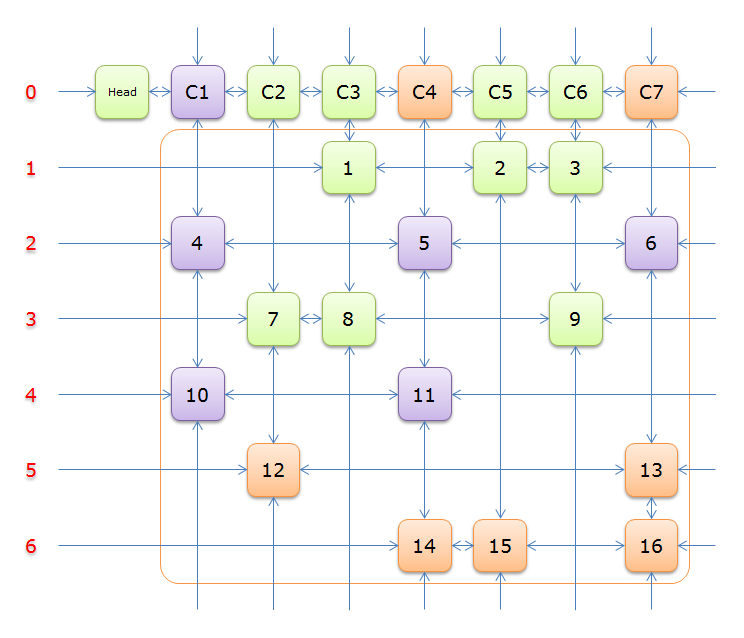
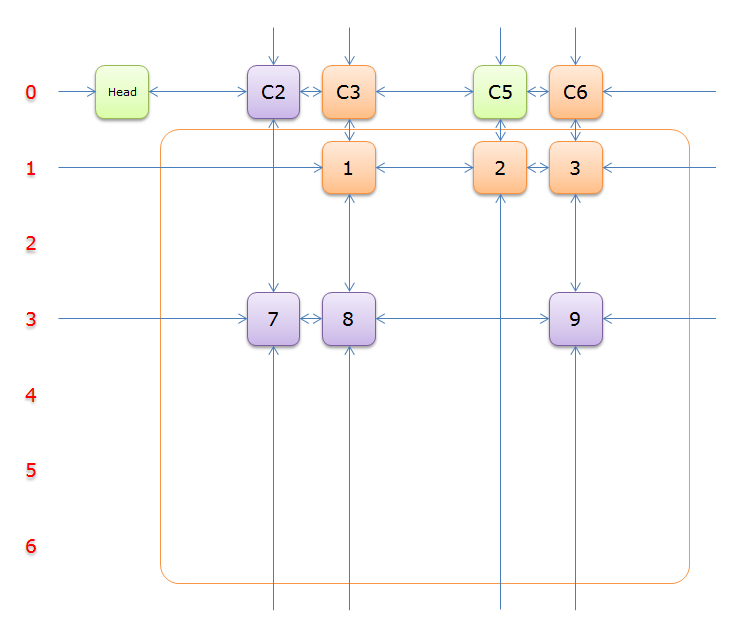
3、選擇行2(在答案棧中壓入2),標示該行中的其他元素(元素5和元素6)所在的列首元素,即標示元素C4和標示元素C7,下圖中的橙色部分。
注意的是,即使元素5在步驟2中就從雙向鏈中移除,但是元素5的Col分量還是指向元素C4的,這裡體現了雙向鏈的強大作用。
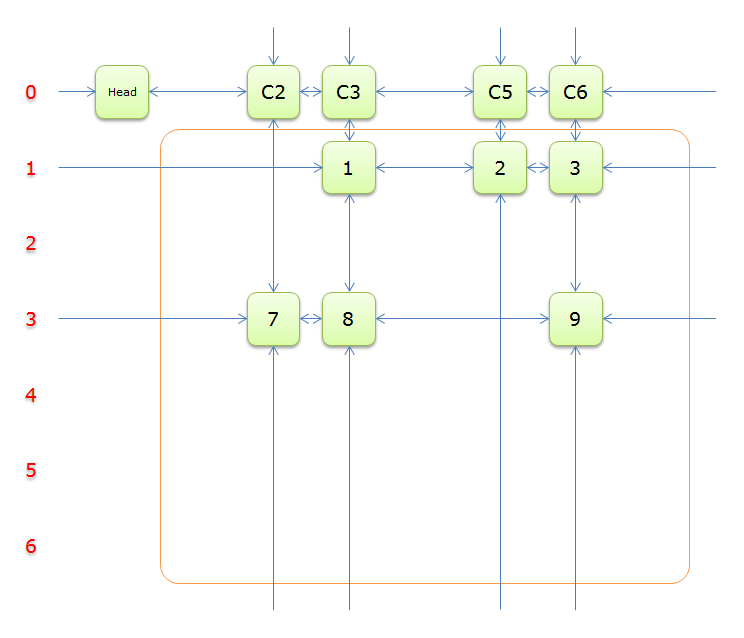
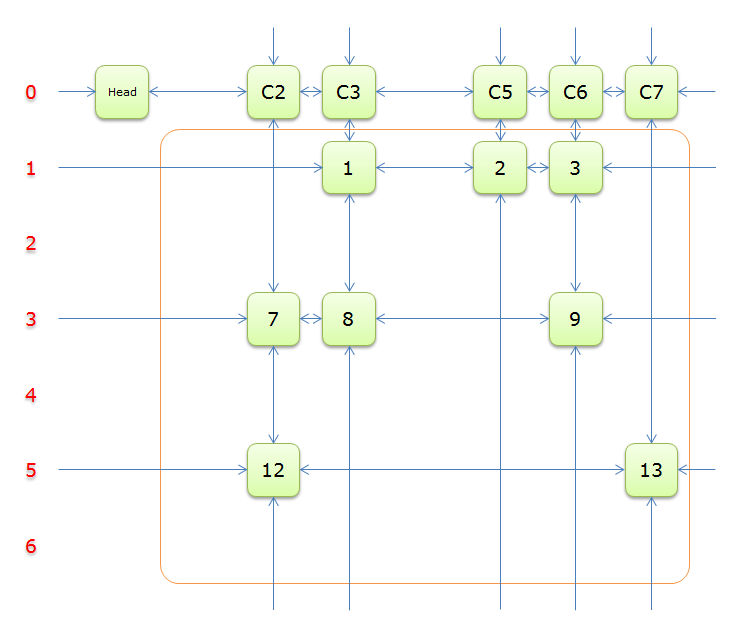
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
一下子空了好多,是不是轉換為一個少了很多元素的精確覆蓋問題?,利用遞迴的思想,很快就能寫出求解的過程來。我們繼續完成求解過程
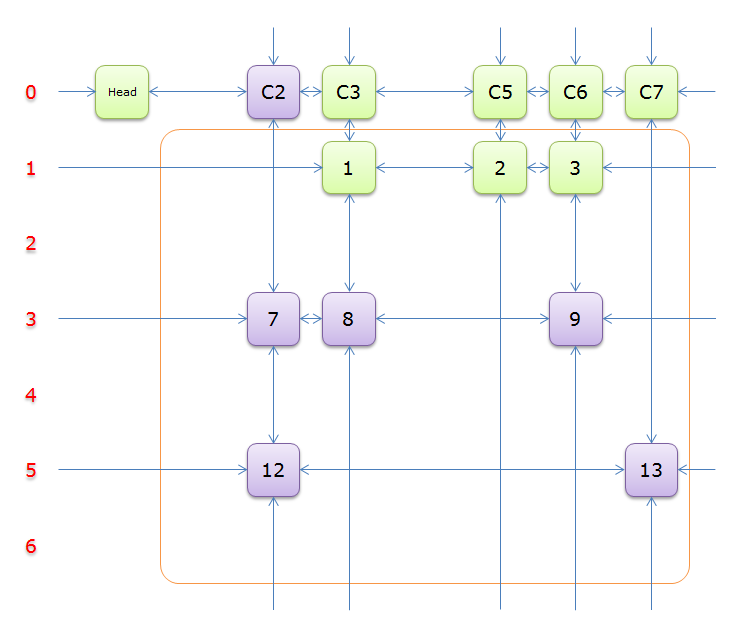
4、獲取Head.Right元素,即元素C2,並標示元素C2。如下圖中的紫色部分。
如圖,列C2只有元素7覆蓋,故答案只能選擇行3
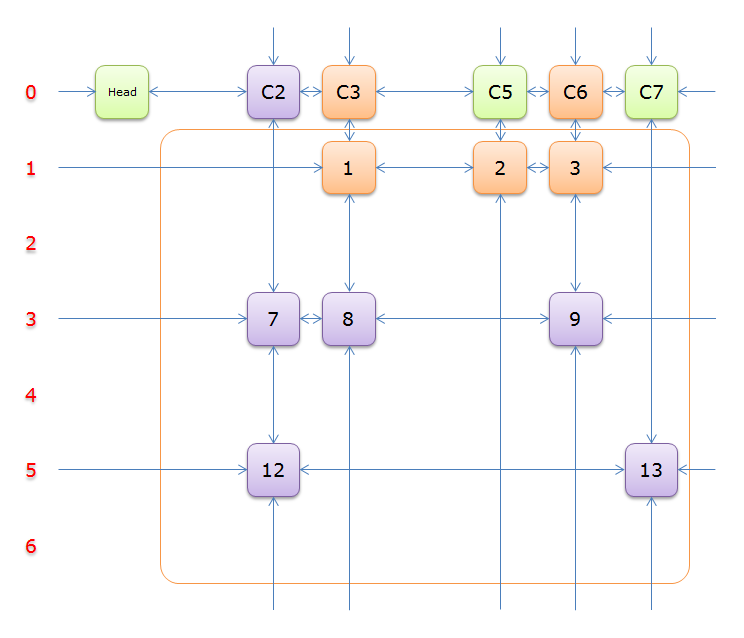
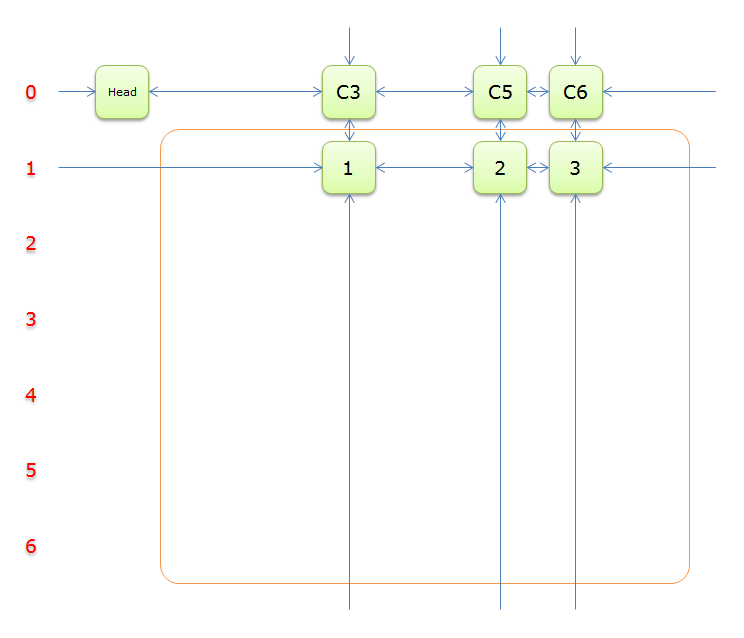
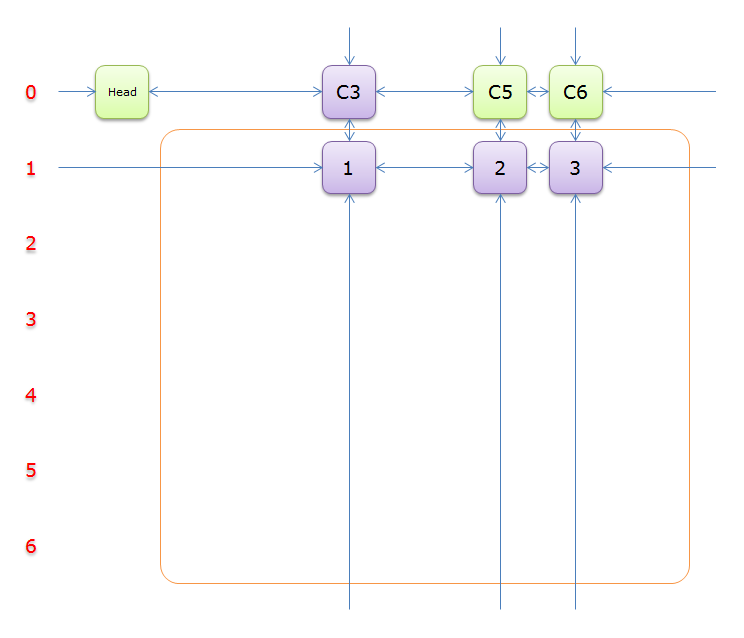
5、選擇行3(在答案棧中壓入3),標示該行中的其他元素(元素8和元素9)所在的列首元素,即標示元素C3和標示元素C6,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
6、獲取Head.Right元素,即元素C5,元素C5中的垂直雙向鏈中沒有其他元素,也就是沒有元素覆蓋列C5。說明當前求解失敗。要回溯到之前的分叉選擇步驟(步驟2)。那要回標列首元素(把列首元素、所在列的元素,以及對應行其餘的元素。並恢復這些元素到雙向鏈中),回標列首元素的順序是標示元素的順序的反過來。從前文可知,順序是回標列首C6、回標列首C3、回標列首C2、回標列首C7、回標列首C4。表面上看起來比較複雜,實際上利用遞迴,是一件很簡單的事。並把答案棧恢復到步驟2(清空的狀態)的時候。又回到下圖所示
7、由於之前選擇行2導致無解,因此這次選擇行4(再無解就整個問題就無解了)。選擇行4(在答案棧中壓入4),標示該行中的其他元素(元素11)所在的列首元素,即標示元素C4,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
8、獲取Head.Right元素,即元素C2,並標示元素C2。如下圖中的紫色部分。
如圖,行3和行5都可以選擇
9、選擇行3(在答案棧中壓入3),標示該行中的其他元素(元素8和元素9)所在的列首元素,即標示元素C3和標示元素C6,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
10、獲取Head.Right元素,即元素C5,元素C5中的垂直雙向鏈中沒有其他元素,也就是沒有元素覆蓋列C5。說明當前求解失敗。要回溯到之前的分叉選擇步驟(步驟8)。從前文可知,回標列首C6、回標列首C3。並把答案棧恢復到步驟8(答案棧中只有4)的時候。又回到下圖所示
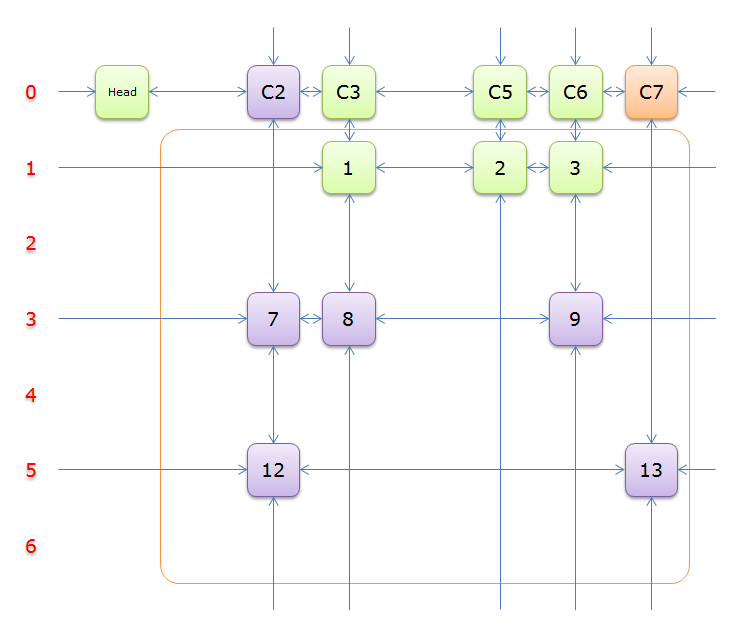
11、由於之前選擇行3導致無解,因此這次選擇行5(在答案棧中壓入5),標示該行中的其他元素(元素13)所在的列首元素,即標示元素C7,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
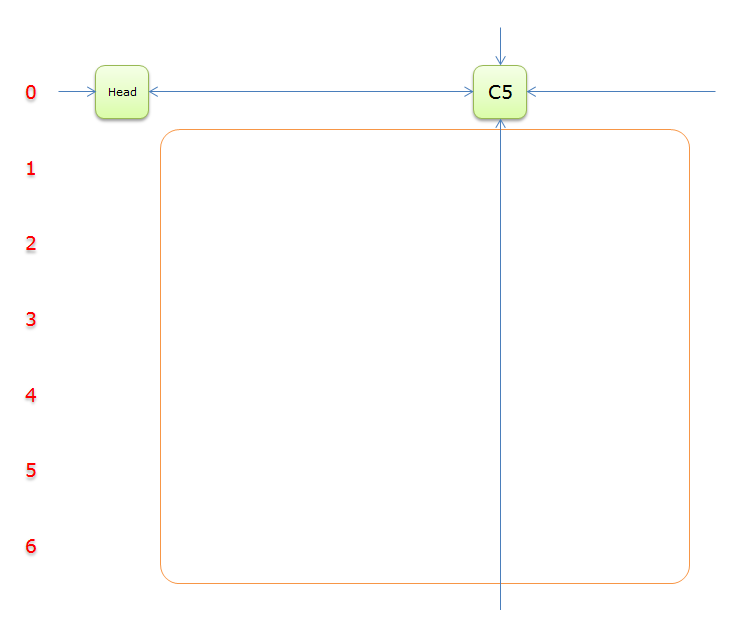
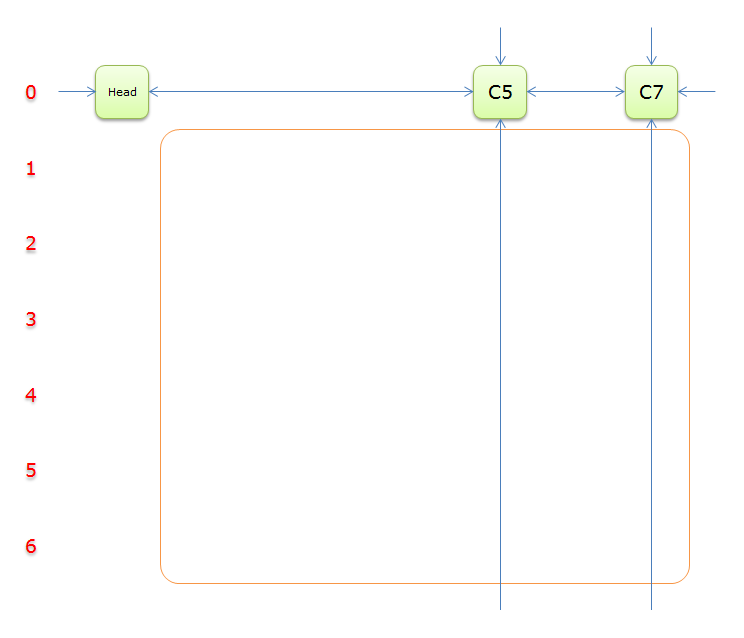
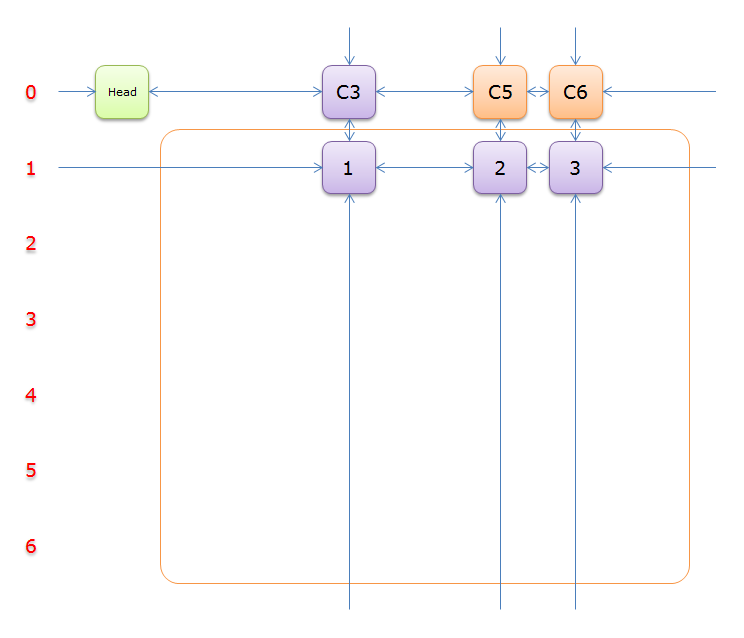
12、獲取Head.Right元素,即元素C3,並標示元素C3。如下圖中的紫色部分。
13、如上圖,列C3只有元素1覆蓋,故答案只能選擇行3(在答案棧壓入1)。標示該行中的其他元素(元素2和元素3)所在的列首元素,即標示元素C5和標示元素C6,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
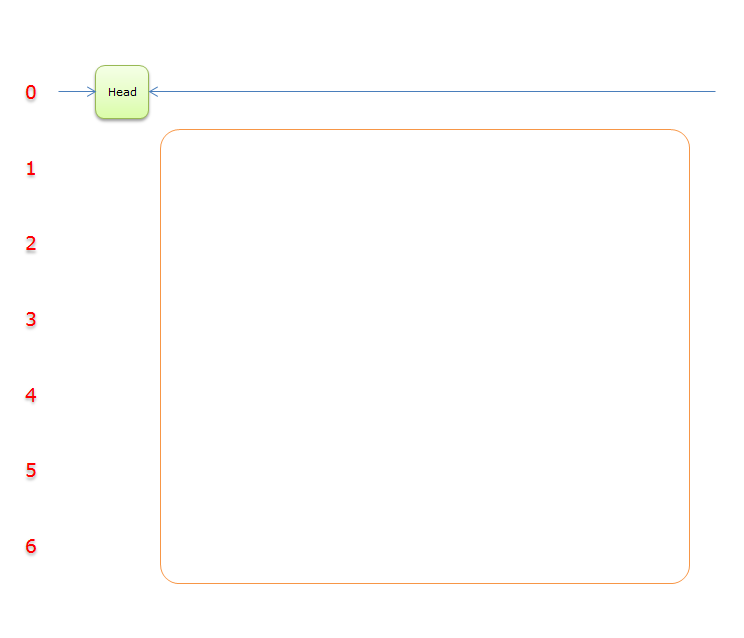
14、因為Head.Right=Head。故,整個過程求解結束。輸出答案,答案棧中的答案分別是4、5、1。表示該問題的解是第4、5、1行覆蓋所有的列。如下圖所示(藍色的部分)
從以上的14步來看,可以把Dancing Links的求解過程表述如下
1、Dancing函式的入口
2、判斷Head.Right=Head?,若是,輸出答案,返回True,退出函式。
3、獲得Head.Right的元素C
4、標示元素C
5、獲得元素C所在列的一個元素
6、標示該元素同行的其餘元素所在的列首元素
7、獲得一個簡化的問題,遞迴呼叫Daning函式,若返回的True,則返回True,退出函式。
8、若返回的是False,則回標該元素同行的其餘元素所在的列首元素,回標的順序和之前標示的順序相反
9、獲得元素C所在列的下一個元素,若有,跳轉到步驟6
10、若沒有,回標元素C,返回False,退出函式。
之前的文章的表述,為了表述簡單,採用面向物件的思路,說每個元素有6個分量,分別是Left、Right、Up、Down、Col、Row分量。
但在實際的編碼中,用陣列也能實現相同的作用。例如:用Left()表示所有元素的Left分量,Left(1)表示元素1的Left分量
在前文中,元素分為Head元素、列首元素(C1、C2等)、普通元素。在編碼中,三種元素統一成一種元素。如上題,0表示Head元素,1表示元素C1、2表示元素C2、……、7表示元素C7,從8開始表示普通元素。這是統一後,編碼的簡便性。利用陣列的下標來表示元素,宛若指標一般。

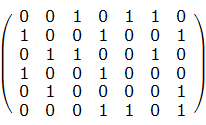
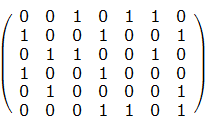
![clip_image002[4]](https://img-blog.csdnimg.cn/20181226144019550)
![clip_image002[6]](https://img-blog.csdnimg.cn/20181226144019566)
![clip_image002[8]](https://img-blog.csdnimg.cn/20181226144019580)
![clip_image002[10]](https://img-blog.csdnimg.cn/20181226144019595)