跳躍的舞者,舞蹈鏈(Dancing Links)演算法——求解精確覆蓋問題
精確覆蓋問題的定義:給定一個由0-1組成的矩陣,是否能找到一個行的集合,使得集合中每一列都恰好包含一個1
例如:如下的矩陣
就包含了這樣一個集合(第1、4、5行)
如何利用給定的矩陣求出相應的行的集合呢?我們採用回溯法
先假定選擇第1行,如下所示:
如上圖中所示,紅色的那行是選中的一行,這一行中有3個1,分別是第3、5、6列。
由於這3列已經包含了1,故,把這三列往下標示,圖中的藍色部分。藍色部分包含3個1,分別在2行中,把這2行用紫色標示出來
根據定義,同一列的1只能有1個,故紫色的兩行,和紅色的一行的1相沖突。
那麼在接下來的求解中,紅色的部分、藍色的部分、紫色的部分都不能用了,把這些部分都刪除,得到一個新的矩陣
行分別對應矩陣1中的第2、4、5行
列分別對應矩陣1中的第1、2、4、7列
於是問題就轉換為一個規模小點的精確覆蓋問題
在新的矩陣中再選擇第1行,如下圖所示
還是按照之前的步驟,進行標示。紅色、藍色和紫色的部分又全都刪除,導致新的空矩陣產生,而紅色的一行中有0(有0就說明這一列沒有1覆蓋)。說明,第1行選擇是錯誤的
那麼回到之前,選擇第2行,如下圖所示
按照之前的步驟,進行標示。把紅色、藍色、紫色部分刪除後,得到新的矩陣
行對應矩陣2中的第3行,矩陣1中的第5行
列對應矩陣2中的第2、4列,矩陣1中的第2、7列
由於剩下的矩陣只有1行,且都是1,選擇這一行,問題就解決
於是該問題的解就是矩陣1中第1行、矩陣2中的第2行、矩陣3中的第1行。也就是矩陣1中的第1、4、5行
在求解這個問題的過程中,我們第1步選擇第1行是正確的,但是不是每個題目第1步選擇都是正確的,如果選擇第1行無法求解出結果出來,那麼就要推倒之前的選擇,從選擇第2行開始,以此類推
從上面的求解過程來看,實際上求解過程可以如下表示
1、從矩陣中選擇一行
2、根據定義,標示矩陣中其他行的元素
3、刪除相關行和列的元素,得到新矩陣
4、如果新矩陣是空矩陣,並且之前的一行都是1,那麼求解結束,跳轉到6;新矩陣不是空矩陣,繼續求解,跳轉到1;新矩陣是空矩陣,之前的一行中有0,跳轉到5
5、說明之前的選擇有誤,回溯到之前的一個矩陣,跳轉到1;如果沒有矩陣可以回溯,說明該問題無解,跳轉到7
6、求解結束,把結果輸出
7、求解結束,輸出無解訊息
從如上的求解流程來看,在求解的過程中有大量的快取矩陣和回溯矩陣的過程。而如何快取矩陣以及相關的資料(保證後面的回溯能正確恢復資料),也是一個比較頭疼的問題(並不是無法解決)。以及在輸出結果的時候,如何輸出正確的結果(把每一步的選擇轉換為初始矩陣相應的行)。
於是演算法大師Donald E.Knuth(《計算機程式設計藝術》的作者)出面解決了這個方面的難題。他提出了DLX(Dancing Links X)演算法。實際上,他把上面求解的過程稱為X演算法,而他提出的舞蹈鏈(Dancing Links)實際上並不是一種演算法,而是一種資料結構。一種非常巧妙的資料結構,他的資料結構在快取和回溯的過程中效率驚人,不需要額外的空間,以及近乎線性的時間。而在整個求解過程中,指標在資料之間跳躍著,就像精巧設計的舞蹈一樣,故Donald E.Knuth把它稱為Dancing Links(中文譯名舞蹈鏈)。
Dancing Links的核心是基於雙向鏈的方便操作(移除、恢復加入)
我們用例子來說明
假設雙向鏈的三個連續的元素,A1、A2、A3,每個元素有兩個分量Left和Right,分別指向左邊和右邊的元素。由定義可知
A1.Right=A2,A2.Right=A3
A2.Left=A1,A3.Left=A2
在這個雙向鏈中,可以由任一個元素得到其他兩個元素,A1.Right.Right=A3,A3.Left.Left=A1等等
現在把A2這個元素從雙向鏈中移除(不是刪除)出去,那麼執行下面的操作就可以了
A1.Right=A3,A3.Left=A1
那麼就直接連線起A1和A3。A2從雙向鏈中移除出去了。但僅僅是從雙向鏈中移除了,A2這個實體還在,並沒有刪除。只是在雙向鏈中遍歷的話,遍歷不到A2了。
那麼A2這個實體中的兩個分量Left和Right指向誰?由於實體還在,而且沒有修改A2分量的操作,那麼A2的兩個分量指向沒有發生變化,也就是在移除前的指向。即A2.Left=A1和A2.Right=A3
如果此時發現,需要把A2這個元素重新加入到雙向鏈中的原來的位置,也就是A1和A3的中間。由於A2的兩個分量沒有發生變化,仍然指向A1和A3。那麼只要修改A1的Right分量和A3的Left就行了。也就是下面的操作
A1.Right=A2,A3.Left=A2
仔細想想,上面兩個操作(移除和恢復加入)對應了什麼?是不是對應了之前的演算法過程中的關鍵的兩步?
移除操作對應著快取資料、恢復加入操作對應著回溯資料。而美妙的是,這兩個操作不再佔用新的空間,時間上也是極快速的
在很多實際運用中,把雙向鏈的首尾相連,構成迴圈雙向鏈
Dancing Links用的資料結構是交叉十字迴圈雙向鏈
而Dancing Links中的每個元素不僅是橫向迴圈雙向鏈中的一份子,又是縱向迴圈雙向鏈的一份子。
因為精確覆蓋問題的矩陣往往是稀疏矩陣(矩陣中,0的個數多於1),Dancing Links僅僅記錄矩陣中值是1的元素。
Dancing Links中的每個元素有6個分量
分別:Left指向左邊的元素、Right指向右邊的元素、Up指向上邊的元素、Down指向下邊的元素、Col指向列標元素、Row指示當前元素所在的行
Dancing Links還要準備一些輔助元素(為什麼需要這些輔助元素?沒有太多的道理,大師認為這能解決問題,實際上是解決了問題)
Ans():Ans陣列,在求解的過程中保留當前的答案,以供最後輸出答案用。
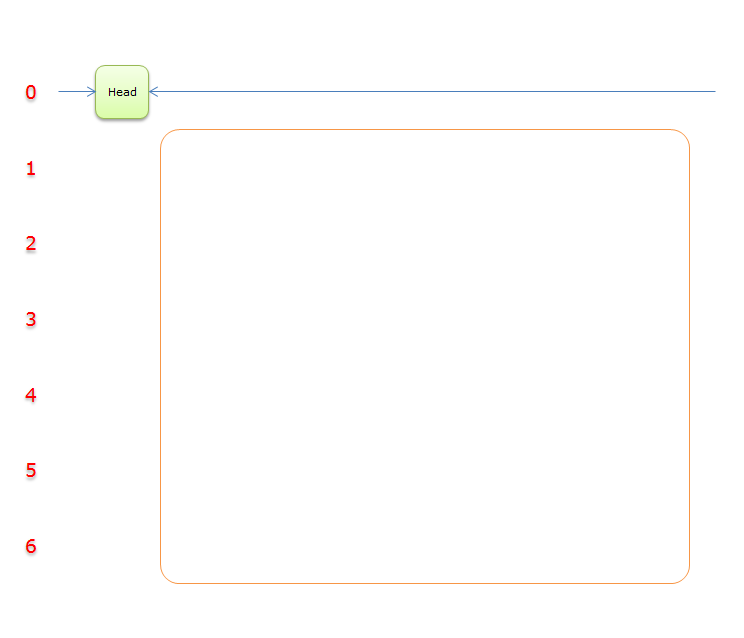
Head元素:求解的輔助元素,在求解的過程中,當判斷出Head.Right=Head(也可以是Head.Left=Head)時,求解結束,輸出答案。Head元素只有兩個分量有用。其餘的分量對求解沒啥用
C元素:輔助元素,稱列標元素,每列有一個列標元素。本文開始的題目的列標元素分別是C1、C2、C3、C4、C5、C6、C7。每一列的元素的Col分量都指向所在列的列標元素。列標元素的Col分量指向自己(也可以是沒有)。在初始化的狀態下,Head.Right=C1、C1.Right=C2、……、C7.Right=Head、Head.Left=C7等等。列標元素的分量Row=0,表示是處在第0行。
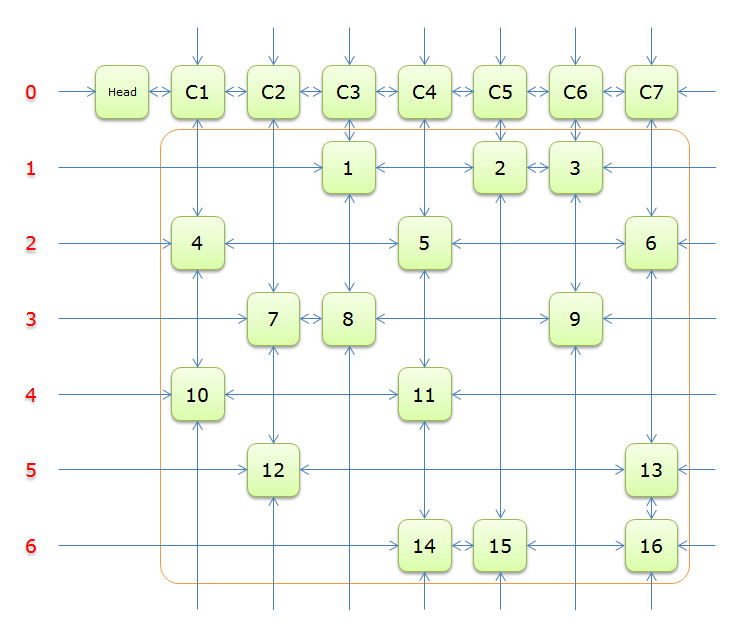
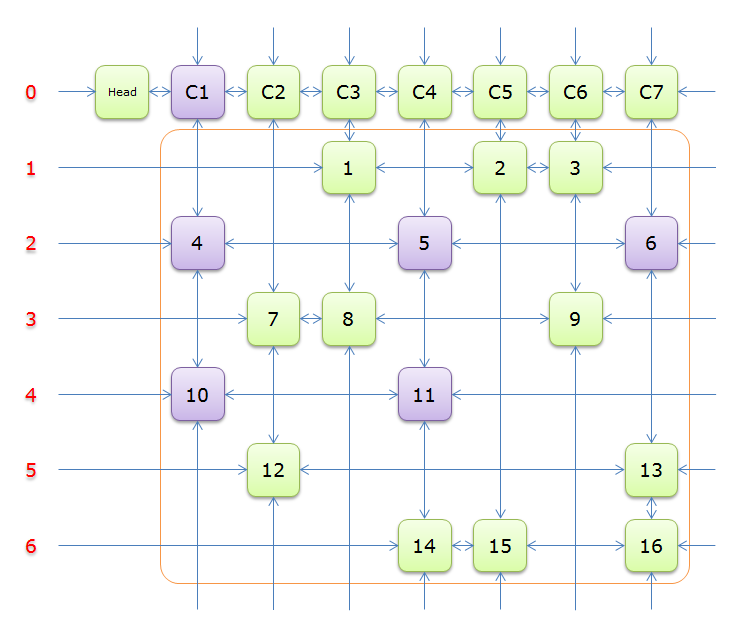
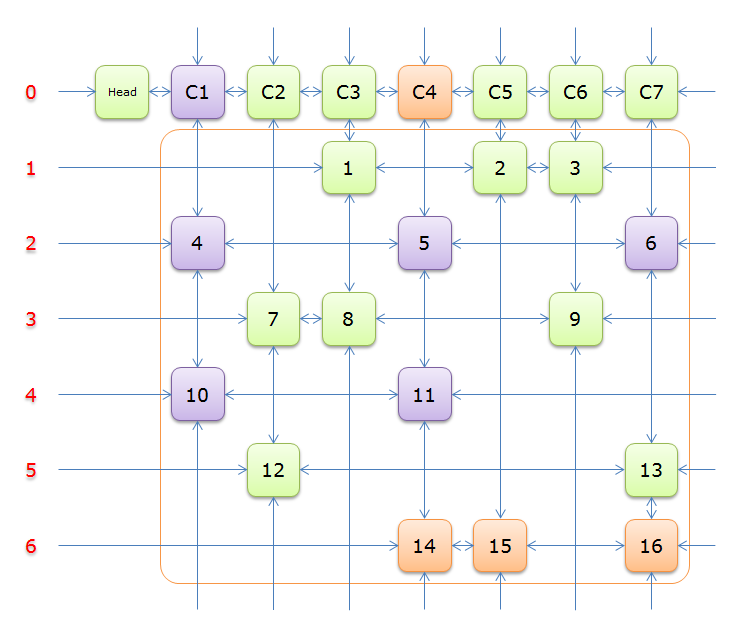
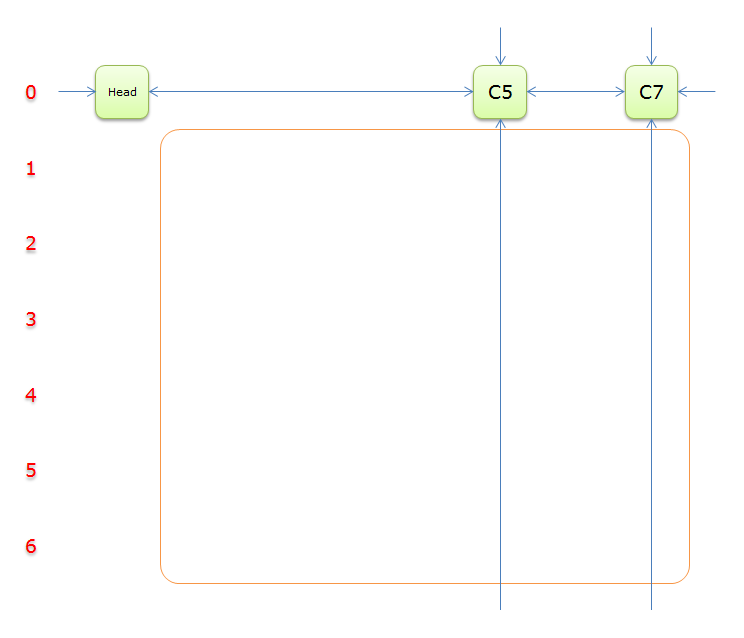
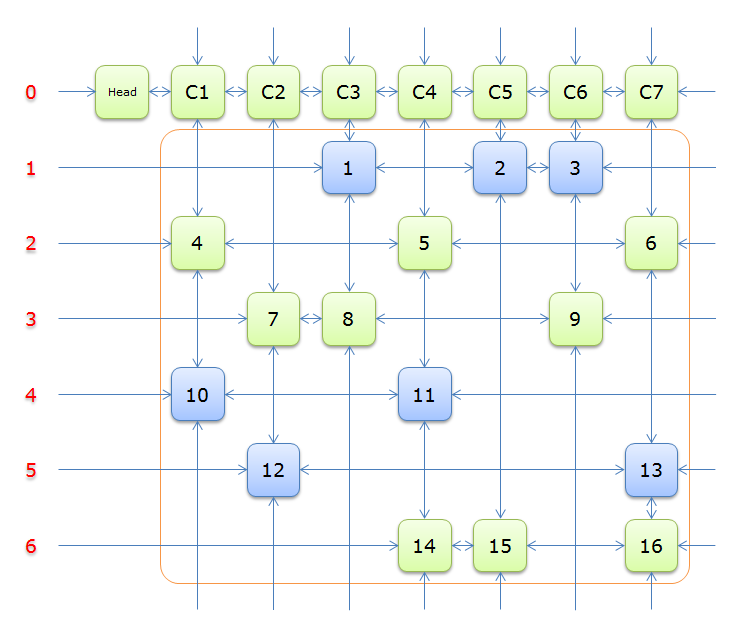
下圖就是根據題目構建好的交叉十字迴圈雙向鏈(構建的過程後面的詳述)
就上圖解釋一下
每個綠色方塊是一個元素,其中Head和C1、C2、……、C7是輔助元素。橙色框中的元素是原矩陣中1的元素,給他們標上號(從1到16)
左側的紅色,標示的是行號,輔助元素所在的行是0行,其餘元素所在的行從1到6
每兩個元素之間有一個雙向箭頭連線,表示雙向鏈中相鄰兩個元素的關係(水平的是左右關係、垂直的是上下關係)
單向的箭頭並不是表示單向關係,而因為是迴圈雙向鏈,左側的單向箭頭和右側的單向箭頭(上邊的和下邊的)組成了一個雙向箭頭,例如元素14左側的單向箭頭和元素16右側的單項箭頭組成一個雙向箭頭,表示14.Left=16、16.Right=14;同理,元素14下邊的單項箭頭和元素C4上邊的單向箭頭組成一個雙向箭頭,表示14.Down=C4、C4.Up=14
接下來,利用圖來解釋Dancing Links是如何求解精確覆蓋問題
1、首先判斷Head.Right=Head?若是,求解結束,輸出解;若不是,求解還沒結束,到步驟2(也可以判斷Head.Left=Head?)
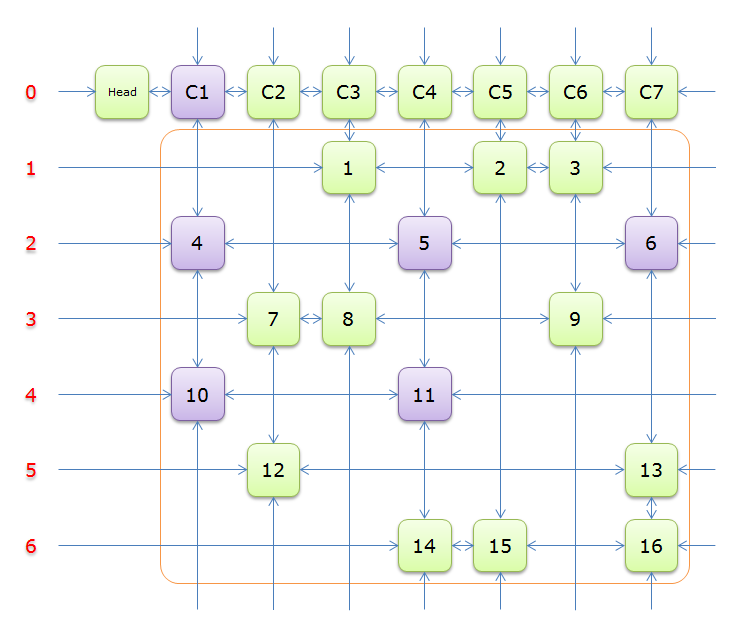
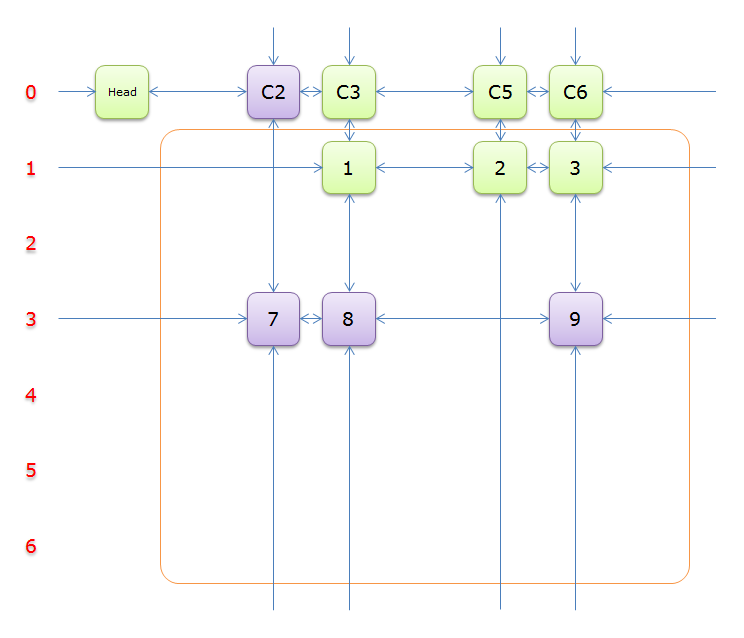
2、獲取Head.Right元素,即元素C1,並標示元素C1(標示元素C1,指的是標示C1、和C1所在列的所有元素、以及該元素所在行的元素,並從雙向鏈中移除這些元素)。如下圖中的紫色部分。
如上圖可知,行2和行4中的一個必是答案的一部分(其他行中沒有元素能覆蓋列C1),先假設選擇的是行2
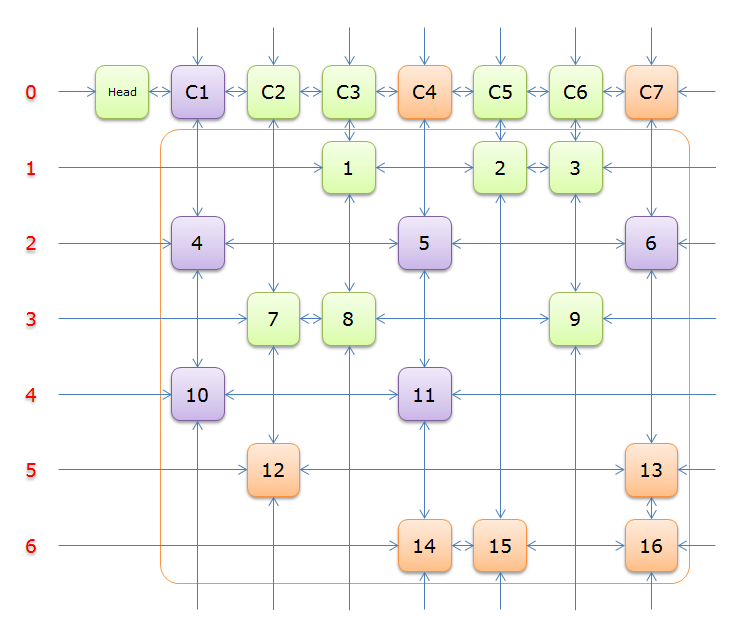
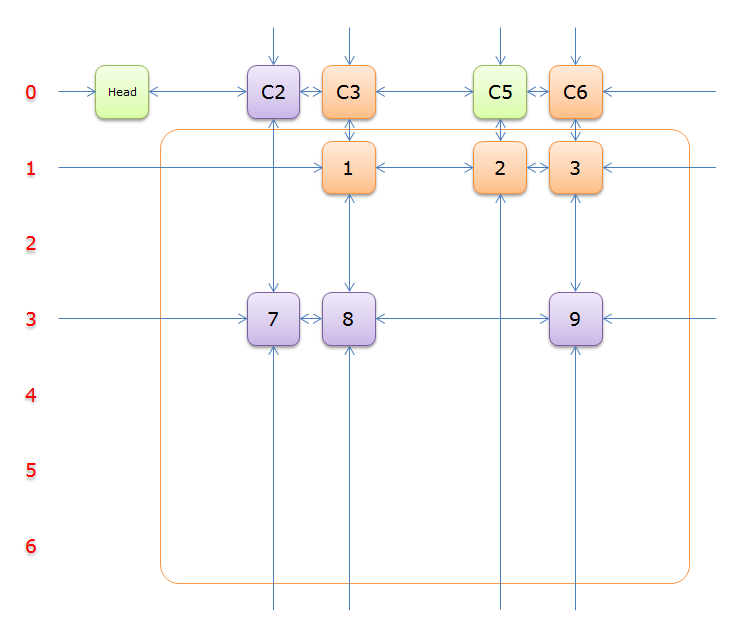
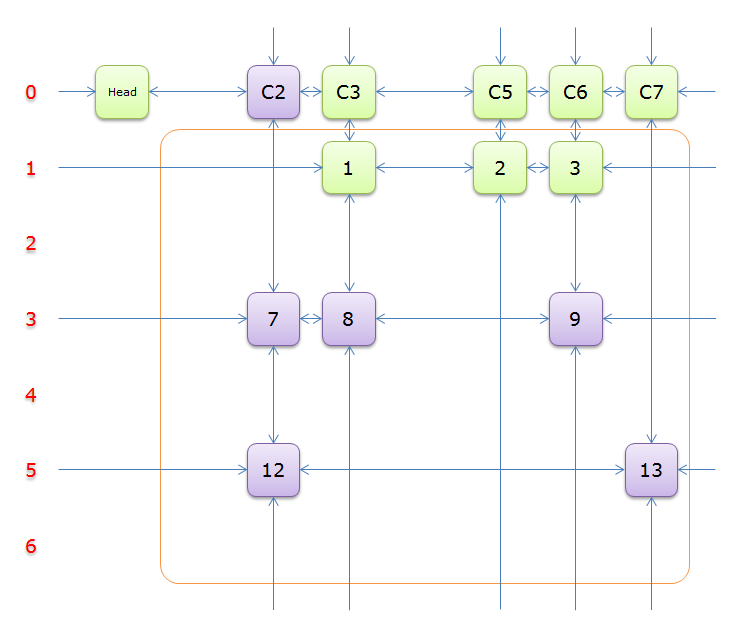
3、選擇行2(在答案棧中壓入2),標示該行中的其他元素(元素5和元素6)所在的列首元素,即標示元素C4和標示元素C7,下圖中的橙色部分。
注意的是,即使元素5在步驟2中就從雙向鏈中移除,但是元素5的Col分量還是指向元素C4的,這裡體現了雙向鏈的強大作用。
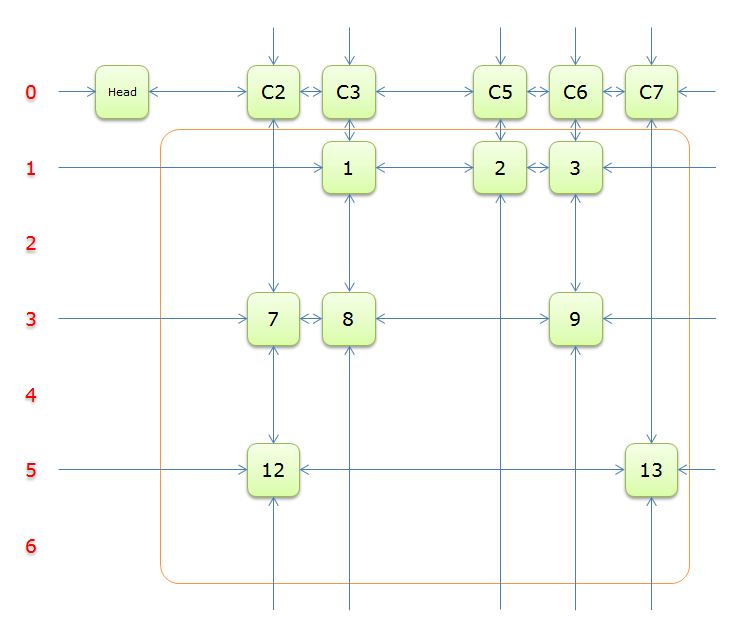
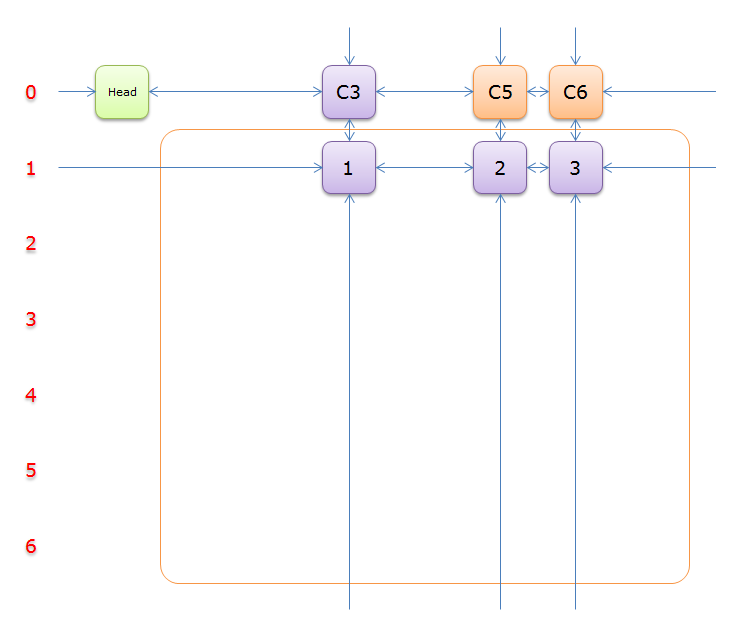
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
一下子空了好多,是不是轉換為一個少了很多元素的精確覆蓋問題?,利用遞迴的思想,很快就能寫出求解的過程來。我們繼續完成求解過程
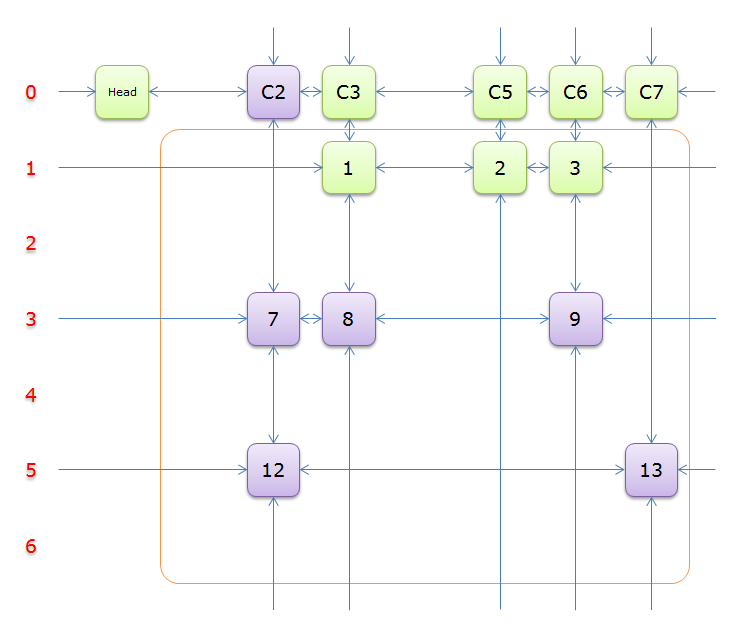
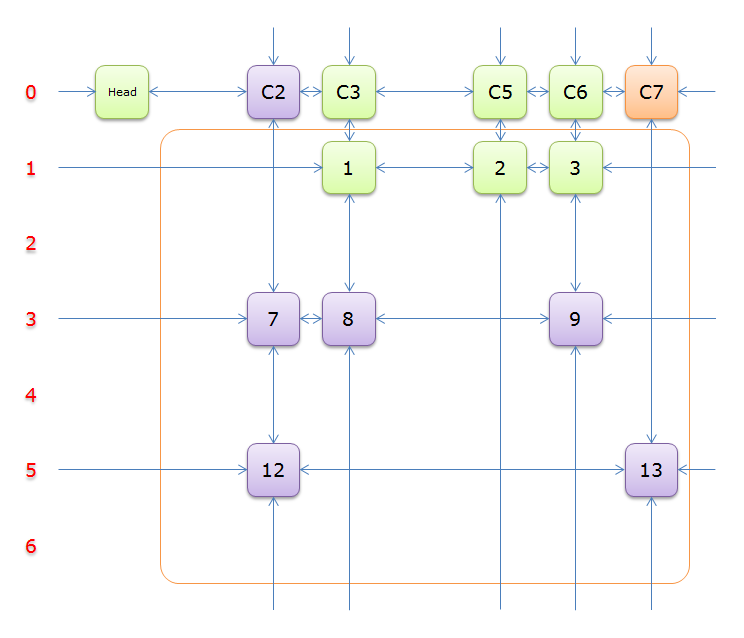
4、獲取Head.Right元素,即元素C2,並標示元素C2。如下圖中的紫色部分。
如圖,列C2只有元素7覆蓋,故答案只能選擇行3
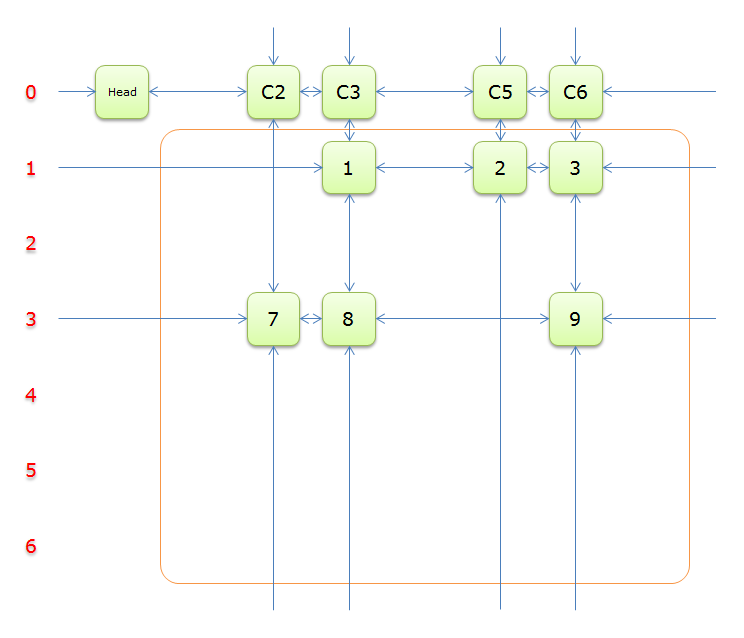
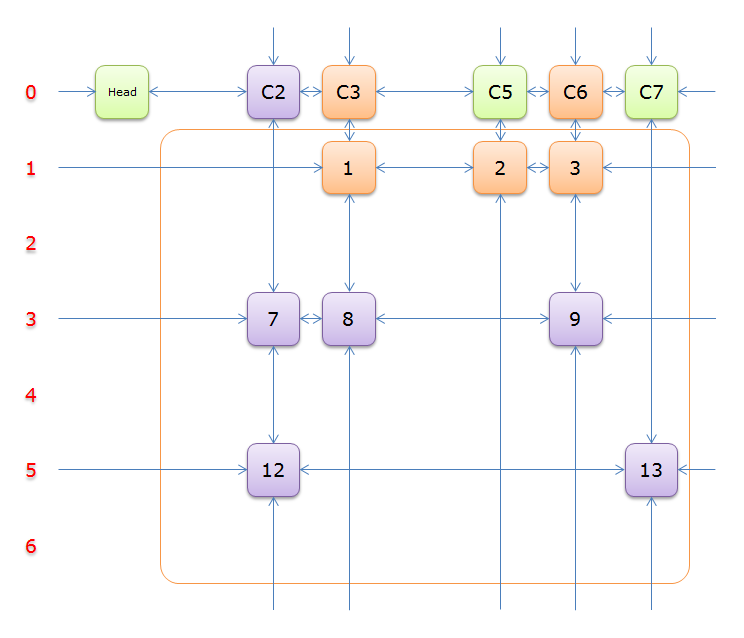
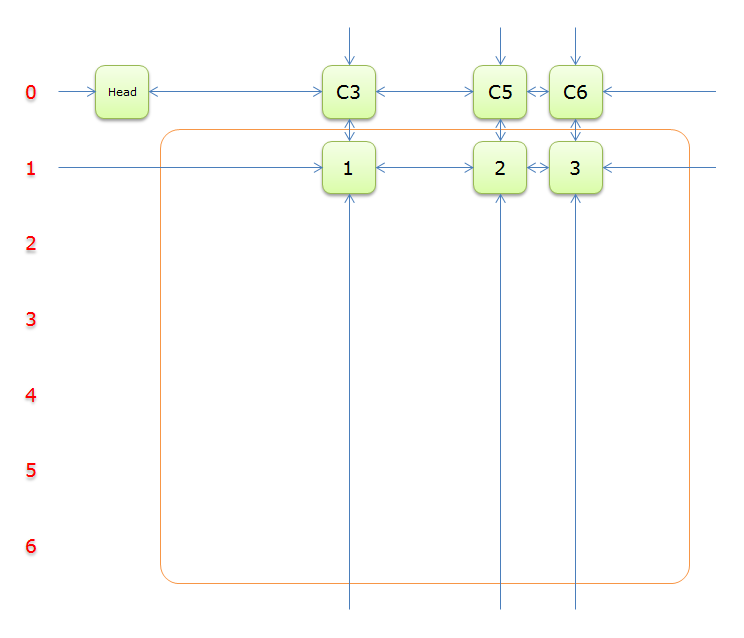
5、選擇行3(在答案棧中壓入3),標示該行中的其他元素(元素8和元素9)所在的列首元素,即標示元素C3和標示元素C6,下圖中的橙色部分。
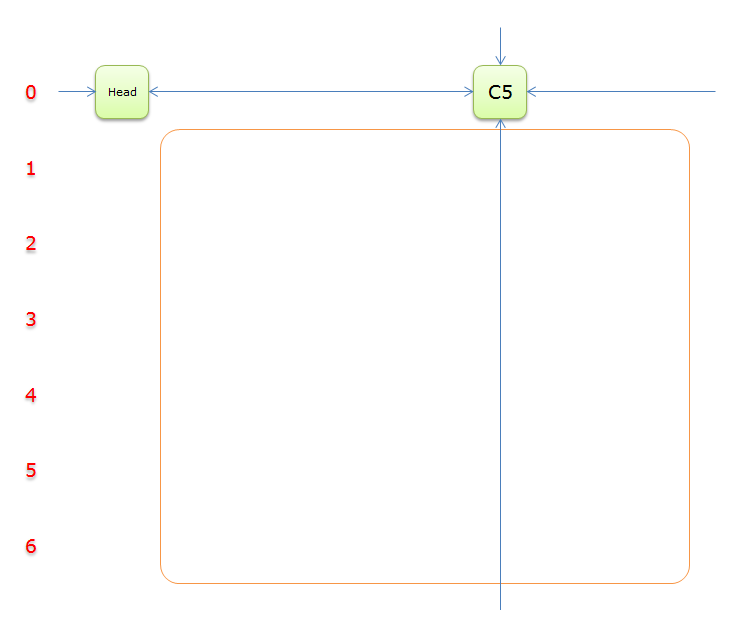
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
6、獲取Head.Right元素,即元素C5,元素C5中的垂直雙向鏈中沒有其他元素,也就是沒有元素覆蓋列C5。說明當前求解失敗。要回溯到之前的分叉選擇步驟(步驟2)。那要回標列首元素(把列首元素、所在列的元素,以及對應行其餘的元素。並恢復這些元素到雙向鏈中),回標列首元素的順序是標示元素的順序的反過來。從前文可知,順序是回標列首C6、回標列首C3、回標列首C2、回標列首C7、回標列首C4。表面上看起來比較複雜,實際上利用遞迴,是一件很簡單的事。並把答案棧恢復到步驟2(清空的狀態)的時候。又回到下圖所示
7、由於之前選擇行2導致無解,因此這次選擇行4(再無解就整個問題就無解了)。選擇行4(在答案棧中壓入4),標示該行中的其他元素(元素11)所在的列首元素,即標示元素C4,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
8、獲取Head.Right元素,即元素C2,並標示元素C2。如下圖中的紫色部分。
如圖,行3和行5都可以選擇
9、選擇行3(在答案棧中壓入3),標示該行中的其他元素(元素8和元素9)所在的列首元素,即標示元素C3和標示元素C6,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
10、獲取Head.Right元素,即元素C5,元素C5中的垂直雙向鏈中沒有其他元素,也就是沒有元素覆蓋列C5。說明當前求解失敗。要回溯到之前的分叉選擇步驟(步驟8)。從前文可知,回標列首C6、回標列首C3。並把答案棧恢復到步驟8(答案棧中只有4)的時候。又回到下圖所示
11、由於之前選擇行3導致無解,因此這次選擇行5(在答案棧中壓入5),標示該行中的其他元素(元素13)所在的列首元素,即標示元素C7,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
12、獲取Head.Right元素,即元素C3,並標示元素C3。如下圖中的紫色部分。
13、如上圖,列C3只有元素1覆蓋,故答案只能選擇行3(在答案棧壓入1)。標示該行中的其他元素(元素2和元素3)所在的列首元素,即標示元素C5和標示元素C6,下圖中的橙色部分。
把上圖中的紫色部分和橙色部分移除的話,剩下的綠色部分就如下圖所示
14、因為Head.Right=Head。故,整個過程求解結束。輸出答案,答案棧中的答案分別是4、5、1。表示該問題的解是第4、5、1行覆蓋所有的列。如下圖所示(藍色的部分)
從以上的14步來看,可以把Dancing Links的求解過程表述如下
1、Dancing函式的入口
2、判斷Head.Right=Head?,若是,輸出答案,返回True,退出函式。
3、獲得Head.Right的元素C
4、標示元素C
5、獲得元素C所在列的一個元素
6、標示該元素同行的其餘元素所在的列首元素
7、獲得一個簡化的問題,遞迴呼叫Daning函式,若返回的True,則返回True,退出函式。
8、若返回的是False,則回標該元素同行的其餘元素所在的列首元素,回標的順序和之前標示的順序相反
9、獲得元素C所在列的下一個元素,若有,跳轉到步驟6
10、若沒有,回標元素C,返回False,退出函式。
之前的文章的表述,為了表述簡單,採用面向物件的思路,說每個元素有6個分量,分別是Left、Right、Up、Down、Col、Row分量。
但在實際的編碼中,用陣列也能實現相同的作用。例如:用Left()表示所有元素的Left分量,Left(1)表示元素1的Left分量
在前文中,元素分為Head元素、列首元素(C1、C2等)、普通元素。在編碼中,三種元素統一成一種元素。如上題,0表示Head元素,1表示元素C1、2表示元素C2、……、7表示元素C7,從8開始表示普通元素。這是統一後,編碼的簡便性。利用陣列的下標來表示元素,宛若指標一般。
下面是程式碼的講解
1、該類的一些變數
Private Left() As Integer, Right() As Integer, Up() As Integer, Down() As Integer
Private Row() As Integer, Col() As Integer
Private _Head As Integer
Private _Rows As Integer, _Cols As Integer, _NodeCount As Integer
Private Ans() As Integer
前兩行表示每個元素的六個分量,用陣列表示;_Head表示元素Head,在類中初始化時令其等於0;_Rows表示矩陣的行數,_Cols表示矩陣的列數,_NodeCount表示元素的個數;Ans()用於存放答案
2、求解的主函式,Dance函式,是個遞迴函式,引數K表示當前的呼叫層數。
Public Function Dance() As Integer()
Return IIf(Dance(0) = True, Ans, Nothing)
End Function
Private Function Dance(ByVal K As Integer) As Boolean
Dim C1 As Integer = Right(_Head)
If (C1 = _Head) Then
ReDim Preserve Ans(K - 1)
Return True
End If
RemoveCol(C1)
Dim I As Integer, J As Integer
I = Down(C1)
Do While I <> C1
Ans(K) = Row(I)
J = Right(I)
Do While J <> I
RemoveCol(Col(J))
J = Right(J)
Loop
If Dance(K + 1) Then Return True
J = Left(I)
Do While J <> I
ResumeCol(Col(J))
J = Left(J)
Loop
I = Down(I)
Loop
ResumeCol(C1)
Return False
End Function
其中第一個函式Dance是對外開放的函式,它通過呼叫Dance(0)來求解問題,根據返回值來決定返回答案(當為True的時候)還是返回空(當為False的時候)
第二個函式是求解的主函式。首先通過Right(_Head)獲得_Head元素的右元素。判斷是否等於自身,若是,求解結束,因為答案儲存在Ans(0)到Ans(K-1)中,所以先把答案陣列中多餘的部分去除(利用Redim語句)。
RemoveCol函式是用來標示列首元素的,ResumeCol函式用來回標列首元素的,其中通過Col(J)獲得J元素的列首元素。在函式中有個很聰明的設計,在標示列首元素時,順序是從I元素的右側元素開始;而在回標列首元素時,順序是從I元素的左側元素開始,正好順序和標示列首元素的順序相反。
在呼叫Dance(K+1)前,把當前選中的行儲存到Ans(K)中,當Dance(K+1)返回True時,說明遞迴呼叫獲得正確的解,那直接返回True;返回False時,說明當前選擇的行不正確,回標列首元素,獲得下一個元素。
當元素C1中所在的列的其餘元素所選定的行沒有求解正確的遞迴函式時(包括C1列沒有其餘的元素),說明當前的求解失敗,回標列首元素C1,返回False
3、求解的輔助函式,RemoveCol函式,標示列首函式
Public Sub RemoveCol(ByVal Col As Integer)
Left(Right(Col)) = Left(Col)
Right(Left(Col)) = Right(Col)
Dim I As Integer, J As Integer
I = Down(Col)
Do While I <> Col
J = Right(I)
Do While J <> I
Up(Down(J)) = Up(J)
Down(Up(J)) = Down(J)
J = Right(J)
Loop
I = Down(I)
Loop
End Sub
首先,利用Left(Right(Col)) = Left(Col) 和Right(Left(Col)) = Right(Col) 把列首元素Col從水平雙向鏈中移除出去。再依次把Col所在的列的其餘元素的所在行的其餘元素從垂直雙向鏈中移除出去,利用的是Up(Down(J)) = Up(J) 和Down(Up(J)) = Down(J)。找尋Col所在列的其餘元素的順序是從下邊(Down分量)開始,移除所在行其餘元素的順序是從右邊(Right分量)開始 。可以參考之前的圖中的紫色部分。
4、求解的輔助函式,ResumeCol函式,回標列首函式
Public Sub ResumeCol(ByVal Col As Integer)
Left(Right(Col)) = Col
Right(Left(Col)) = Col
Dim I As Integer, J As Integer
I = Up(Col)
Do While (I <> Col)
J = Right(I)
Do While J <> I
Up(Down(J)) = J
Down(Up(J)) = J
J = Right(J)
Loop
I = Up(I)
Loop
End Sub
首先,利用Left(Right(Col)) = Col 和Right(Left(Col)) = Col 把列首元素Col恢復到水平雙向鏈中。再依次把Col所在的列的其餘元素的所在行的其餘元素恢復到垂直雙向鏈中,利用的是Up(Down(J)) = J 和Down(Up(J)) = J。找尋Col所在列的其餘元素的順序是從上邊(Up分量)開始(和之前的RemoveCol函式相反),恢復所在行其餘元素的順序是從右邊(Right分量)開始 。
5、類的初始化函式
Public Sub New(ByVal Cols As Integer)
ReDim Left(Cols), Right(Cols), Up(Cols), Down(Cols), Row(Cols), Col(Cols), Ans(Cols)
Dim I As Integer
Up(0) = 0
Down(0) = 0
Right(0) = 1
Left(0) = Cols
For I = 1 To Cols
Up(I) = I
Down(I) = I
Left(I) = I - 1
Right(I) = I + 1
Col(I) = I
Row(I) = 0
Next
Right(Cols) = 0
_Rows = 0
_Cols = Cols
_NodeCount = Cols
_Head = 0
End Sub
初始化函式有一個引數Cols,表示這個矩陣的列數。
初始化的時候,由於沒有傳入矩陣元素的資訊。因此,在該函式中先把輔助元素完成
0表示Head元素,1-Cols表示Cols個列的列首元素
第一句,重定義六個分量的陣列,表示Head元素和列首元素的六個分量。
Right(0) = 1表示Head元素的Right分量指向列首元素1(第1列的列首元素);Left(0) = Cols表示Head元素的Left分量指向列首元素Cols(第Cols列的列首元素)
後面的一段迴圈,給每個列首元素指定六個分量。Up和Down分量指向自己,Left分量指向左邊的列首元素(I-1),Right分量指向右邊的列首元素(I+1),Col分量指向自己,Row分量為0,參看前面的圖。最後Right(Cols)=0,Cols列的列首元素的Right分量指向Head元素
其後是一些變數的賦值。把_Head賦值為0,表示0為Head元素,是為了後面的程式碼的直觀性
6、新增矩陣元素的函式
Public Sub AppendLine(ByVal ParamArray Value() As Integer)
_Rows += 1
If Value.Length = 0 Then Exit Sub
Dim I As Integer, K As Integer = 0
For I = 0 To Value.Length - 1
If Value(I) = 1 Then
_NodeCount += 1
ReDim Preserve Left(_NodeCount)
ReDim Preserve Right(_NodeCount)
ReDim Preserve Up(_NodeCount)
ReDim Preserve Down(_NodeCount)
ReDim Preserve Row(_NodeCount)
ReDim Preserve Col(_NodeCount)
ReDim Preserve Ans(_NodeCount)
If K = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
K = 1
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = I + 1
Up(_NodeCount) = Up(I + 1)
Down(Up(I + 1)) = _NodeCount
Up(I + 1) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = I + 1
End If
Next
End Sub
把矩陣的一行元素(包括0和1)新增到類中
在前文中介紹了Dancing Links中只儲存1的元素(稀疏矩陣),因此,在新增的時候,先判斷值是否是1。
那實際上問題是如何把元素新增到雙向鏈中,在新增的過程中,自左向右新增。
先考量如何把元素新增到水平雙向鏈中
當新增這一行的第一個元素時,由於還沒有雙向鏈,首先構造一個只有一個元素的雙向鏈。Left(_NodeCount) = _NodeCount和Right(_NodeCount) = _NodeCount。這個元素的Left和Right分量都指向自己。
從第二個元素開始。問題就轉換為把元素新增到水平雙向鏈的末尾,實際上需要知道之前的水平雙向鏈的最左邊的元素和最右邊的元素,可以肯定的是最右邊的元素是_NodeCount-1,最左邊的元素是什麼?之前並沒有快取啊。由於是迴圈雙向鏈,Right(_NodeCount-1)就是這雙向鏈的最左邊的元素。Left(_NodeCount) = _NodeCount - 1,把當前元素的Left分量指向最右邊的元素即_NodeCount-1;Right(_NodeCount) = Right(_NodeCount - 1) ,把當前元素的Right分量指向最左邊的元素即Right(_NodeCount-1);Left(Right(_NodeCount - 1)) = _NodeCount,把最左邊的元素即Right(_NodeCount-1)的Left分量指向當前元素;Right(_NodeCount - 1) = _NodeCount,把最右邊的元素即_NodeCount-1的Right分量指向當前元素
再考量如何把元素新增到垂直雙向鏈
同樣,問題就轉換為把元素新增到垂直雙向鏈的末尾,實際上需要知道之前的垂直雙向鏈的最上邊的元素和最下邊的元素。和水平雙向鏈的不同,我們沒法知道最下邊的元素,但是我們可以利用列首元素知道最上邊的元素(列首元素就是該雙向鏈中最上邊的元素)。因此,最上邊的元素是I+1(因為I是從0開始的,故相應的列就是I+1,相應的列首元素就是I+1),那麼最下邊的元素就是Up(I+1)。Down(_NodeCount) = I + 1,把當前元素的Down分量指向最上邊的元素即I+1;Up(_NodeCount) = Up(I + 1) ,把當前元素的Up分量指向最下邊的元素即Up(I+1);Down(Up(I + 1)) = _NodeCount,把最下邊元素即Up(I+1)的Down分量指向當前元素;Up(I + 1) = _NodeCount,把最上邊元素即I+1的Up分量指向當前元素
至此,完成了把當前元素新增到兩個雙向鏈的過程
最後,給當前元素的Row分量和Col分量賦值
在文首的題目中,新增第一行的資料,如下呼叫
AppendLine(0,0,1,0,1,1,0)
如果一行中有大量的0,那麼用下面的函式比較方便
Public Sub AppendLineByIndex(ByVal ParamArray Index() As Integer)
_Rows += 1
If Index.Length = 0 Then Exit Sub
Dim I As Integer, K As Integer = 0
ReDim Preserve Left(_NodeCount + Index.Length)
ReDim Preserve Right(_NodeCount + Index.Length)
ReDim Preserve Up(_NodeCount + Index.Length)
ReDim Preserve Down(_NodeCount + Index.Length)
ReDim Preserve Row(_NodeCount + Index.Length)
ReDim Preserve Col(_NodeCount + Index.Length)
ReDim Preserve Ans(_NodeCount + Index.Length)
For I = 0 To Index.Length - 1
_NodeCount += 1
If I = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = Index(I)
Up(_NodeCount) = Up(Index(I))
Down(Up(Index(I))) = _NodeCount
Up(Index(I)) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = Index(I)
Next
End Sub
該函式的引數是這一行中值為1的元素的所在列的下標,具體就不再解釋了。和AppendLine函式類似。
在文首的題目中,新增第一行的資料,如下呼叫
AppendLineByIndex(3,5,6)
和AppendLine(0,0,1,0,1,1,0)效果相同。
下面的程式碼是呼叫該類求解文首題目的程式碼
Dim tS As New clsDancingLinks(7)
tS.AppendLineByIndex(3, 5, 6)
tS.AppendLineByIndex(1, 4, 7)
tS.AppendLineByIndex(2, 3, 6)
tS.AppendLineByIndex(1, 4)
tS.AppendLineByIndex(2, 7)
tS.AppendLineByIndex(4, 5, 7)
Dim Ans() As Integer = tS.Dance
Ans()陣列中的值是4,5,1
至此,求解精確覆蓋問題的Dancing Links演算法就介紹完了。利用十字迴圈雙向鏈這個特殊的資料結構,不可思議的完成了快取矩陣和回溯矩陣的過程,十分優雅,十分高效。故Donald E.Knuth把它稱為Dancing Links(舞蹈鏈)。我更喜歡跳躍的舞者這個名字
有很多問題都能轉換為精確覆蓋問題,再利用Dancing Links演算法求解就方便多了。
最後,把該類的完整程式碼貼在下方
Public Class clsDancingLinks
Private Left() As Integer, Right() As Integer, Up() As Integer, Down() As Integer
Private Row() As Integer, Col() As Integer
Private _Head As Integer
Private _Rows As Integer, _Cols As Integer, _NodeCount As Integer
Private Ans() As Integer
Public Sub New(ByVal Cols As Integer)
ReDim Left(Cols), Right(Cols), Up(Cols), Down(Cols), Row(Cols), Col(Cols), Ans(Cols)
Dim I As Integer
Up(0) = 0
Down(0) = 0
Right(0) = 1
Left(0) = Cols
For I = 1 To Cols
Up(I) = I
Down(I) = I
Left(I) = I - 1
Right(I) = I + 1
Col(I) = I
Row(I) = 0
Next
Right(Cols) = 0
_Rows = 0
_Cols = Cols
_NodeCount = Cols
_Head = 0
End Sub
Public Sub AppendLine(ByVal ParamArray Value() As Integer)
_Rows += 1
If Value.Length = 0 Then Exit Sub
Dim I As Integer, K As Integer = 0
For I = 0 To Value.Length - 1
If Value(I) = 1 Then
_NodeCount += 1
ReDim Preserve Left(_NodeCount)
ReDim Preserve Right(_NodeCount)
ReDim Preserve Up(_NodeCount)
ReDim Preserve Down(_NodeCount)
ReDim Preserve Row(_NodeCount)
ReDim Preserve Col(_NodeCount)
ReDim Preserve Ans(_NodeCount)
If K = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
K = 1
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = I + 1
Up(_NodeCount) = Up(I + 1)
Down(Up(I + 1)) = _NodeCount
Up(I + 1) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = I + 1
End If
Next
End Sub
Public Sub AppendLineByIndex(ByVal ParamArray Index() As Integer)
_Rows += 1
If Index.Length = 0 Then Exit Sub
Dim I As Integer, K As Integer = 0
ReDim Preserve Left(_NodeCount + Index.Length)
ReDim Preserve Right(_NodeCount + Index.Length)
ReDim Preserve Up(_NodeCount + Index.Length)
ReDim Preserve Down(_NodeCount + Index.Length)
ReDim Preserve Row(_NodeCount + Index.Length)
ReDim Preserve Col(_NodeCount + Index.Length)
ReDim Preserve Ans(_NodeCount + Index.Length)
For I = 0 To Index.Length - 1
_NodeCount += 1
If I = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = Index(I)
Up(_NodeCount) = Up(Index(I))
Down(Up(Index(I))) = _NodeCount
Up(Index(I)) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = Index(I)
Next
End Sub
Public Function Dance() As Integer()
Return IIf(Dance(0) = True, Ans, Nothing)
End Function
Private Function Dance(ByVal K As Integer) As Boolean
Dim C1 As Integer = Right(_Head)
If (C1 = _Head) Then
ReDim Preserve Ans(K - 1)
Return True
End If
RemoveCol(C1)
Dim I As Integer, J As Integer
I = Down(C1)
Do While I <> C1
Ans(K) = Row(I)
J = Right(I)
Do While J <> I
RemoveCol(Col(J))
J = Right(J)
Loop
If Dance(K + 1) Then Return True
J = Left(I)
Do While J <> I
ResumeCol(Col(J))
J = Left(J)
Loop
I = Down(I)
Loop
ResumeCol(C1)
Return False
End Function
Public Sub RemoveCol(ByVal Col As Integer)
Left(Right(Col)) = Left(Col)
Right(Left(Col)) = Right(Col)
Dim I As Integer, J As Integer
I = Down(Col)
Do While I <> Col
J = Right(I)
Do While J <> I
Up(Down(J)) = Up(J)
Down(Up(J)) = Down(J)
J = Right(J)
Loop
I = Down(I)
Loop
End Sub
Public Sub ResumeCol(ByVal Col As Integer)
Left(Right(Col)) = Col
Right(Left(Col)) = Col
Dim I As Integer, J As Integer
I = Up(Col)
Do While (I <> Col)
J = Right(I)
Do While J <> I
Up(Down(J)) = J
Down(Up(J)) = J
J = Right(J)
Loop
I = Up(I)
Loop
End Sub
End Class
相關推薦
跳躍的舞者,舞蹈鏈(Dancing Links)演算法——求解精確覆蓋問題
精確覆蓋問題的定義:給定一個由0-1組成的矩陣,是否能找到一個行的集合,使得集合中每一列都恰好包含一個1 例如:如下的矩陣 就包含了這樣一個集合(第1、4、5行) 如何利用給定的矩陣求出相應的行的集合呢?我們採用回溯法 矩陣1: 先假定選擇第1行,如下所示: 如上圖中所示,紅色
演算法實踐——舞蹈鏈(Dancing Links)演算法求解數獨
本文介紹該演算法的實際運用,利用舞蹈鏈(Dancing Links)演算法求解數獨 在前文中可知,舞蹈鏈(Dancing Links)演算法在求解精確覆蓋問題時效率驚人。 那利用舞蹈鏈(Dancing Links)演算法求解數獨問題,實際上就是下面一個流程 1、把數獨問題轉換為精確覆蓋問題 2
【POJ3074】Sudoku DLX(Dancing Links)
puts struct pre i++ 能夠 ring include 為什麽 處理 數獨就要DLX,不然不樂意。 數獨的DLX構造:9*9個點每一個點有9種選擇,這構成了DLX的729行,每行、列、陣有限制,均為9行(/列/陣),然後每行(/列/陣)都有九
【POJ3740】Easy Finding DLX(Dancing Links)精確覆蓋問題
ren .cn string 應該 進行 int 函數 操作 urn 題意:多組數據。每組數據給你幾行數,要求選出當中幾行,使得每一列都有且僅有一個1,詢問是可不可行,或者說能不能找出來。 題解:1、暴搜。2、DLX(Dancing links)。 本文寫的是DLX。算
ZOJ 3209 Treasure Map (Dancing Links)
Treasure MapTime Limit: 2 Seconds Memory Limit: 32768 KB Your boss once had got many copies of a treasure map. Unfortunately, all the copies are now
Dancing Links演算法——求解精確覆蓋問題
轉載自:http://www.cnblogs.com/grenet/p/3145800.html 精確覆蓋問題的定義:給定一個由0-1組成的矩陣,是否能找到一個行的集合,使得集合中每一列都恰好包含一個1 例如:如下的矩陣 就包含了這樣一個集合(第1、4、5行) &n
Exact cover (Dancing Links 模板題)
1017 - Exact cover 時間限制:15秒 記憶體限制:128兆 自定評測 5584 次提交 2975 次通過 題目描述There is an
Dubbo 結合 Spring Boot 的探索(註冊發現,管理監控,全鏈路日誌跟蹤)
dubboot-example 探索dubbo 和 spring boot 的結合, 採用https://github.com/dubbo/dubbo-spring-boot-project 來實現dubbo和spring boot的結合。(新的Spring
APP,Web Application(Web APP)等概念講解
webapp app 博文說明【前言】: 本文將通過個人口吻介紹APP,Web Application相關知識,在目前時間點【2017年5月14號】下,所掌握的技術水平有限,可能會存在不少知識理解不夠深入或全面,望大家指出問題共同交流,在後續工作及學習中如發現本文內容與實際情況有所偏差,將會完善
[luoguP1972] [SDOI2009]HH的項鏈(莫隊)
include -m span 適合 data style 我們 pre 總結 傳送門 莫隊基礎題,適合我這種初學者。 莫隊是離線算法,通常不帶修改,時間復雜度為 O(n√n) 我們要先保證通過 [ l , r ] 求得 [ l , r + 1 ]
Java棧,PC寄存器,本地方法棧,堆,方法區(靜態區)和運行常量池
局部變量 fan log 變量 實例 分析 創建 china java棧 https://my.oschina.net/wangsifangyuan/blog/711329 前言:當要判斷一個變量存在什麽空間上時,先分析它是哪一種(是實例變量還是局部變量),實例變量存在於所
thinkPHP使用中踩的坑,記錄一下(不停更)
切換 合法性 問題 table 字符串 mode true use data 版本3.2.3 1、數據庫操作中的連貫操作table(),在查詢的時候可以切換表,但是在插入,更新的時候請不要使用。例如 D(‘user‘)->table(‘auth‘)->add(
求橋,割點(HihoCoder - 1183 )
tar mem name using ems n) mes hihocoder ins #include<cstdio>#include<cstring>#include<algorithm>using namespace std;str
正向代理,反向代理(圖片解析)
vpd pro sha ado oss 分享 ffffff 技術 ges 正向代理,反向代理(圖片解析)
【BZOJ】1878: [SDOI2009]HH的項鏈 (主席樹)
莫隊 color amp span void == 常數 不同 d+ 題目 傳送門:QWQ 分析 莫隊也能做,但我想練練主席樹。 求k-th一樣維護第i個時候的線段樹,線段樹來維護區間不同數。 然後查詢時可以通過上下界小優化一波。 但是我的代碼醜陋
python---django中orm的使用(4)字段,參數(on_delete重點)補充
protect 設置 lean 速度 str through 存在 也會 ren 1.索引: 普通索引:加快查找速度 唯一索引:加快查找速度,唯一約束 主鍵索引:加快查找速度,唯一索引,不為空 class UserInfo(models.Model): user
DataFrame基本操作 <三> 計算名次,移除重復數據,數據替換,劃分區間,分組統計(變成類)
pla cti 特定 但是 afr bin 條件 IV 用法 生成一個實例 df5 = DataFrame({‘b‘: [4.3, 7, -3, 2], ‘a‘: [0, 1, 0, 1], ‘c‘: [
小白學習之路,基礎三(函數)
但是 iter 使用 問題 個數 函數作為參數 無限 中間 ble 一,函數的基本介紹 首先談到函數,相信大家都不陌生,不管是其他語言都會用到,可能就是叫法不一樣。就我知道的跟python中函數類似的,在C中只有function,在Java裏面叫做method,在js中也是
服務器Centos7.4 下jdk1.8環境配置、mysql環境搭建,mysql找回(重置)密碼看這篇就夠了
版本 jdk下載 改密 我們 完成 eight ati html wid 最近一直幫我的同學搭建自己的服務器,其中涉及到了以下知識點,經過查詢博客資料等方式,再加上多重實踐,我成功總結出了完整的配置一個簡單服務器環境的步驟: (來自 ZYXS 的CSDN 博客 ,全文地址請
HDU 2191 - 悼念512汶川大地震遇難同胞——珍惜現在,感恩生活 (多重揹包)
題目 急!災區的食物依然短缺! 為了挽救災區同胞的生命,心繫災區同胞的CK準備自己採購一些糧食支援災區,現在假設CK一共有資金n元,而市場有m種大米,每種大米都是袋裝產品,其價格不等,並且只能整袋購買。 請問:CK能用有限的資金最多能採購多少公斤糧食呢? Input 輸入資料首先

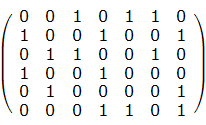
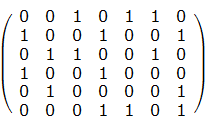
![clip_image002[4] clip_image002[4]](https://images0.cnblogs.com/blog/93227/201306/20141206-3b4bd7db79394066a3b1fb416caab2f5.png)
![clip_image002[6] clip_image002[6]](https://images0.cnblogs.com/blog/93227/201306/20141210-51c3f91ceebe404d89c8b70adf1b9909.png)
![clip_image002[8] clip_image002[8]](https://images0.cnblogs.com/blog/93227/201306/20144122-518a2ef670d0491794eebaa7da2f2f98.png)
![clip_image002[10] clip_image002[10]](https://images0.cnblogs.com/blog/93227/201306/20144122-a9c55df3ed704ed78f1f471a3d82de05.png)