[LeetCode] Domino and Tromino Tiling 多米諾和三格骨牌
We have two types of tiles: a 2x1 domino shape, and an "L" tromino shape. These shapes may be rotated.
XX <- domino XX <- "L" tromino X
Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.
(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)
Example: Input: 3 Output: 5 Explanation: The five different ways are listed below, different letters indicates different tiles: XYZ XXZ XYY XXY XYY XYZ YYZ XZZ XYY XXY
Note:
- N will be in range
[1, 1000].
這道題是關於多米諾骨牌和三格骨牌的,其中由兩個方形格子組成的是多米諾骨牌(音譯,即為雙格骨牌),而由三個方形格子組成的‘L’型的是三格骨牌,但其實本質還是個拼格子的問題,並沒有利用到骨牌酷炫的連倒技能,倒反而更像是俄羅斯方塊中的形狀。說是有一個2xN大小的棋盤,我們需要用這些多米諾和三格骨牌來將棋盤填滿,問有多少種不同的填充方法,結果需要對一個超大數取餘。那麼根據博主多年的經驗,對於這種求極值,並且超大的情況下,只能使用動態規劃Dynamic Programming來做,什麼暴力遞迴神馬的,等著爆棧吧。
既然決定了要用DP來做,那麼首先就來設計dp陣列吧,這裡我們就用一個一維的dp陣列就行了,其中dp[i]表示填滿前i列的不同填法總數對超大數10e^9+7取餘後的結果。那麼DP解法的難點就是求狀態轉移方程了,沒什麼太好的思路的時候,就從最簡單的情況開始羅列吧。題目中給了N的範圍是[1, 1000],那麼我們來看:
當N=1時,那麼就是一個2x1大小的棋盤,只能放一個多米諾骨牌,只有一種情況。
當N=2時,那麼就是一個2x2大小的棋盤,如下圖所示,我們有兩種放置方法,可以將兩個多米諾骨牌豎著並排放,或者是將其橫著並排放。
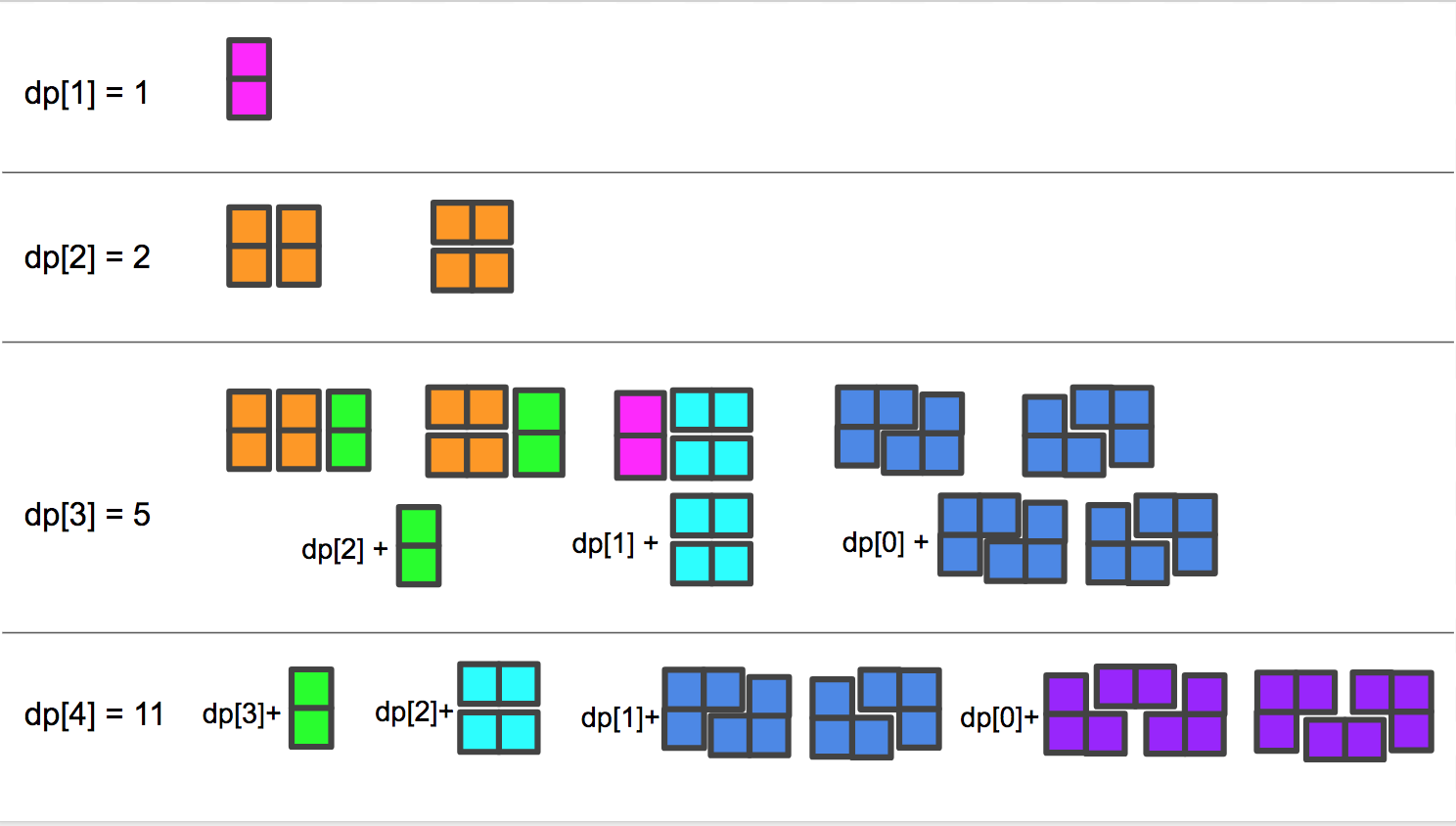
當N=3時,那麼就是一個3x2大小的棋盤,我們共用五種放置方法,如下圖所示。仔細觀察這五種情況,我們發現其時時跟上面的情況有聯絡的。前兩種情況其實是N=2的兩種情況後面加上了一個豎著的多米諾骨牌,第三種情況其實是N=1的那種情況後面加上了兩個平行的橫向的多米諾骨牌,後兩種情況是N=0(空集)再加上兩種三格骨牌對角擺開的情況。
當N=4時,那麼就是一個4x2大小的棋盤,我們共用十一種放置方法,太多了就不一一畫出來了,但是其也是由之前的情況組合而成的。首先是N=3的所有情況後面加上一個豎著多米諾骨牌,然後是N=2的所有情況加上兩個平行的橫向的多米諾骨牌,然後N=1再加上兩種三格骨牌對角擺開的情況,然後N=0(空集)再加上兩種三格骨牌和一個橫向多米諾骨牌組成的情況。
N=5的情況博主沒有再畫了,可以參見ZhengKaiWei大神的帖子中的手稿圖,很萌~
根據目前的狀況,我們可以總結一個很重要的規律,就是dp[n]是由之前的dp值組成的,其中 dp[n-1] 和 dp[n-2] 各自能貢獻一種組成方式,而dp[n-3],一直到dp[0],都能各自貢獻兩種組成方式,所以狀態轉移方程呼之欲出:
dp[n] = dp[n-1] + dp[n-2] + 2 * (dp[n-3] + ... + dp[0])
= dp[n-1] + dp[n-3] + dp[n-2] + dp[n-3] + 2 * (dp[n-4] + ... dp[0])
= dp[n-1] + dp[n-3] + dp[n-1]
= 2 * dp[n-1] + dp[n-3]
最後化簡後的形式就是最終的狀態轉移方程了,是不是叼的飛起~
class Solution { public: int numTilings(int N) { int M = 1e9 + 7; vector<long> dp(N + 1); dp[0] = 1; dp[1] = 1; dp[2] = 2; for (int i = 3; i <= N; ++i) { dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % M; } return dp[N]; } };
參考資料:
