$多米諾骨牌$

Description

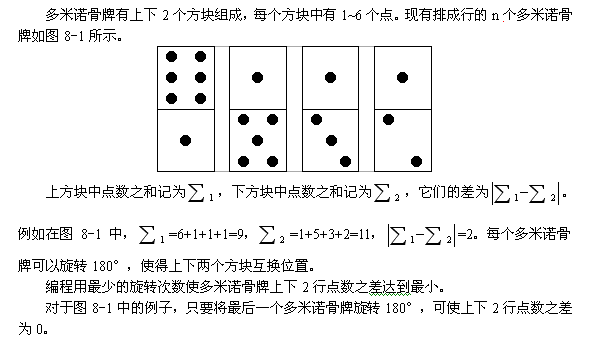
Input

輸入檔案的第一行是一個正整數n(1≤n≤1000)，表示多米諾骨牌數。接下來的n行表示n個多米諾骨牌的點數。每行有兩個用空格隔開的正整數，表示多米諾骨牌上下方塊中的點數a和b，且1≤a，b≤6。

Output

輸出檔案僅一行，包含一個整數。表示求得的最小旋轉次數。

Sample Input

4

6 1

1 5

1 3

1 2

Sample Output

１

題目大意：

有n個骨牌，每個骨牌上面和下面都有一個1~6的數，每個骨牌可以上下翻轉，使上下數字反轉，最少翻幾次可以使上面數的總和與下面數的總和的差最少

解題思路：

用一個二維陣列f[i][j]來表示前i個骨牌上數減下數（上數：上面的數加在一起，下數：下面的數加在一起）為j時翻轉的最少次數，每一個骨牌不翻時為-上面的數+下面的數(因為遞推要倒著推)，翻時為+上面的數-下面的數，然後遞推出結果

動態轉移方程：

$f\left[i\right]\left[j\right]=m$

i n { f [ i − 1 ] [ j − a [ i ] + b [ i ] ] f [ i − 1 ] [ j + a [ i ] − b [ i ] ] + 1 f[i][j]=min\left\{\begin{matrix}f[i-1][j-a[i]+b[i]]\\ f[i-1][j+a[i]-b[i]]+1\end{matrix}\right.

第一次AC的程式碼：

#include<cstdio>
#include<iostream>
#include<cstring>
#define M 6000//設定上限
using namespace std;
int n,k,a[1002],b[1001],f[1001][12010];
int main()
{
	memset(f,127/3,sizeof(f));//用min時要先賦一個較大的值
	scanf("%d",&n);
	f[0][M]=0;//初值，從0開始，因為有負數，所以從M開始，上限是12000（6000），下限是0（-6000）
	for (int i=1;i<=n;i++)
	  scanf("%d%d",&a[i],&b[i]);
	for (int i=1;i<=n;i++)
	  for (int j=1;j<=M*2;j++)//正負數都要
	    f[i][j]=min(f[i-1][j-a[i]+b[i]],f[i-1][j+a[i]-b[i]]+1);//前面的是不翻，後面的是翻
	k=M;//從0開始
	while (f[n][k]==f[0][1]) k++;//f[0][1]為一開始的值，有變化時說明可以翻成差值為k
	printf("%d",f[n][k]);//輸出
}

優化後的程式碼：

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int n,M,k,a[1002],b[1001],f[1001][12005];
int main()
{
	memset(f,127/3,sizeof(f));
	scanf("%d",&n);
	M=n*6;//變化主要有M，因為大於n*6的都沒有用，所以這樣可以省時間
	f[0][M]=0;
	for (int i=1;i<=n;i++)
	  {
	  	scanf("%d%d",&a[i],&b[i]);//塞在一起
		for (int j=M-i*6;j<=M+i*6;j++)//第一次的範圍是-6~6，第二次是-12~12，從M開始，當i加一時，上下的限制各加一，可以省很多時間
	      f[i][j]=min(f[i-1][j-a[i]+b[i]],f[i-1][j+a[i]-b[i]]+1);//動態轉移方程
	  }
	k=M;
	while (f[n][k]==f[0][1]) k++;
	printf("%d",f[n][k]);
}