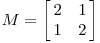SVD實際上是數學專業內容，但它現在已經滲入到不同的領域中。SVD的過程不是很好理解，因為它不夠直觀，但它對矩陣分解的效果卻非常好。比如，Netflix（一個提供線上電影租賃的公司）曾經就懸賞100萬美金，如果誰能提高它的電影推薦系統評分預測準確率提高10%的話。令人驚訝的是，這個目標充滿了挑戰，來自世界各地的團隊運用了各種不同的技術。最終的獲勝隊伍"BellKor's Pragmatic Chaos"採用的核心演算法就是基於SVD。

SVD提供了一種非常便捷的矩陣分解方式，能夠發現數據中十分有意思的潛在模式。在這篇文章中，我們將會提供對SVD幾何上的理解和一些簡單的應用例項。

線性變換的幾何意義(The geometry of linear transformations)

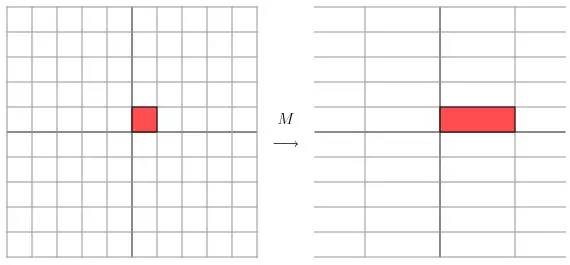
讓我們來看一些簡單的線性變換例子，以 2 X 2 的線性變換矩陣為例，首先來看一個較為特殊的，對角矩陣：

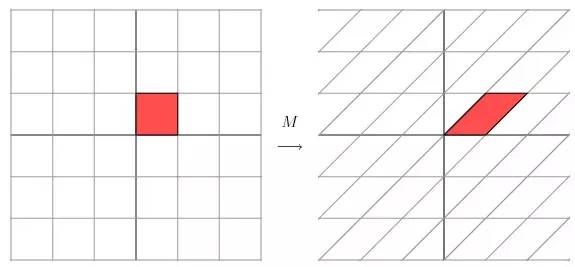
從幾何上講，M 是將二維平面上的點(x,y)經過線性變換到另外一個點的變換矩陣，如下圖所示

變換的效果如下圖所示，變換後的平面僅僅是沿 X 水平方面進行了拉伸3倍，垂直方向是並沒有發生變化。

現在看下矩陣

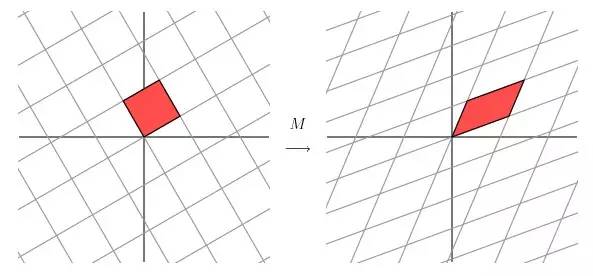
這個矩陣產生的變換效果如下圖所示

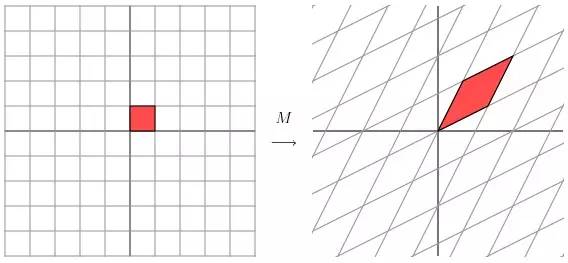
這種變換效果看起來非常的奇怪，在實際環境下很難描述出來變換的規律 ( 這裡應該是指無法清晰辨識出旋轉的角度，拉伸的倍數之類的資訊)。還是基於上面的對稱矩陣，假設我們把左邊的平面旋轉45度角，然後再進行矩陣 M 的線性變換，效果如下圖所示：

看起來是不是有點熟悉？ 對的，經過 M 線性變換後，跟前面的對角矩陣的功能是相同的，都是將網格沿著一個方向拉伸了3倍。

這裡的 M 是一個特例，因為它是對稱的。非特殊的就是我們在實際應用中經常遇見一些 非對稱的，非方陣的矩陣。如上圖所示，如果我們有一個 2 X 2 的對稱矩陣 M 的話，我們先將網格平面旋轉一定的角度，M 的變換效果就是在兩個維度上進行拉伸變換了。

用更加數學的方式進行表示的話，給定一個對稱矩陣 M ，我們可以找到一些相互正交 Vi ，滿足 MVi 就是沿著 Vi 方向的拉伸變換，公式如下：

Mvi = λivi

這裡的 λi 是拉伸尺度(scalar)。從幾何上看，M 對向量 Vi 進行了拉伸，對映變換。Vi 稱作矩陣 M 的特徵向量(eigenvector)， λi 稱作為矩陣 M 特徵值(eigenvalue)。這裡有一個非常重要的定理，對稱矩陣 M 的特徵向量是相互正交的。

如果我們用這些特徵向量對網格平面進行線性變換的話，再通過 M 矩陣對網格平面進行線性換的效果跟對 M 矩陣的特徵向量進行線性變換的效果是一樣的。

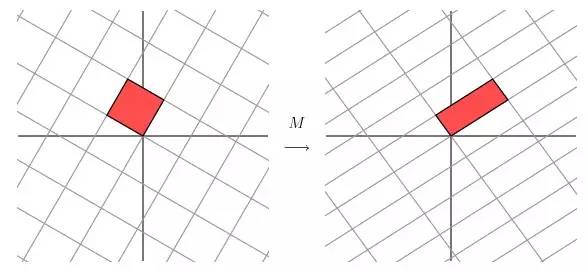
對於更為普通的矩陣而言，我們該怎麼做才能讓一個原來就是相互垂直的網格平面(orthogonal grid), 線性變換成另外一個網格平面同樣垂直呢？PS：這裡的垂直如圖所示，就是兩根交錯的線條是垂直的。

經過上述矩陣變換以後的效果如圖

從圖中可以看出，並沒有達到我們想要的效果。我們把網格平面旋轉 30 度角的話，然後再進行同樣的線性變換以後的效果，如下圖所示

讓我們來看下網格平面旋轉60度角的時候的效果。

嗯嗯，這個看起來挺不錯的樣子。如果在精確一點的話，應該把網格平面旋轉 58.28 度才能達到理想的效果。