奇異值分解( The singular value decomposition )

  該部分是從幾何層面上去理解二維的SVD：對於任意的 2 x 2 矩陣，通過SVD可以將一個相互垂直的網格(orthogonal grid)變換到另外一個相互垂直的網格。

  我們可以通過向量的方式來描述這個事實: 首先，選擇兩個相互正交的單位向量v₁ 和v₂,向量Mv₁和Mv₂正交。

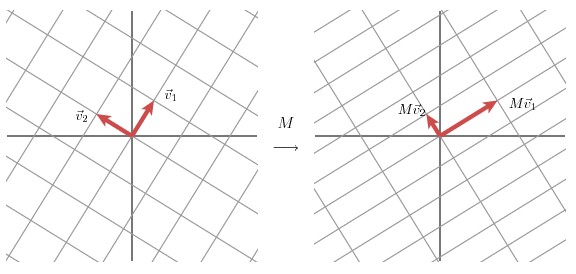
     u₁和u₂分別表示Mv₁和Mv₂的單位向量，σ₁*u₁=Mv₁和σ₂*u₂=Mv_2 。σ₁和σ₂分別表示這不同方向向量上的模，也稱作為矩陣M的奇異值。

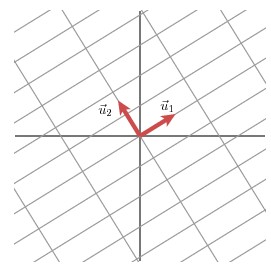
  這樣我們就有了如下關係式

Mv₁ = σ

  我們現在可以簡單描述下經過M線性變換後的向量x的表達形式。由於向量v₁和v₂是正交的單位向量，我們可以得到如下式子：

x = (v₁x) v₁ + (v₂x) v₂

  這就意味著：

Mx = (v₁x) Mv₁ + (v₂x) Mv₂
Mx = (v₁x) σ₁u₁ + (v₂x) σ₂u₂

  向量內積可以用向量的轉置來表示，如下所示

vx = v^Tx

  最終的式子為

Mx = u₁σ₁v₁^Tx + u₂σ₂v₂^Tx
M = u₁σ₁v₁^T + u₂σ₂v₂^T

  上述的式子經常表示成

M = UΣV^T

    u 矩陣的列向量分別是u₁

  這就表明任意的矩陣 M 是可以分解成三個矩陣。V 表示了原始域的標準正交基，u 表示經過M 變換後的co-domain的標準正交基，Σ 表示了V 中的向量與u 中 相對應向量之間的關係。(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.)

如何獲得奇異值分解？( How do we find the singular decomposition? )

  事實上我們可以找到任何矩陣的奇異值分解，那麼我們是如何做到的呢？假設在原始域中有一個單位圓，如下圖所示。經過M 矩陣變換以後在co-domain中單位圓會變成一個橢圓，它的長軸(Mv₁)和短軸(Mv₂)分別對應轉換後的兩個標準正交向量，也是在橢圓範圍內最長和最短的兩個向量。

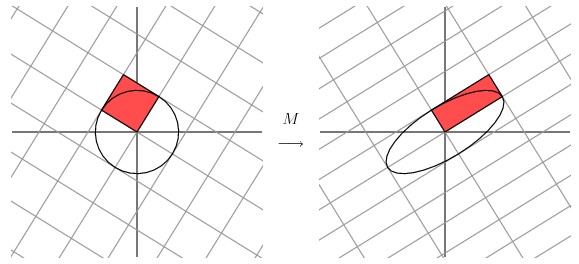
  換句話說，定義在單位圓上的函式|Mx|分別在v₁和v₂方向上取得最大和最小值。這樣我們就把尋找矩陣的奇異值分解過程縮小到了優化函式|Mx|上了。結果發現（具體的推到過程這裡就不詳細介紹了）這個函式取得最優值的向量分別是矩陣 MT M 的特徵向量。由於MTM是對稱矩陣，因此不同特徵值對應的特徵向量都是互相正交的，我們用vi 表示MTM的所有特徵向量。奇異值σ_i = |Mv_i|，向量u_i為Mv_i方向上的單位向量。但為什麼u_i也是正交的呢？

推導如下：

    σ_i和σ_j分別是不同兩個奇異值

Mv_i = σ_iu_i
Mv_j = σ_ju_j.

  我們先看下Mv_iMv_j，並假設它們分別對應的奇異值都不為零。一方面這個表達的值為0，推導如下

Mv_iMv_j = v_i^TM^TMv_j = v_iM^TMv_j = λ_jv_iv_j = 0

  另一方面，我們有

Mv_iMv_j = σ_iσ_ju_iu_j = 0

  因此，u_i和u_j是正交的。但實際上，這並非是求解奇異值的方法，效率會非常低。這裡也主要不是討論如何求解奇異值，為了演示方便，採用的都是二階矩陣。

應用例項(Another example)

  現在我們來看幾個例項。

例項一

  經過這個矩陣變換後的效果如下圖所示

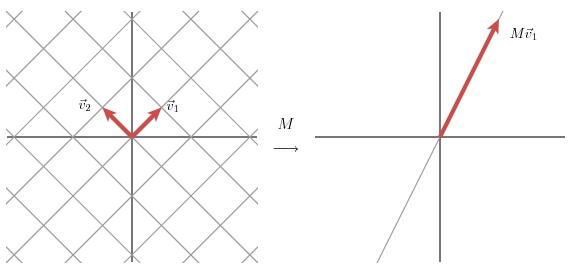
  在這個例子中，第二個奇異值為 0，因此經過變換後只有一個方向上有表達。

M = u₁σ₁v₁^T.

  換句話說，如果某些奇異值非常小的話，其相對應的幾項就可以不同出現在矩陣 M 的分解式中。因此，我們可以看到矩陣 M 的秩的大小等於非零奇異值的個數。

例項二

  我們來看一個奇異值分解在資料表達上的應用。假設我們有如下的一張 15 x 25 的影象資料。

  如圖所示，該影象主要由下面三部分構成。

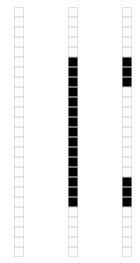
  我們將影象表示成 15 x 25 的矩陣，矩陣的元素對應著影象的不同畫素，如果畫素是白色的話，就取 1，黑色的就取 0. 我們得到了一個具有375個元素的矩陣，如下圖所示

  如果我們對矩陣M進行奇異值分解以後，得到奇異值分別是

σ₁ = 14.72 
σ₂ = 5.22 
σ₃ = 3.31

  矩陣M就可以表示成

M=u₁σ₁v₁^T + u₂σ₂v₂^T + u₃σ₃v₃^T

   v_i具有15個元素，u_i具有25個元素，σ_i對應不同的奇異值。如上圖所示，我們就可以用123個元素來表示具有375個元素的影象資料了。

例項三 減噪(noise reduction)

  前面的例子的奇異值都不為零，或者都還算比較大，下面我們來探索一下擁有零或者非常小的奇異值的情況。通常來講，大的奇異值對應的部分會包含更多的資訊。比如，我們有一張掃描的，帶有噪聲的影象，如下圖所示

  我們採用跟例項二相同的處理方式處理該掃描影象。得到影象矩陣的奇異值：

σ₁ = 14.15 
σ₂ = 4.67 
σ₃ = 3.00 
σ₄ = 0.21 
σ₅ = 0.19 
... 
σ₁₅ = 0.05

  很明顯，前面三個奇異值遠遠比後面的奇異值要大，這樣矩陣M的分解方式就可以如下：

M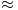u₁σ₁v₁^T + u₂σ₂v₂^T + u₃σ₃v₃^T

  經過奇異值分解後，我們得到了一張降噪後的影象。

例項四 資料分析(data analysis)

  我們蒐集的資料中總是存在噪聲：無論採用的裝置多精密，方法有多好，總是會存在一些誤差的。如果你們還記得上文提到的，大的奇異值對應了矩陣中的主要資訊的話，運用SVD進行資料分析，提取其中的主要部分的話，還是相當合理的。

  作為例子，假如我們蒐集的資料如下所示：

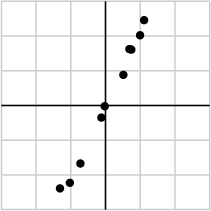
  我們將資料用矩陣的形式表示：

  經過奇異值分解後，得到

σ₁ = 6.04 
σ₂ = 0.22

  由於第一個奇異值遠比第二個要大，資料中有包含一些噪聲，第二個奇異值在原始矩陣分解相對應的部分可以忽略。經過SVD分解後，保留了主要樣本點如圖所示

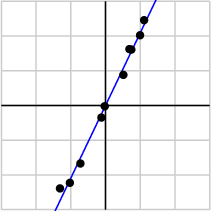
  就保留主要樣本資料來看，該過程跟PCA( principal component analysis)技術有一些聯絡，PCA也使用了SVD去檢測資料間依賴和冗餘資訊.

總結(Summary)

  這篇文章非常的清晰的講解了SVD的幾何意義，不僅從數學的角度，還聯絡了幾個應用例項形象的論述了SVD是如何發現數據中主要資訊的。在 netflix prize中許多團隊都運用了矩陣分解的技術，該技術就來源於SVD的分解思想，矩陣分解算是SVD的變形，但思想還是一致的。之前算是能夠運用矩陣分解 技術於個性化推薦系統中，但理解起來不夠直觀，閱讀原文後醍醐灌頂，我想就從SVD能夠發現數據中的主要資訊的思路，就幾個方面去思考下如何利用資料中所 蘊含的潛在關係去探索個性化推薦系統。也希望路過的各位大俠不吝分享呀。

References:

Gilbert Strang, Linear Algebra and Its Applications. Brooks Cole

William H. Press et al, Numercial Recipes in C: The Art of Scientific Computing. Cambridge University Press.