凱利公式：

f* = (bp - q) / b

其中，f* = 投注金額佔總資金的比例

p = 獲勝的概率

q = 失敗的概率，q = 1-p

b = 賠率

假設：你輸和贏的概率均為是50%，例如拋硬幣。贏的時候淨收益率為1，即rw=1，輸的時候淨損失率為0.5，即rl=0.5。也就是說當你每投入1元錢，贏的時候你能贏1元，輸的時候你需要付出去5毛。

容易看出該假設下的期望收益是0.25。

根據凱利公式，我們可以得到每局最佳的下注比例為：

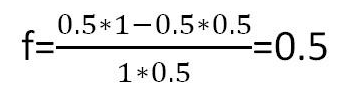
也就是說每次把一半的錢拿去下注，長期來看可以得到最大的收益。

結論一：在經過相同次的局數之後，最後的結果只與在這些局數中贏的局數的數量和輸的局數的數量有關，而與在這些局數中贏的局和輸的局的順序無關。

凱利公式指明瞭風險控制的至關重要性：即便是正期望值的遊戲也不能押太大的賭注。

從數學上講，押注資金比例超過了凱利值，長期的贏錢速度反而下降，還會大大增加出現災難性損失的可能性。 舉個極端的例子，如果你每手都押上全部資金，那麼不管你贏過多少錢，只要輸一次就立刻破產。辛辛苦苦幾十年，一夜回到解放前。

-------------------------

在《低風險投資之路》書中有凱利公式：
F=（Pw*R-Pl)/Rw R是賠率，Pw是勝率,Pl是敗率，F是現有資金下次下注的比例，可以理解為股票的倉位
但是這個版本是簡化的公式，主要用於賭博。

完整的公式：
F=(Pw*Rw-Pl*Rl)/(Rw*Rl)
=預期收益率/(Rw*Rl)
=Pw/Rl-Pl/Rw

DAVID：對於低風險投資者來講，並不該拒絕有風險的品種，甚至不必拒絕高風險品種，只要控制好倉位，都可以將其變成低風險投資組合

--------------------------

假設賭局1：你贏的概率是60%，輸的概率是40%。贏時的淨收益率是100%，輸時的虧損率也是100%。也即：如果贏，那麼你每賭1元可以贏得1元；如果輸，則每賭1元將會輸掉1元。賭局可以進行無限次，每次下的賭注由你自己任意定。問題：假設你的初始資金是100元，那麼怎麼樣下注？即：每次下注金額佔本金的百分之多少，才能使得長期收益最大？
     對於這個賭局，每次下注的期望收益是下注金額的60%*1-40%*1=20%，期望收益為正。也就是說這是一個對賭客佔優的賭局，而且佔的優勢非常大。

其中f為最優的下注比例，p為贏的概率，rw是贏時的淨收益率，例如在賭局1中rw=1。rl是輸時的淨損失率，例如在賭局1中rl=1。(注意此處rl>0。)
根據凱利公式，可以計算出在賭局1中的最有下注比例是20%。

那麼我們應該怎麼樣下注呢？

如果不進行嚴密的思考，粗略的想象一下，我們會覺得既然我每次賭的期望收益是20%，那麼為了實現長期的最大收益，我應該在每次賭博中儘量放入更多比例的本金。這個比例的最大值是100%。

但是顯然每一局賭博都放入100%的本金是不合理的，因為一旦哪一次賭博賭輸了，那麼所有的本金就會全部輸光，再也不能參加下一局，只能黯然離場。而從長期來看，賭輸一次這個事件必然發生，所以說長期來看必定破產。

所以這裡就得出了一個結論：只要一個賭局存在一下子把本金全部輸光的可能，哪怕這個可能非常的小，那麼就永遠不能滿倉。因為長期來看，小概率事件必然發生，而且在現實生活中，小概率事件發生的實際概率要遠遠的大於它的理論概率。這就是金融學中的肥尾效應。