softmax函式詳解
答案來自專欄：機器學習演算法與自然語言處理
這幾天學習了一下softmax啟用函式，以及它的梯度求導過程，整理一下便於分享和交流。
softmax函式
softmax用於多分類過程中，它將多個神經元的輸出，對映到（0,1）區間內，可以看成概率來理解，從而來進行多分類！
假設我們有一個數組，V，Vi表示V中的第i個元素，那麼這個元素的softmax值就是
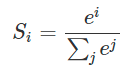
更形象的如下圖表示：
softmax直白來說就是將原來輸出是3,1,-3通過softmax函式一作用，就對映成為(0,1)的值，而這些值的累和為1（滿足概率的性質），那麼我們就可以將它理解成概率，在最後選取輸出結點的時候，我們就可以選取概率最大（也就是值對應最大的）結點，作為我們的預測目標！
舉一個我最近碰到利用softmax的例子：我現在要實現基於神經網路的句法分析器。用到是基於轉移系統來做，那麼神經網路的用途就是幫我預測我這一個狀態將要進行的動作是什麼？比如有10個輸出神經元，那麼就有10個動作，1動作，2動作，3動作...一直到10動作。（這裡涉及到nlp的知識，大家不用管，只要知道我現在根據每個狀態（輸入），來預測動作（得到概率最大的輸出），最終得到的一系列動作序列就可以完成我的任務即可）
原理圖如下圖所示：
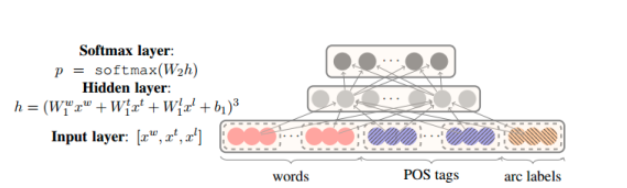
那麼比如在一次的輸出過程中輸出結點的值是如下：
[0.2,0.1,0.05,0.1,0.2,0.02,0.08,0.01,0.01,0.23]
那麼我們就知道這次我選取的動作是動作10，因為0.23是這次概率最大的，那麼怎麼理解多分類呢？很容易，如果你想選取倆個動作，那麼就找概率最大的倆個值即可~（這裡只是簡單的告訴大家softmax在實際問題中一般怎麼應用）
softmax相關求導
當我們對分類的Loss進行改進的時候，我們要通過梯度下降，每次優化一個step大小的梯度，這個時候我們就要求Loss對每個權重矩陣的偏導，然後應用鏈式法則。那麼這個過程的第一步，就是對softmax求導傳回去，不用著急，我後面會舉例子非常詳細的說明。在這個過程中，你會發現用了softmax函式之後，梯度求導過程非常非常方便！
下面我們舉出一個簡單例子，原理一樣，目的是為了幫助大家容易理解！
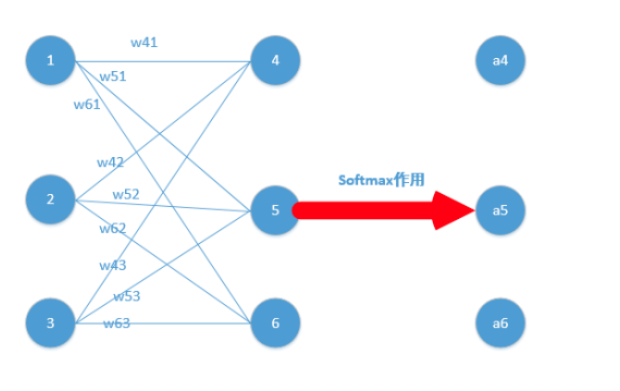
我們能得到下面公式：
z4 = w41*o1+w42*o2+w43*o3
z5 = w51*o1+w52*o2+w53*o3
z6 = w61*o1+w62*o2+w63*o3
z4,z5,z6分別代表結點4,5,6的輸出，01,02,03代表是結點1,2,3往後傳的輸入.
那麼我們可以經過softmax函式得到
好了，我們的重頭戲來了，怎麼根據求梯度，然後利用梯度下降方法更新梯度！
要使用梯度下降，肯定需要一個損失函式，這裡我們使用交叉熵作為我們的損失函式，為什麼使用交叉熵損失函式，不是這篇文章重點，後面有時間會單獨寫一下為什麼要用到交叉熵函式（這裡我們預設選取它作為損失函式）
交叉熵函式形式如下：
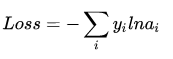
其中y代表我們的真實值，a代表我們softmax求出的值。i代表的是輸出結點的標號！在上面例子，i就可以取值為4,5,6三個結點（當然我這裡只是為了簡單，真實應用中可能有很多結點）
現在看起來是不是感覺複雜了，居然還有累和，然後還要求導，每一個a都是softmax之後的形式！
但是實際上不是這樣的，我們往往在真實中，如果只預測一個結果，那麼在目標中只有一個結點的值為1，比如我認為在該狀態下，我想要輸出的是第四個動作（第四個結點）,那麼訓練資料的輸出就是a4 = 1,a5=0,a6=0，哎呀，這太好了，除了一個為1，其它都是0，那麼所謂的求和符合，就是一個幌子，我可以去掉啦！
為了形式化說明，我這裡認為訓練資料的真實輸出為第j個為1，其它均為0！
那麼Loss就變成了,累和已經去掉了，太好了。現在我們要開始求導數了！
我們在整理一下上面公式，為了更加明白的看出相關變數的關係：
其中,那麼形式變為
那麼形式越來越簡單了，求導分析如下：
引數的形式在該例子中，總共分為w41,w42,w43,w51,w52,w53,w61,w62,w63.這些，那麼比如我要求出w41,w42,w43的偏導，就需要將Loss函式求偏導傳到結點4，然後再利用鏈式法則繼續求導即可，舉個例子此時求w41的偏導為:
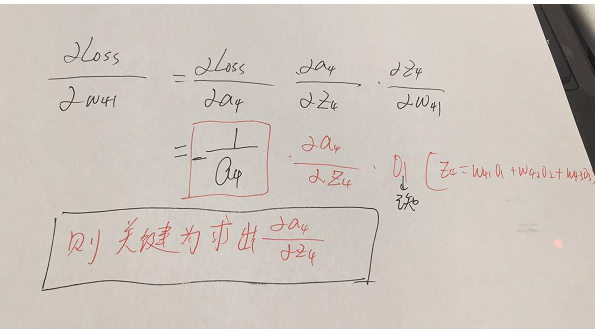
w51.....w63等引數的偏導同理可以求出，那麼我們的關鍵就在於Loss函式對於結點4,5,6的偏導怎麼求，如下：
這裡分為倆種情況：
j=i對應例子裡就是如下圖所示：
比如我選定了j為4，那麼就是說我現在求導傳到4結點這！
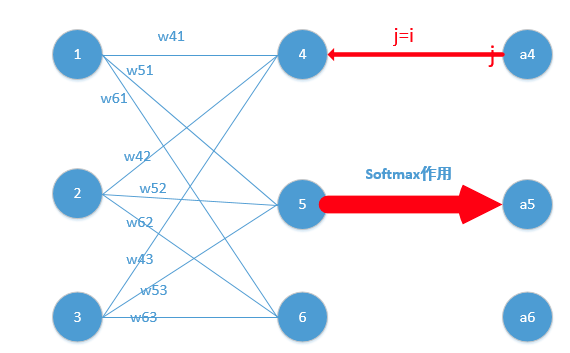
那麼由上面求導結果再乘以交叉熵損失函式求導
，它的導數為
,與上面
相乘為
（形式非常簡單，這說明我只要正向求一次得出結果，然後反向傳梯度的時候，只需要將它結果減1即可，後面還會舉例子！）那麼我們可以得到Loss對於4結點的偏導就求出了了（這裡假定4是我們的預計輸出）
第二種情況為：
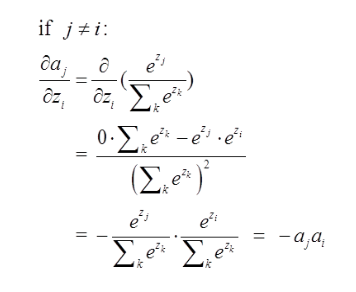
這裡對應我的例子圖如下，我這時對的是j不等於i，往前傳：
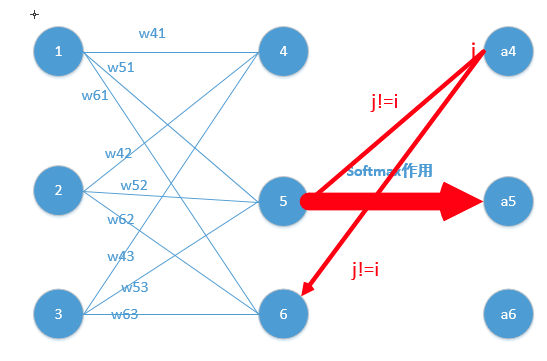
那麼由上面求導結果再乘以交叉熵損失函式求導
，它的導數為
,與上面
相乘為
（形式非常簡單，這說明我只要正向求一次得出結果，然後反向傳梯度的時候，只需要將它結果儲存即可，後續例子會講到）這裡就求出了除4之外的其它所有結點的偏導，然後利用鏈式法則繼續傳遞過去即可！我們的問題也就解決了！
下面我舉個例子來說明為什麼計算會比較方便，給大家一個直觀的理解
舉個例子，通過若干層的計算，最後得到的某個訓練樣本的向量的分數是[ 2, 3, 4 ],
那麼經過softmax函式作用後概率分別就是=[
,
,
] = [0.0903,0.2447,0.665],如果這個樣本正確的分類是第二個的話，那麼計算出來的偏導就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常簡單！！然後再根據這個進行back propagation就可以了
到這裡，這篇文章的內容就講完了，我希望根據自己的理解，通過列出大量例子，直白的給大家講解softmax的相關內容，讓大家少走彎路，真心希望對大家的理解有幫助！歡迎交流指錯！畫圖整理不易，覺得有幫助的給個讚唄，哈哈！
參考：
部分圖片來自於網路！