掌握演算法是作為程式設計師的基本必備素質，而排序也是各種演算法的基礎，雖說java幫我們封裝好了各種資料型別的排序方法，可是我們還是要知道他的原理，下面我就說幾種常用的演算法及原理；

氣泡排序：

原理：相鄰元素兩兩比較，大的往後放，每一次完畢，最大值出現在了最大索引處；
下面我們用圖的方式直觀的給大家展示

從上面的圖來看，每一次比較交換的演算法應該是

/for(int i=0;i<arr.length-1;i++){
 		if(arr[i]>arr[i+1]){
    			//值交換
       			 int t=arr[i];
 				 arr[i]
 
=arr[i+1];
				 arr[i+1]=t;
		  }
}

首次比較五個數我們只需要比較四次；每多一次排序，少比較一次，因此i<arr.length-1；而這個過程我們需要五次的重複，每次我們給迴圈條件 -1;而這也是可以簡化的，所以最後我們優化過後的演算法為：

private static void sort(int[] arr) {
        for(int j=0;j<arr.length;j++){
            for (int i = 0; i <  arr.length - 1 -j ; i++) {
                if
 
 (arr[i] > arr[i + 1]) {
                    //值交換
                    int t = arr[i];
                    arr[i] = arr[i + 1];
                    arr[i + 1] = t;
                }
            }
        }
  }

選擇排序：

原理：每一次那一個元素,和剩餘的元素挨個去比較,經過第一遍比較,那麼最小的元素,或移動到最前面去；

 for (int i = index + 1
 
; i < arr.length; i++) {
                if (arr[index] > arr[i]) {
                	//值交換
                    int t = arr[index];
                    arr[index] = arr[i];
                    arr[i] = t;
                }
            }

選擇排序就是每次選擇一個數和其餘的數一一進行比較，比他大的不動，比他小的兩者交換；第一次我們就是選擇第一個數為基準，它作為index和其餘的比較，而我們第一個比較的數就是第二個數，應為自己和自己比較並沒有意義；然後迴圈比較，每次變數 +1；以上的只是第一次比較，當比較完後，我們換第二個數為基準，即index+1；所以我們將其優化為：

private static void sort2(int[] arr) {
        for (int index = 0; index < arr.length - 1; index++) {
            for (int i = index + 1; i < arr.length; i++) {
                if (arr[index] > arr[i]) {
                    int t = arr[index];
                    arr[index] = arr[i];
                    arr[i] = t;
                }
            }
        }
    }

在外圍再加一層迴圈，它起到的作用就是每次比較過後index自加；

快速排序：

原理：快速排序的原理就是分治法；即先比大小，再分割槽，然後分而治之；
從陣列中取出一個數，作為基準；然後分割槽，選擇出比這個數大的數放到它的右邊，比這個數小的數放到他的左邊；然後分別對左右分割槽進行分割槽，直到每個分割槽只剩一個數；
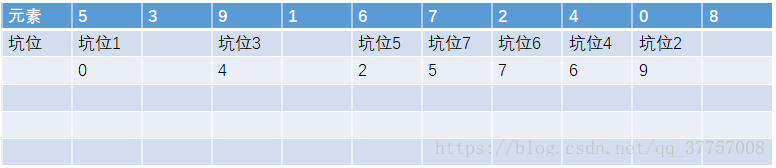
而他的實現思想可以叫做挖坑填數；什麼意思呢？
1.將基準數挖出，形成坑位一；
2.先從後向前找比基準數小的數，找到後挖出它，形成新坑位，將它填到之前的坑位中；
3.然後由前向後找比基準數大的數，找到後挖出它，將他填到之前的坑位中；
4.分號區後，重複之前的2、3步驟；

第一次分析挖坑填數後的結果如下圖：

程式碼實現：
首先我們需要給序列的起始位置和末尾位置，以此確定每次從前向後和從後向前比較的起點；
int i = start;
int j = end;
然後定義基準位置；
int x =arr[i];
最外圍的迴圈條件為i < j,即起點位置小於終點位置，因為我們最後如果起點位置和終點位置一樣時，每個分割槽就只剩一個數了，這樣就完成了排序；同時我們不知道這個過程需要迴圈多少次，於是用while（）迴圈方法；
while（i < j）{}
然後我們就分開從左到右和從右到左的兩部分；
從後往前：
while (i<j&&arr[j]>x){
j–;
}
if(i<j){
arr[i]=arr[j];//挖坑填數
i++; //因為接下來我們要從前往後找了,我們順遍讓i遞增一下
}
從前往後：
while (i < j && arr[i] <= x) {
i++;
}
if (i < j) {
arr[j] = arr[i];//挖坑填數
j–; //因為接下來我們要從後往前找了,我們順遍讓j遞減一下
}
最後我們把基準數填到最後的位置：
arr[i]=x;
同時返回基準數的位置，return i;

我們得到分割槽完後，基準數的左邊的數為左分割槽的end,基準數的右邊的數作為右分割槽的start；

因此最後我們得到的程式碼為：

public class QuickSort {

    public static void sort(int[] arr,int start,int end){
        if(start<end){
            //獲取中間索引
            int index=getIndex(arr,start,end);
            //對左右兩部分進行遞迴呼叫
            sort(arr,start,index-1);//排左半邊
            sort(arr,index+1,end);//排右半邊

        }
    }
    //挖坑填數
    private static int getIndex(int[] arr, int start, int end) {
            int i=start;
            int j=end;
            //定義基準數
            int x=arr[i];
            while (i<j){
                //1.從後往前跟基準數進行比較
                while (i<j&&arr[j] >= x){
                    j--;
                }
                if(i<j){
                    arr[i]=arr[j];//挖坑填數
                    i++;//因為接下來我們要從前往後找了,我們順遍讓i遞增一下
                }
                //2.從前往後找
                while (i < j && arr[i] <= x) {
                    i++;
                }
                if (i < j) {
                    arr[j] = arr[i];//挖坑填數
                    j--;//因為接下來我們要從後往前找了,我們順遍讓j遞減一下
                }

            }
            //把基準數填到最後一個坑位
            arr[i]=x;

        return i;
    }
}

二分法查詢：

注：二分法查詢的前提是元素有序；
原理：每次都查中間的那個元素，比較大或者小就能減少一半的元素；

程式碼實現：
首先我們定義三個位置的變數：
int minIndex=0;
int maxIndex=arr.length-1;
int midIndex=(minIndex+maxIndex)/2;
最外圍迴圈則是最小值小於最大值
minIndex < maxIndex；
如果要查的元素,正好等於中間索引所對應的元素 直接返回這個中間索引；
if (ele == arr[midIndex]) {
return midIndex;
}
如果你要查詢的元素比中間索引所對應的元素大 那麼就動最小索引
if (ele > arr[midIndex]) {
minIndex = midIndex + 1；
}
如果你要查詢的元素比中間索引所對應的元素小,那麼你就動最大索引
if (ele < arr[midIndex]) {
maxIndex = midIndex - 1;
}
最後重新計算中間的索引
midIndex = (minIndex + maxIndex) / 2;

所以最後的程式碼就是：

private static int findIndex2(int[] arr, int ele) {
        int minIndex=0;
        int maxIndex=arr.length-1;
        int midIndex=(minIndex+maxIndex)/2;
        while (minIndex < maxIndex){
            //如果要查的元素,正好等於中間索引所對應的元素 直接返回這個中間索引
            if (ele == arr[midIndex]) {
                return midIndex;
                //如果你要查詢的元素比中間索引所對應的元素大 那麼就動最小索引
            } else if (ele > arr[midIndex]) {

                minIndex = midIndex + 1;
                //如果你要查詢的元素比中間索引所對應的元素小,那麼你就動最大索引
            } else if (ele < arr[midIndex]) {
                maxIndex = midIndex - 1;
            }
            //再重新計算中間索引
            midIndex = (minIndex + maxIndex) / 2;
        }
        return -1;
    }