大家好，我是烤鴨：    

   今天分享一下基礎排序演算法之直接插入排序。

1.     直接插入排序：

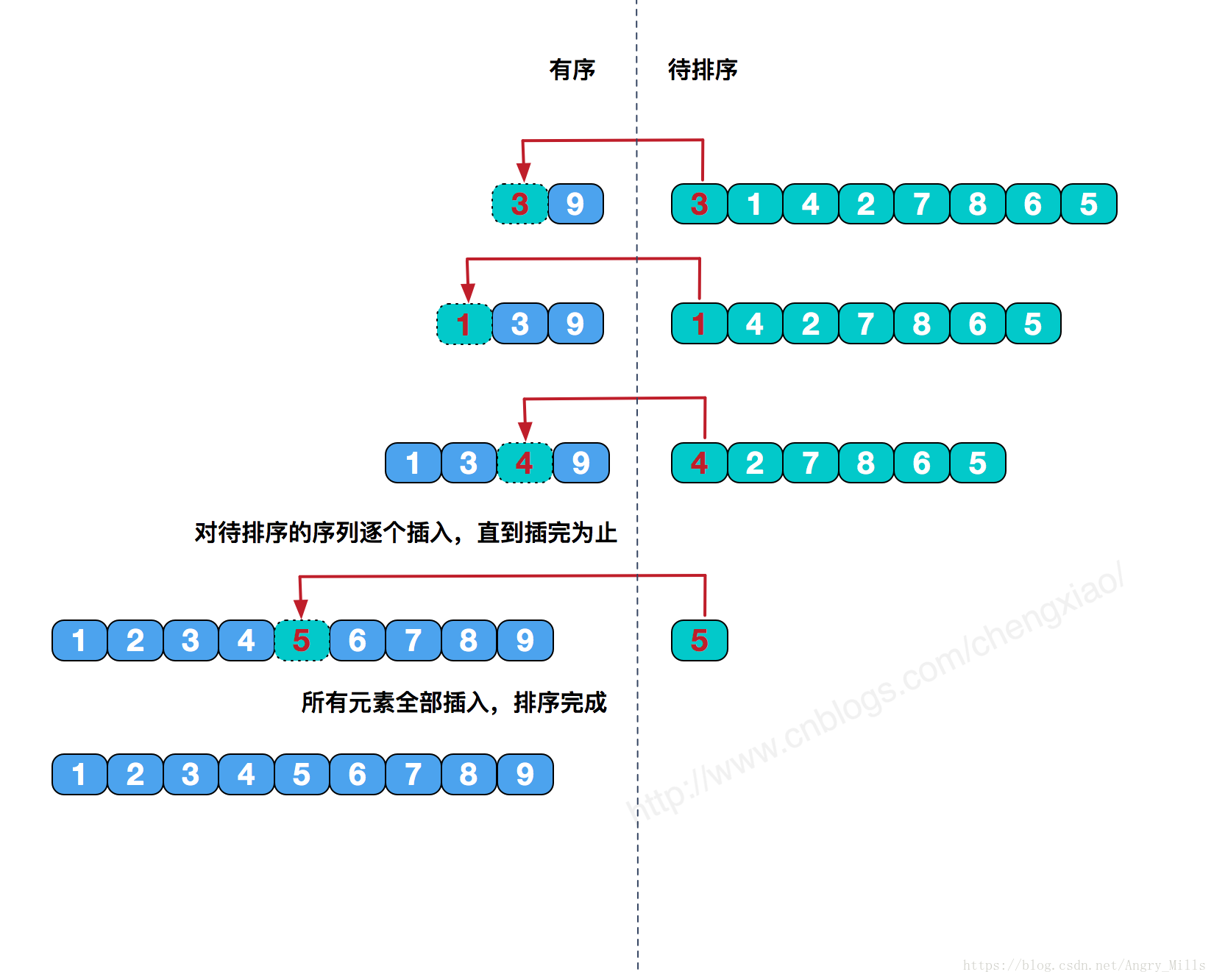
原理：假設前面的數為有序數列，然後有序數列與無序數列的每個數比較，我們可以從右向左比較

思路：從第2個數開始，和1比較。這樣前2個有序。

           第3個和前2個比較，這樣前3個有序。（如果是最小的，則第3個元素處在第1個位置，後面的元素後移1。）

           第4個和前3個比較，同上。

           直到第 n 個元素 和 前 n-1 個比較。

程式碼實現：

    /**
     * 直接插入排序
     * directInsertSort
     *
     * @param array 時間複雜度，O的n^2
     * 直接插入排序就是我們假設前面的數為有序數列，然後有序數列與無序數列的每個數比較，我們可以從右向左比較
     * 當 array[i]<=array[j]=
     */
    public void directInsertSort(int[] array) {
        long nowTime = System.currentTimeMillis();
        int tem = 0;
        for (int i = 1; i < array.length; i++) {
            int j = i - 1;
            tem = array[i];
            for (; j >= 0 && array[j] > tem; j--) {
                array[j + 1] = array[j];//將大於array[i]的數整體後移一單位
            }
            array[j + 1] = tem;
        }
        System.out.println("直接插入排序，花費時間(s):" + ((System.currentTimeMillis() - nowTime) / 1000.0) + "s");
    }
 

2.     折半插入排序（優化）：

思路：

其實和直接插入排序是類似的，只是在遍歷元素的時候採用的是二分法，直插採用的是順序遍歷。

取 temp 作為當前元素，

begin從0開始，end到陣列最後一個元素。

如果temp < 中間值，begin從中間值+1繼續，否則 end 變為 end - 1 繼續，

begin 到 i 整體後移。

如圖：(圖片來源 http://www.cnblogs.com/chengxiao/p/6103002.html)

程式碼實現：

/**
     * 折半插入排序
     * @param source
     * halfInsertSort
     *
     * @param source 時間複雜度，O的n^2
     * 折半插入排序演算法是一種穩定的排序演算法，比直接插入演算法明顯減少了關鍵字之間比較的次數，
     * 因此速度比直接插入排序演算法快，但記錄移動的次數沒有變，所以折半插入排序演算法的時間複雜度仍然為O(n^2)，
     * 與直接插入排序演算法相同
     */
    public static void halfInsertSort(int[] source) {
        long nowTime = System.currentTimeMillis();
        int size = source.length;
        for (int i = 1; i < size; i++) {
            // 拿出來
            int temp = source[i];
            int begin = 0; // 標記排好序的陣列的頭部
            int end = i - 1; // 標記排好序陣列的尾部
            // 只要頭部一直小於尾部，說明temp還在2個標記範圍內
            while (begin <= end) {
                // 取2個標記的中間資料的值
                int mid = (begin + end) / 2;
                // 比較，若比中間值大，則範圍縮小一半
                if (temp > source[mid]) {
                    begin = mid + 1;
                    // 否則，範圍也是縮小一半
                } else {
                    end = mid - 1;
                }
                // 迴圈結束時，end<begin,即i應該插入到begin所在的索引
            }
            // 從begin到i，集體後移
            for (int j = i; j > begin; j--) {
                source[j] = source[j - 1];
            }
            // 插入i
            source[begin] = temp;
        }
        System.out.println("折半插入排序，花費時間(s):" + ((System.currentTimeMillis() - nowTime) / 1000.0) + "s");
    }
 

3.     shell排序

思路：

Shell排序也是對直接插入排序的改進。它實質上是一種分組插入方法。

下面希爾排序的步長選擇都是從n/2開始，每次再減半，直到最後為1。

時間複雜度 ： O(nlog2^n)

 /**
     * 希爾排序
     * 針對直接插入排序的下效率問題，有人對次進行了改進與升級，這就是現在的希爾排序。
     * 希爾排序，也稱遞減增量排序演算法，是插入排序的一種更高效的改進版本。希爾排序是非穩定排序演算法。
     * 首先確定分的組數。
     * 然後對組中元素進行插入排序。
     * 然後將length/2，重複1,2步，直到length=0為止。
     * @param arr
     */
    public void shellSort(int [] arr){
        long nowTime = System.currentTimeMillis();
        int len=arr.length;//單獨把陣列長度拿出來，提高效率
        while(len!=0){
            len=len/2;
            for(int i=0;i<len;i++){//分組
                for(int j=i+len;j<arr.length;j+=len){//元素從第二個開始
                    int k=j-len;//k為有序序列最後一位的位數
                    int temp=arr[j];//要插入的元素
                    /*for(;k>=0&&temp<arr[k];k-=len){
                        arr[k+len]=arr[k];
                    }*/
                    while(k>=0&&temp<arr[k]){//從後往前遍歷
                        arr[k+len]=arr[k];
                        k-=len;//向後移動len位
                    }
                    arr[k+len]=temp;
                }
            }
        }
        System.out.println("希爾排序，花費時間(s):" + ((System.currentTimeMillis() - nowTime) / 1000.0) + "s");
    }

耗時對比：

10W 條隨機 資料 執行如圖：

可以看出希爾排序時間明顯（比直插排序和折半排序）縮短。折半排序和直插排序時間差不多。

50W 條隨機 資料 執行如圖：

可以看出希爾排序時間明顯（比直插排序和折半排序）縮短。折半排序和直插排序時間差不多。

100W 條隨機 資料 執行如圖：

可以看出希爾排序時間明顯（比直插排序和折半排序）縮短。折半排序比直插排序耗時更多。

總結：

直接插入排序寫法比較簡單，平均時間複雜度為：O(n^2) 。

折半插入排序，平均時間複雜度為：O(n^2) 。

希爾排序，平均時間複雜度為：O(nlog2^n) 。

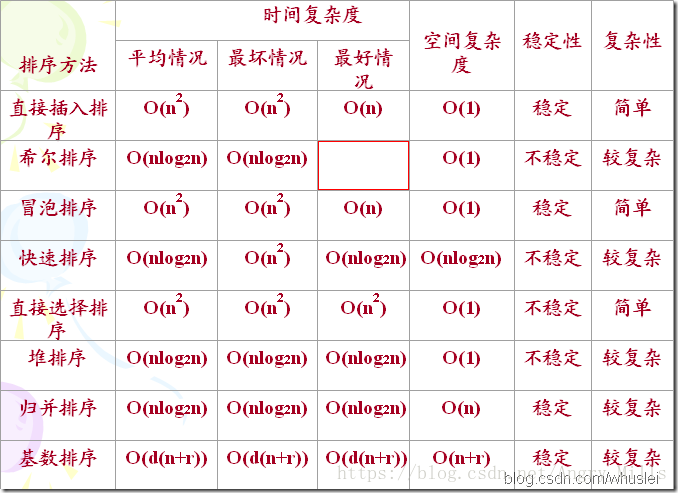
各種排序方法比較：

更多排序演算法：

氣泡排序   ：  https://blog.csdn.net/Angry_Mills/article/details/81057900