EFM (Explicit Factor Models)顯因子模型
阿新 • • 發佈：2018-12-27
SiGIR 2014在推薦系統方面收錄了三篇很有價值的論文，提出了新的演算法框架。在此介紹第一種演算法框架（來自論文：Explicit Factor Models for Explainable Recommendation based
on Phrase-level Sentiment Analysis，基於短語級情感分析的可解釋型推薦模型——顯因子模型）。如與本文有不同理解，不吝賜教。
一、概述
EFM ( Explicit Factor Models，顯因子模型），是針對LFM (Latent Factor Models，隱因子模型) 的不足而設計的。
LFM的特點如下：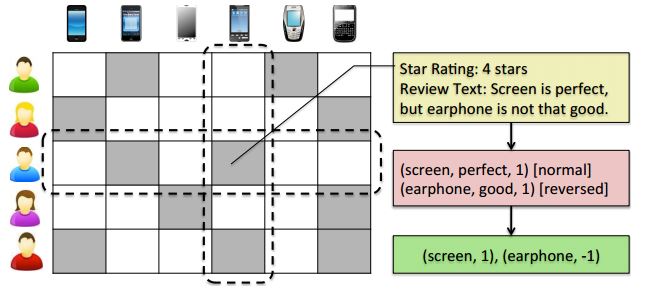 
首先，從使用者評論的語料庫抽取物品的特徵（或者說，物品的某一方面）：screen、earphone。然後，抽取使用者對這些特徵的意見：perfect、good。如果這些表示意見的詞彙本身是積極的情感，則用1表示；反之則用-1表示。所以在這個例子中，情感短語表示為（screen, perfect, 1）, （earphone, good, 1），這一條條短語就組成了情感詞典。 根據情感詞典，對使用者評論進行情感分析，判斷使用者的情感是肯定的還是否定的。例如：perfect是肯定的，而good是否定的，因為前面加了否定詞not。所以，這個例子中，使用者的評論就可以表示成特徵/情感對：（screen, 1）, （earphone, -1）。 把使用者的評論表示為特徵/情感對，是構建情感詞典的目的。 2. 構建矩陣 EFM需要構建三個矩陣。 第一個是使用者打分矩陣A，表示第 i 個使用者對第 j 個物品打的分數。由於使用者不一定對所有物品都打過分數，所以沒打分則記為零。 第二個是使用者-特徵關注矩陣X，表示第 i 個使用者對第 j 個特徵的喜好程度：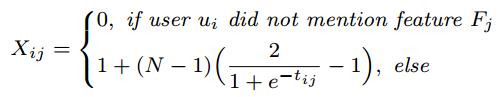
其中，N表示使用者打分的最高分數（一般為5分）。為了使該矩陣的每個值與使用者打分矩陣的值範圍都是[1, N]，用sigmoid函式規範引數的取值。
第三個是物品-特徵質量矩陣Y，表示第 i 個物品包含第 j 個特徵的程度：
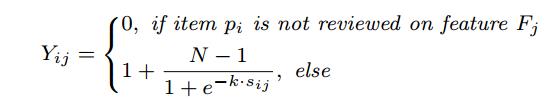
其中，k表示第 i 個物品的第 j 個特徵被使用者提到了幾次。k次提到則被表示成k個特徵/情感對，計算這k個對的取值（1或-1）的平均值，則為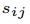
。
3. 估計矩陣X、Y、A的缺失值 矩陣X、Y中的非零數表示已有的使用者或物品與特徵之間的關係，而零則表示尚未清楚的缺失值。為了估計這些缺失值，則採用最優化損失函式的方法。 損失函式是把一個事件對映到能表示與其相關的經濟成本或機會成本的實數的一種函式。在統計學中，損失函式經常用來估計引數。損失函式的未知引數用 θ 表示，決策的方案（已獲得的實際值）用 d 表示，常見的損失函式有兩種： 二次損失函式： L(θ,d) = c(θ − d)2 絕對損失函式： L(θ,d) = c |θ − d| 該演算法採用的是二次損失函式。採用最優化損失函式的方法，是指最小化估計值與真實值的差距。所以X、Y的最優化損失函式如下：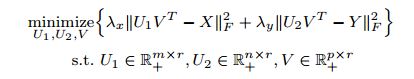
與LFM相比，EFM已經抽取出了顯式的特徵。我們假設一些特徵屬於某一型別，而使用者喜歡這一型別或者物品包含這一型別，由於特徵是顯式的，因而引入“顯因子”的概念。上面表示式中的 r 就是指顯因子的數量。
同理，估計打分矩陣A的缺失值也會用到顯因子。同時，考慮到使用者在打分時還會考慮到其他一些潛在的因素，因此也引入了LFM中用到的隱因子，用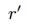
表示隱因子的數量。A的最優化損失函式為：
，
，
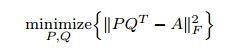
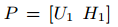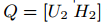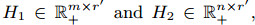
然後把這兩個損失函式合併為：
( * )
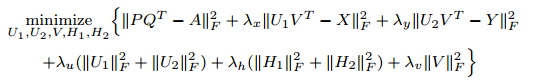其中，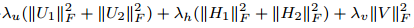
是防止過擬合的正則化項。
( * )式通過拉格朗日函式和KKT條件的推導後，得到矩陣V、U1、U2、H1、H2的更新公式，如下所示：
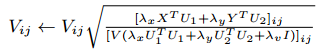
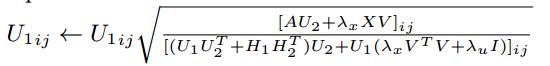
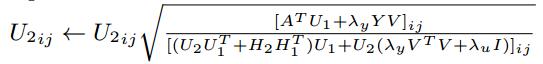
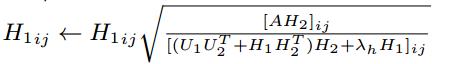
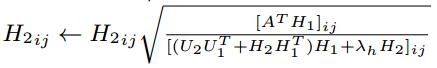
設定迭代次數進行迭代，或者在引數收斂後，得到以上5個矩陣的引數值，從而估計X、Y、A的缺失值：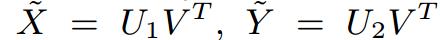
，
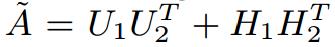4. Top-K推薦
向量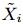
的行表示第
i 個使用者對每個特徵的喜好程度，選取其中引數值最大的k個特徵的下標，用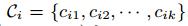
表示。然後用以下方法計算第
i 個使用者對第 j 個物品的打分：
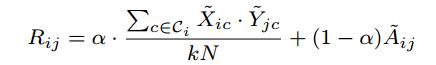
其中，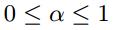
，具體的值由實驗確定。在大多數打分系統中，最高分數為5，所以N=5。
最後，選擇打分最高的前K個物品推薦給使用者，並根據特徵向用戶解釋推薦理由。
首先，從使用者評論的語料庫抽取物品的特徵（或者說，物品的某一方面）：screen、earphone。然後，抽取使用者對這些特徵的意見：perfect、good。如果這些表示意見的詞彙本身是積極的情感，則用1表示；反之則用-1表示。所以在這個例子中，情感短語表示為（screen, perfect, 1）, （earphone, good, 1），這一條條短語就組成了情感詞典。 根據情感詞典，對使用者評論進行情感分析，判斷使用者的情感是肯定的還是否定的。例如：perfect是肯定的，而good是否定的，因為前面加了否定詞not。所以，這個例子中，使用者的評論就可以表示成特徵/情感對：（screen, 1）, （earphone, -1）。 把使用者的評論表示為特徵/情感對，是構建情感詞典的目的。 2. 構建矩陣 EFM需要構建三個矩陣。 第一個是使用者打分矩陣A，表示第 i 個使用者對第 j 個物品打的分數。由於使用者不一定對所有物品都打過分數，所以沒打分則記為零。 第二個是使用者-特徵關注矩陣X，表示第 i 個使用者對第 j 個特徵的喜好程度：
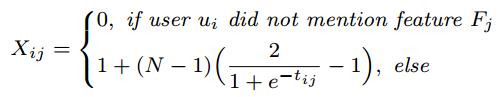其中，N表示使用者打分的最高分數（一般為5分）。為了使該矩陣的每個值與使用者打分矩陣的值範圍都是[1, N]，用sigmoid函式規範引數的取值。
第三個是物品-特徵質量矩陣Y，表示第 i 個物品包含第 j 個特徵的程度：
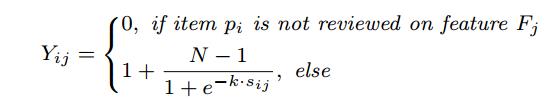
其中，k表示第 i 個物品的第 j 個特徵被使用者提到了幾次。k次提到則被表示成k個特徵/情感對，計算這k個對的取值（1或-1）的平均值，則為
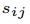。3. 估計矩陣X、Y、A的缺失值 矩陣X、Y中的非零數表示已有的使用者或物品與特徵之間的關係，而零則表示尚未清楚的缺失值。為了估計這些缺失值，則採用最優化損失函式的方法。 損失函式是把一個事件對映到能表示與其相關的經濟成本或機會成本的實數的一種函式。在統計學中，損失函式經常用來估計引數。損失函式的未知引數用 θ 表示，決策的方案（已獲得的實際值）用 d 表示，常見的損失函式有兩種： 二次損失函式： L(θ,d) = c(θ − d)2 絕對損失函式： L(θ,d) = c |θ − d| 該演算法採用的是二次損失函式。採用最優化損失函式的方法，是指最小化估計值與真實值的差距。所以X、Y的最優化損失函式如下：
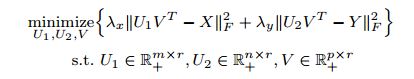與LFM相比，EFM已經抽取出了顯式的特徵。我們假設一些特徵屬於某一型別，而使用者喜歡這一型別或者物品包含這一型別，由於特徵是顯式的，因而引入“顯因子”的概念。上面表示式中的 r 就是指顯因子的數量。
同理，估計打分矩陣A的缺失值也會用到顯因子。同時，考慮到使用者在打分時還會考慮到其他一些潛在的因素，因此也引入了LFM中用到的隱因子，用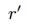表示隱因子的數量。A的最優化損失函式為：
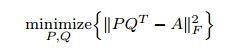
，，然後把這兩個損失函式合併為：
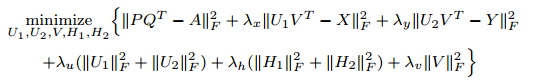( * )其中，
是防止過擬合的正則化項。
( * )式通過拉格朗日函式和KKT條件的推導後，得到矩陣V、U1、U2、H1、H2的更新公式，如下所示：
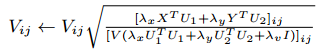
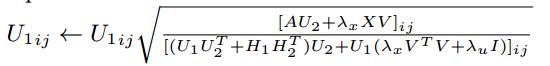
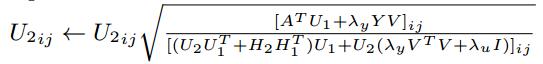
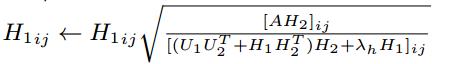
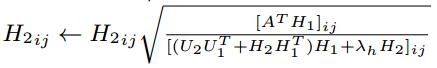
設定迭代次數進行迭代，或者在引數收斂後，得到以上5個矩陣的引數值，從而估計X、Y、A的缺失值：
，
4. Top-K推薦
向量的行表示第
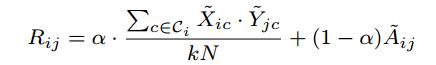
i 個使用者對每個特徵的喜好程度，選取其中引數值最大的k個特徵的下標，用表示。然後用以下方法計算第
i 個使用者對第 j 個物品的打分：
其中，
，具體的值由實驗確定。在大多數打分系統中，最高分數為5，所以N=5。
最後，選擇打分最高的前K個物品推薦給使用者，並根據特徵向用戶解釋推薦理由。