誒，演算法這個東西，其實沒那麼簡單，但是也沒那麼難。

紅黑樹，其實已經有很多大佬都整理過了，而且文章部落格都寫得超好，我寫這篇文章的目的是：自己整理一次，這些知識才是自己的，否則永遠是別人的~

該系列到現在暫只有3篇文章：

【演算法】紅黑樹（二叉樹）概念與查詢（一）：https://blog.csdn.net/lsr40/article/details/85230703

【演算法】紅黑樹插入資料（變色，左旋、右旋）（二）：https://blog.csdn.net/lsr40/article/details/85245027

【演算法】紅黑樹插入資料的情況與實現（三）：https://blog.csdn.net/lsr40/article/details/85266069

本文先講講概念和查詢！

本人菜雞，如果文中有誤，還請各位批評指出！！！一定加以改正（雖然可能會解釋得不清楚，但是絕對不能誤導新人）！

關於資料儲存結構，無非就是增刪改查（資料庫不就是這樣），對於紅黑樹來說改不就相當於把原來的值remove（刪除），然後再put（插入/新增）一個新的值，所以主要還是瞭解增刪查！

一、概念

1、類似紅黑樹的這種樹狀結構有什麼用？

可以用來快速解決一些查詢問題，大家請看圖

二叉樹基本性質：二叉樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”（left subtree）和“右子樹”（right subtree）。

用自己的話總結下：

1、有一個根節點

2、每個節點都有兩個分支

3、最下面的節點叫葉子節點

所以如果把資料變成二叉樹就可以直接看到最左邊的葉子節點是最小值，最右邊的葉子節點是最大值，而且我們在遍歷的時候，我只需要遍歷3次就可以找到我想要的值！

2、相同的資料可以構成很多顆二叉樹啊，哪種是最好的，哪種是最壞的？

如下兩圖

獲得最大值和最小值的遍歷次數，似乎變多了？而且整個二叉樹的高度變高了，但是這兩張圖，好像也沒有違反二叉樹的任何規則，所以我們發現如果二叉樹偏向嚴重的話，會導致效率變低，當全部偏成一條的時候，效率是最差的，大概如圖：

所以除了最後一層樹枝上（總體的最後一層是葉子，所以最後一層樹枝就是總體的倒數第二層），可以不用都存在左右節點，其他的樹枝上最好都存在左右子節點，也就是不偏的二叉樹，效率會比偏的二叉樹效率高！（合理的高度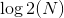

3、我聽說過什麼用中序，前序，後序遍歷二叉樹是幹嘛的？

這裡就不再介紹中序，前序，後序是如何遍歷的了，就直接說應用在哪裡！

-1.前序遍歷：可以用來實現目錄結構的顯示。

-2.中序遍歷：一顆樹，被中序遍歷之後，就是value從小到大的排列，當然也可以用來做表示式樹，在編譯器底層實現的時候使用者可以實現基本的加減乘除，比如 a*b+c。

-3.後序遍歷：可以用來實現計算目錄內的檔案佔用的資料大小。

4、紅黑樹和二叉樹又有什麼區別？

紅黑樹是一種特殊的二叉樹！

我們也發現，相同資料生成的二叉樹形狀各異，有些效能好，有些效能差，紅黑樹是一種自平衡二叉樹，就是在每次插入新的資料的時候，紅黑樹會進行變色和旋轉來使生成的樹不會出現偏的情況

（1）每個節點或者是黑色，或者是紅色。

（2）根節點是黑色。

（3）每個葉子節點（NIL）是黑色。 [注意：這裡葉子節點，是指為空(NIL或NULL)的葉子節點！]

（4）如果一個節點是紅色的，則它的子節點必須是黑色的，也就是說不可能出現兩個連續的紅色節點，不過兩個連續的黑色節點是可能出現的

（5）從任意一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。

後兩條特性才是最關鍵的！

當然，如果您覺得我的翻譯不夠準確的話，可以看看英文原文

（1）Each node is either red or black.

（2）The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black,but not necessarily vice versa, this rule has little effect on analysis.

（3）All leaves (NIL) are black.

（4）If a node is red, then both its children are black.

（5）Every path from a given node to any of its descendant NIL nodes contains the same number of black nodes.

英文wiki地址：https://en.wikipedia.org/wiki/Red%E2%80%93black_tree

二、查詢

紅黑樹的查詢和普通的二叉樹查詢是一樣的，當我想查某個數的時候，只需要把這個數從根節點比較，如果比根節點大，那就繼續比較根節點的右節點，否則就是根節點的左節點，以此類推。

java中的TreeMap底層就是實現紅黑樹。

一起來看看java是怎麼實現的？

 //在TreeMap的277行，get方法
 public V get(Object key) {
		//通過getEntry方法，獲得對應的p點
        Entry<K,V> p = getEntry(key);
        return (p==null ? null : p.value);
    }

 //在342行getEntry方法
 final Entry<K,V> getEntry(Object key) {
        // Offload comparator-based version for sake of performance
        if (comparator != null)
            return getEntryUsingComparator(key);
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
		//將傳入的key，變成一個可比較的型別，賦值為k
            Comparable<? super K> k = (Comparable<? super K>) key;
		//前面的判斷是獲得比較器，然後獲得root也就是根節點p
        Entry<K,V> p = root;
		//進入迴圈，一直到p為空才停止
        while (p != null) {
            int cmp = k.compareTo(p.key);
			//如果傳入的key比根節點小，p重新賦值，p變為該節點的左節點
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
			//如果傳入的key比根節點大，p重新賦值，p變為該節點的右節點
                p = p.right;
            else
			//如果不大於也不小於，證明找到該值，就將該值return
                return p;
        }
		//如果遍歷結束，都沒有進入到 return p，證明傳入的key不存在，直接返回null
        return null;
    }

所以查詢是最簡單的，只要是二叉樹，都是這種查詢方式！

那麼本篇的內容也說完了。

總結：

1、二叉樹是什麼，有什麼用？

簡答：將N個數據插入到一顆二叉樹中，來減少迭代的次數，加快查詢

2、二叉樹中的前序，中序，後序遍歷是什麼？

簡答：按照一定的順序遍歷二叉樹，各有各的應用場景

3、紅黑樹又是什麼，它有哪些性質，為什麼會有紅黑樹出現？

簡答：二叉樹有可能會偏，導致查詢效能不能達到理想的優化，紅黑樹是自平衡二叉樹，每次插入新的資料的時候，會變色和旋轉，來讓高度保持在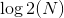這個合理高度內

4、java中treemap是如何實現紅黑樹的查詢的？

簡答：如程式碼所示

5、分享一個生成紅黑樹的網站！

http://sandbox.runjs.cn/show/2nngvn8w

好了，本人菜雞一隻，也在繼續學習中，接下來會更新紅黑樹的插入（紅黑樹的刪除我可能也會更吧，但是其實我現在也還沒搞太明白，希望過段時間能清晰的搞懂），如果我有什麼筆誤的地方，還望大家批評指出，儘量做到不誤導新人！有什麼問題，大家也可以留言討論~