TensorFlow HOWTO 4.1 多層感知機(分類)
阿新 • • 發佈:2018-12-28
4.1 多層感知機(分類)
這篇文章開始就是深度學習了。多層感知機的架構是這樣:
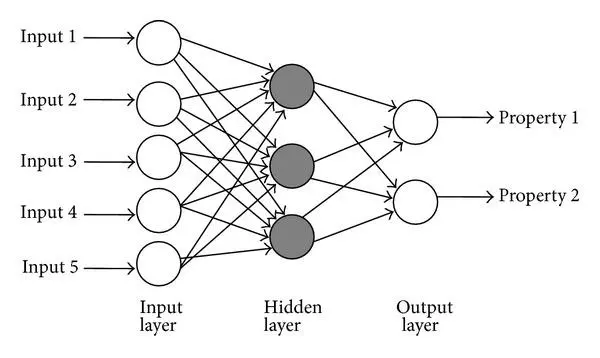
輸入層除了提供資料之外,不幹任何事情。隱層和輸出層的每個節點都計算一次線性變換,並應用非線性啟用函式。隱層的啟用函式是壓縮性質的函式。輸出層的啟用函式取決於標籤的取值範圍。
其本質上相當於廣義線性迴歸模型的整合。
操作步驟
匯入所需的包。
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import sklearn.datasets as 匯入資料,並進行預處理。我們使用鳶尾花資料集所有樣本。根據萼片長度和花瓣長度預測樣本是不是雜色鳶尾(第二種)。要注意雜色鳶尾在另外兩種之間,所以它不是線性問題。
iris = ds.load_iris()
x_ = iris.data[:, [0, 2]]
y_ = (iris.target == 1).astype(int)
y_ = np.expand_dims(y_ , 1)
x_train, x_test, y_train, y_test = \
ms.train_test_split( 定義超引數。
| 變數 | 含義 |
|---|---|
n_input |
樣本特徵數 |
n_epoch |
迭代數 |
n_hidden1 |
隱層 1 的單元數 |
n_hidden2 |
隱層 2 的單元數 |
lr |
學習率 |
threshold |
如果輸出超過這個概率,將樣本判定為正樣本 |
n_input = 2
n_hidden1 = 4
n_hidden2 = 4
n_epoch = 2000
lr = 0.05
threshold = 0.5
搭建模型。要注意隱層的啟用函式使用了目前暫時最優的 ELU。由於這個是二分類問題,輸出層啟用函式只能是 Sigmoid。
| 變數 | 含義 |
|---|---|
x |
輸入 |
y |
真實標籤 |
w_l{1,2,3} |
第{1,2,3}層的權重 |
b_l{1,2,3} |
第{1,2,3}層的偏置 |
z_l{1,2,3} |
第{1,2,3}層的中間變數,前一層輸出的線性變換 |
a_l{1,2,3} |
第{1,2,3}層的輸出,其中a_l3樣本是正樣本的概率 |
x = tf.placeholder(tf.float64, [None, n_input])
y = tf.placeholder(tf.float64, [None, 1])
w_l1 = tf.Variable(np.random.rand(n_input, n_hidden1))
b_l1 = tf.Variable(np.random.rand(1, n_hidden1))
w_l2 = tf.Variable(np.random.rand(n_hidden1, n_hidden2))
b_l2 = tf.Variable(np.random.rand(1, n_hidden2))
w_l3 = tf.Variable(np.random.rand(n_hidden2, 1))
b_l3 = tf.Variable(np.random.rand(1, 1))
z_l1 = x @ w_l1 + b_l1
a_l1 = tf.nn.elu(z_l1)
z_l2 = a_l1 @ w_l2 + b_l2
a_l2 = tf.nn.elu(z_l2)
z_l3 = a_l2 @ w_l3 + b_l3
a_l3 = tf.sigmoid(z_l3)
定義交叉熵損失、優化操作、和準確率度量指標。
| 變數 | 含義 |
|---|---|
loss |
損失 |
op |
優化操作 |
y_hat |
標籤的預測值 |
acc |
準確率 |
loss = - tf.reduce_mean(y * tf.log(a_l3) + (1 - y) * tf.log(1 - a_l3))
op = tf.train.AdamOptimizer(lr).minimize(loss)
y_hat = tf.to_double(a_l3 > threshold)
acc = tf.reduce_mean(tf.to_double(tf.equal(y_hat, y)))
使用訓練集訓練模型。
losses = []
accs = []
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(n_epoch):
_, loss_ = sess.run([op, loss], feed_dict={x: x_train, y: y_train})
losses.append(loss_)
使用測試集計算準確率。
acc_ = sess.run(acc, feed_dict={x: x_test, y: y_test})
accs.append(acc_)
每一百步列印損失和度量值。
if e % 100 == 0:
print(f'epoch: {e}, loss: {loss_}, acc: {acc_}')
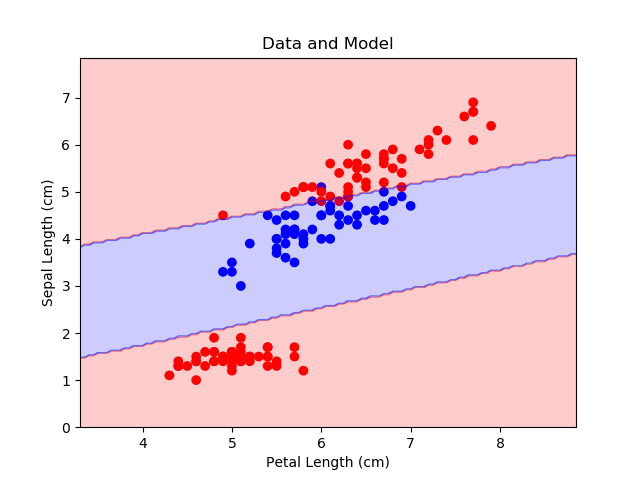
得到決策邊界:
x_plt = x_[:, 0]
y_plt = x_[:, 1]
c_plt = y_.ravel()
x_min = x_plt.min() - 1
x_max = x_plt.max() + 1
y_min = y_plt.min() - 1
y_max = y_plt.max() + 1
x_rng = np.arange(x_min, x_max, 0.05)
y_rng = np.arange(y_min, y_max, 0.05)
x_rng, y_rng = np.meshgrid(x_rng, y_rng)
model_input = np.asarray([x_rng.ravel(), y_rng.ravel()]).T
model_output = sess.run(y_hat, feed_dict={x: model_input}).astype(int)
c_rng = model_output.reshape(x_rng.shape)
輸出:
epoch: 0, loss: 8.951598255929909, acc: 0.28888888888888886
epoch: 100, loss: 0.5002945631529941, acc: 0.7333333333333333
epoch: 200, loss: 0.10712651780120697, acc: 0.9333333333333333
epoch: 300, loss: 0.08321807852608396, acc: 0.9333333333333333
epoch: 400, loss: 0.08013835031876741, acc: 0.9333333333333333
epoch: 500, loss: 0.07905186419367002, acc: 0.9333333333333333
epoch: 600, loss: 0.07850865683940819, acc: 0.9333333333333333
epoch: 700, loss: 0.07808251016428093, acc: 0.9333333333333333
epoch: 800, loss: 0.07780712763974691, acc: 0.9333333333333333
epoch: 900, loss: 0.07759866398922599, acc: 0.9333333333333333
epoch: 1000, loss: 0.07744327666591566, acc: 0.9333333333333333
epoch: 1100, loss: 0.07731295774932465, acc: 0.9333333333333333
epoch: 1200, loss: 0.07721162022836371, acc: 0.9333333333333333
epoch: 1300, loss: 0.07712807776857629, acc: 0.9333333333333333
epoch: 1400, loss: 0.07735547120278226, acc: 0.9333333333333333
epoch: 1500, loss: 0.07700215794853897, acc: 0.9333333333333333
epoch: 1600, loss: 0.07695230759382654, acc: 0.9333333333333333
epoch: 1700, loss: 0.07690933782097598, acc: 0.9333333333333333
epoch: 1800, loss: 0.07687191279304387, acc: 0.9333333333333333
epoch: 1900, loss: 0.07683911419647445, acc: 0.9333333333333333
繪製整個資料集以及決策邊界。
plt.figure()
cmap = mpl.colors.ListedColormap(['r', 'b'])
plt.scatter(x_plt, y_plt, c=c_plt, cmap=cmap)
plt.contourf(x_rng, y_rng, c_rng, alpha=0.2, linewidth=5, cmap=cmap)
plt.title('Data and Model')
plt.xlabel('Petal Length (cm)')
plt.ylabel('Sepal Length (cm)')
plt.show()
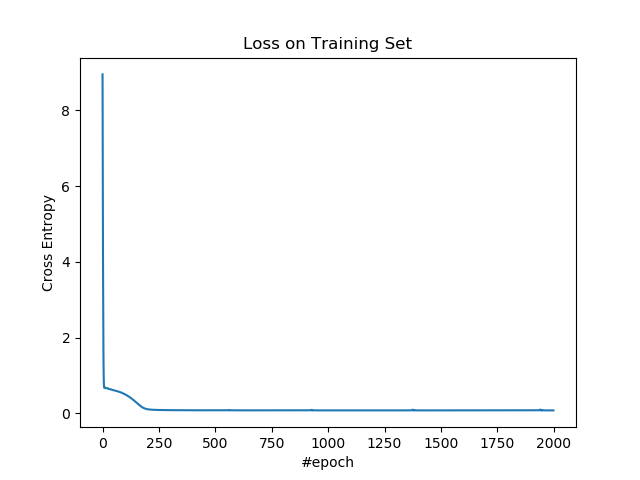
繪製訓練集上的損失。
plt.figure()
plt.plot(losses)
plt.title('Loss on Training Set')
plt.xlabel('#epoch')
plt.ylabel('Cross Entropy')
plt.show()
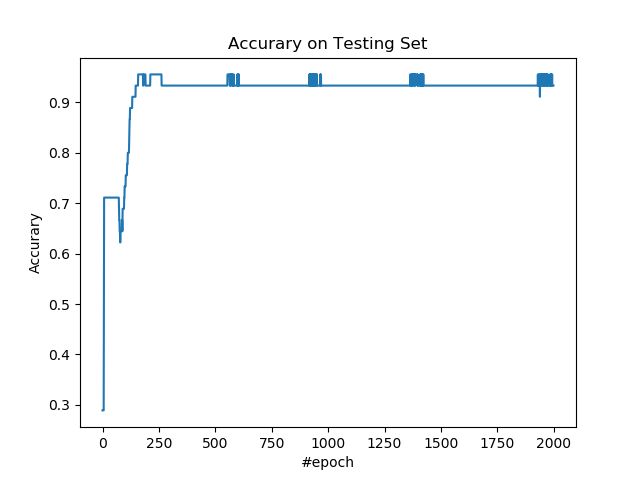
繪製測試集上的準確率。
plt.figure()
plt.plot(accs)
plt.title('Accurary on Testing Set')
plt.xlabel('#epoch')
plt.ylabel('Accurary')
plt.show()