Weapons of Micro Destruction: How Our ‘Likes’ Hijacked Democracy
In the 1st half of the equation, measure of fit, we have a simple mean squared error equation (the 1/2 term in front is there to simplify the math that we’ll explore in part 5).
In the 2nd half of the equation, L1 penalty, if lambda (a tuning parameter we control) is greater than zero, then adding the absolute
Thus, the ‘Least Absolute Shrinkage’ or ‘LAS’ in LASSO.
Think of the L1 penalty as a shrink ray. It will shrink the size of the coefficients…and it could potentially make the coefficient disappear.

You may be wondering why we would want to add a penalty at all to shrink the size of our coefficients? The answer is to prevent “over fitting.”
Over fitting occurs when the algorithm “memorizes the training data” and means it won’t generalize well against unseen/test data. Adding the penalty helps “regularize” the magnitude of the coefficients and improves the algorithm’s predictions on the holdout data it’s never seen.

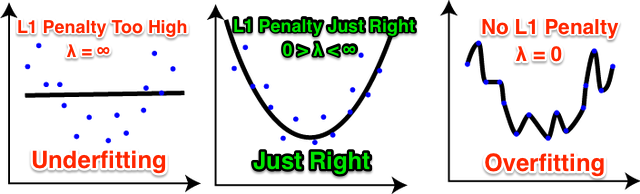
As we’ll see in the next section, when the lambda value is high enough, it also forces some coefficients to zero and therefore acts as a ‘selection operator’ (the ‘SO’ in LASSO). A page with a zero coefficient means the page is ignored in the prediction and when we have many pages with zero coefficients, this is referred to as a “sparse solution.”
Conversely, if the coefficient is large (really high or really low), it means the page has a high degree of influence.
4.3 How to Choose Lambda in LASSO Regression
A popular technique for choosing the best lambda value is called cross-validation.
In k-fold cross-validation, you arbitrarily choose a series of lambdas (I use 0.0, 0.01, 0.10, 1.0 in the Excel model), see how each performs on your validation sets, and choose the lambda that has the lowest average error across all validation sets.
For instance, if we had enough data (not shown in Excel), we would split up our data into training/test sets and then further split up our training data into 5 (k) folds or partitions. After testing each lambda on the 5 validation sets, we’d choose the one which resulted in the lowest average error.
