The Nature of Infinity

Sometimes I think of infinity (∞) as being the furthest number from zero (0) on a number line but that’s not right. Zero is an even integer, while infinity is nothing of the sort. Infinity isn’t a number like zero or even a googol. Infinity is more of a concept than anything else. It simply describes something larger than any natural number. When you think about it, there are numbers so big that they don’t even have names yet and they are still much less than infinity. The whole point is that the number line simply never ends. You can always just add one more, and that’s what infinity really is. Infinity is merely the idea of endlessness, of going on forever. This is why it’s technically a concept and not a number. Of course, if we’re really being technical then I guess I would have to say, if infinity were truly limitless then it wouldn’t even be nameable.

Regardless, although Ancient pre-socratic Greeks like Anaximander spoke of the idea of limitlessness philosophically, it seems to have been Zeno of Elea who first mathematically codified infinity in the 5th century BCE. Aristotle understood that you could just start counting off the numbers one by one and keep doing it until you die. Someone else could even continue where you left off but someday the world would end and it would all have to stop. So people can theoretically but not actually keep counting all of the numbers forever. Nonetheless, Archimedes later went on to define infinity with infinitely large sets using precise mathematical proofs. At the same time, there were very influential Ancient Indian Jainist mathematicians who classified numbers into three sets. These were enumerable, innumerable, and infinite. They also had two basic types of infinite numbers, between rigidly bounded and loosely bounded infinities. So, although Pythagoras was absolutely terrified of infinity, Mahavira was instrumental in the development of the idea.

Infinity really became a popular concept in 17th century Europe. In 1655 John Wallis first used the standard symbolic notation ∞ to represent a sort of numberless number. Then, in 1699 Sir Isaac Newton wrote about equations with an infinite number of terms. He and Gottfried Leibniz also co-invented infinitesimal calculus. Centuries later, Georg Cantor became insanely influential in the development of infinity. He took the concept to a whole new level in the 19th and 20th centuries, driving himself crazy thinking about numbers, defining infinite sets and even proving the existence of an “infinity of infinities”. Ultimately, Cantor showed that there are infinitely many possible sizes for infinite sets thus establishing “set theory” which became foundational in modern mathematics. In contemporary schools of thought, there are two kinds of infinity, “countable” and “uncountable”. Cantor also showed that infinities even come in different sizes. For instance, the infinite list of whole numbers is only half the size of the infinite list of integers, but they both contain the same number of elements, which is to say an infinite amount.

(1, 2, 3, 4, 5,…)

(0, 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, …)

It’s crazy. The lists get out of hand really quick too. For instance, think about trying to compile a list of all the decimals. How would you really even do that? To simplify the thought experiment, just think of a simple grid like this:

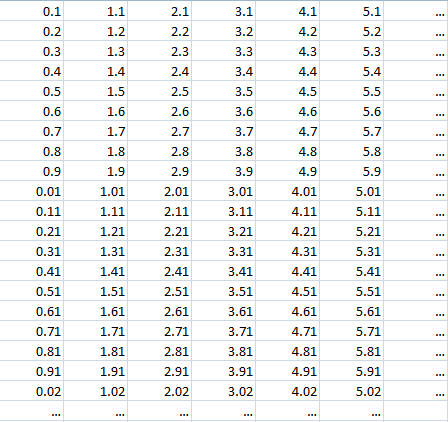
Problems arise from this immediately. For one thing, imagine just counting out all the decimal numbers. One issue even with the simple grid is that the first column would never end to start the second column, so it could only appear in rows but never be written out straight through. That is to say, zero-point-whatever (0.?) would never get to one-point-one (1.1). The columns and rows are both endless. So, how could it? The issue here is that there are infinite numbers between 0 and 1, like 0.12, 0.112, 0.1112, etc... To further complicate this, the decimal representation of the number pi starts with 3.14159, but no finite number of digits can represent π exactly, nor does Archimede’s constant ever repeat. This makes it impossible to write out pi entirely.

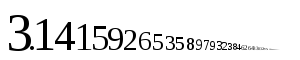
It’s easy enough to disprove the conjecture that it’s possible to list out every decimal number. Regardless of whatever list one might compile there will always be a new decimal number that could be made that isn’t on the list. The reality is that there is simply no way to list every decimal number. One can always construct a new decimal number that is not on the list by using the list and a simple algorithm:

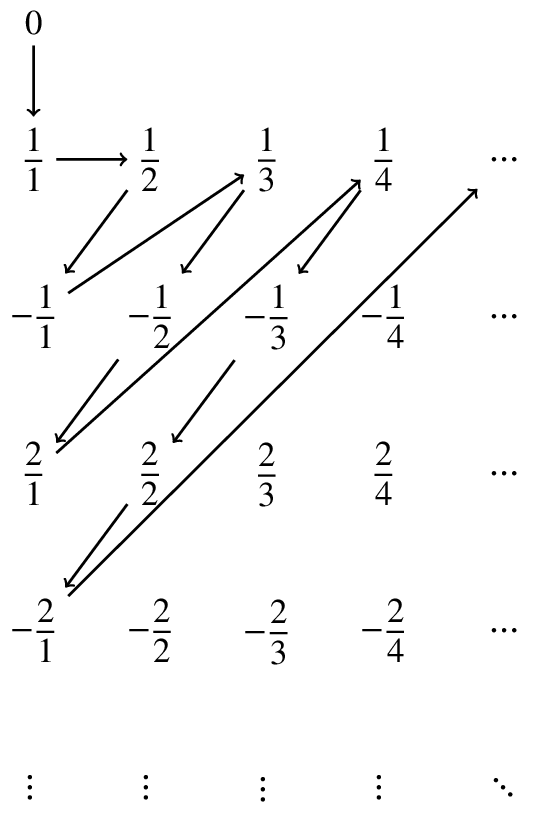
To implement Cantor’s clever proof by contradiction put the number in the first decimal place of the first number on the list in the digit in the first place of the number that’s not on the list. The second decimal comes from the second place of the second number and so on and so forth to produce a new number (0.4218…). The number that’s not on the list can’t be the first number because of the first decimal from the first number on the list, and so on. The irrational decimal numbers are truly “uncountable”, hence the distinction between those and the countable sets, like that of the fractions. Ultimately, the infinity of decimals is greater than the infinity of fractions, but we can never know by how much. To make matters worse, there is an infinite number of infinities of different sizes. Still, unlike decimals which can be infinitely long, rational fractions are countable numbers. To make a list of fractional numbers one can put them in a grid. So, just to simplify for clarity, in this way 2/5 would be found in the second row and the fifth column, and so on and so forth:

Of course, to count all the fractions one would need to begin with 1/1, and proceed in the following way:

Now, as if all this wasn’t mindblowing enough on its own, along with counting the infinite set of fractions, Georg Cantor conjectured in the “Continuum Hypothesis” (CH) that when it comes to numbers there is no size of infinity between the rational and real. He claimed that there isn’t limitlessness in between the rational integers and the real numbers. The former includes numbers like 4 and 56,789, while the latter includes 4/3, √2, and -10. To be more precise, according to CH:

There is no set whose cardinality is strictly between that of the integers and the real numbers.

Unfortunately, discovering all of this and then being ridiculed about it took a tremendous toll on Cantor. After years of struggling with bouts of depression, he eventually died in a sanatorium in 1918. They claimed the master mathematician was a madman, but they were wrong. Cantor was an absolute genius! The funny thing is that in the 1920’s, Kurt Godel demonstrated that it is impossible to prove that Cantor’s continuum hypothesis is false. Then in the 1960’s, Paul Cohen showed that it is impossible to prove that it is true. However, this hasn’t stopped the set theorist Hugh Woodin from searching for a solution beyond true or false. Who knows? Maybe a hypothesis can be something more than just tenable or untenable. The thing is that unless we somehow find out, that known unknown will continue proving to be an unanswerable question in mathematics forever. Such is the enigmatic, yet ever so elegant nature of infinity.