2. 程式人生 > >線段樹模板題5題

線段樹模板題5題

阿新 • • 發佈：2018-12-29

題目描述

如題，已知一個數列，你需要進行下面兩種操作：

1.將某區間每一個數加上x

2.求出某區間每一個數的和

輸入輸出格式

輸入格式：

 

第一行包含兩個整數N、M，分別表示該數列數字的個數和操作的總個數。

第二行包含N個用空格分隔的整數，其中第i個數字表示數列第i項的初始值。

接下來M行每行包含3或4個整數，表示一個操作，具體如下：

操作1： 格式：1 x y k 含義：將區間[x,y]內每個數加上k

操作2： 格式：2 x y 含義：輸出區間[x,y]內每個數的和

 

輸出格式：

 

輸出包含若干行整數，即為所有操作2的結果。

 

輸入輸出樣例

輸入樣例#1： 複製

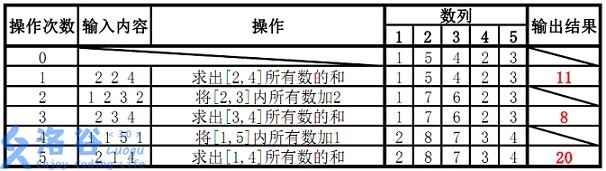
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

輸出樣例#1： 複製

11
8
20

說明

時空限制：1000ms,128M

資料規模：

對於30%的資料：N<=8，M<=10

對於70%的資料：N<=1000，M<=10000

對於100%的資料：N<=100000，M<=100000

（資料已經過加強^_^，保證在int64/long long資料範圍內）

樣例說明：

 

#include<iostream>
using namespace std;
const int maxn = 100010;
int n, m, p, x, a, b;
long long ans;
struct Node {
    long long l, r, w, f;
}node[4 * maxn + 10];

void build(int l, int r, int k) {
    node[k].r = r;
    node[k].l = l;
    if (l == r) {
        cin >> node[k].w;
        return;
    }
    int mid = (r + l) / 2;
    build(l, mid, k * 2);
    build(mid + 1, r, k * 2 + 1);
    node[k].w = node[k * 2].w + node[k * 2 + 1].w;
}

void down(int k) {
    node[k * 2].f += node[k].f;
    node[k * 2 + 1].f += node[k].f;
    node[k * 2].w += (node[k * 2].r - node[k * 2].l + 1) * node[k].f;
    node[k * 2 + 1].w += (node[k * 2 + 1].r - node[k * 2 + 1].l + 1) * node[k].f;
    node[k].f = 0;
}

void add(int k) {
    if (node[k].l >= a && node[k].r <= b) {
        node[k].w += (node[k].r -node[k].l + 1) * x;
        node[k].f += x;
        return;
    }
    if (node[k].f) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        add(k * 2);
    }
    if (b > mid) {
        add(k * 2 + 1);
    }
    node[k].w = node[k * 2].w + node[k * 2 + 1].w;
}

void sum(int k) {
    if (node[k].l >= a && node[k].r <= b) {
        ans += node[k].w;
        return;
    }
    if (node[k].f) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        sum(k * 2);
    }
    if (b > mid) {
        sum(k * 2 + 1);
    }
}

int main () {
    cin >> n >> m;
    build(1, n, 1);
    for (int i = 1; i <= m; i++) {
        cin >> p;
        ans = 0;
        if (p == 1) {
            cin >> a >> b >> x;
            add(1);
        } else {
            cin >> a >> b;
            sum(1);
            cout << ans << endl;
        }
    }
    return 0;
}

 

 

題目描述

如題，已知一個數列，你需要進行下面三種操作：

1.將某區間每一個數乘上x

2.將某區間每一個數加上x

3.求出某區間每一個數的和

輸入輸出格式

輸入格式：

 

第一行包含三個整數N、M、P，分別表示該數列數字的個數、操作的總個數和模數。

第二行包含N個用空格分隔的整數，其中第i個數字表示數列第i項的初始值。

接下來M行每行包含3或4個整數，表示一個操作，具體如下：

操作1： 格式：1 x y k 含義：將區間[x,y]內每個數乘上k

操作2： 格式：2 x y k 含義：將區間[x,y]內每個數加上k

操作3： 格式：3 x y 含義：輸出區間[x,y]內每個數的和對P取模所得的結果

 

輸出格式：

 

輸出包含若干行整數，即為所有操作3的結果。

 

輸入輸出樣例

輸入樣例#1： 複製

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

輸出樣例#1： 複製

17
2

說明

時空限制：1000ms,128M

資料規模：

對於30%的資料：N<=8，M<=10

對於70%的資料：N<=1000，M<=10000

對於100%的資料：N<=100000，M<=100000

（資料已經過加強^_^）

樣例說明：

故輸出應為17、2（40 mod 38=2）

 

思路：該題比較複雜，因為存在倆個不同的改變區域的方案，因此我設計了倆個懶標籤，同時因為要取模，所以有倆種方案的優先順序可以選擇，一種是先加後乘，另外一種是先乘後加，都是用在更新結點上，如果我們採取前者的方案可能存在精度損失，所以我們選擇後者，其他的具體看程式碼，注意down裡面的程式碼和一個懶標記很不一樣，其他也有一些部分需要稍微改改，總的來說這個題目真的是一個很不錯的模板題

#include<iostream>
using namespace std;
const int maxn = 100010;
struct Node{
    long long l, r, w, add, mul;
}node[4 * maxn + 10];

long long a, b, x, n, m, z, p, ans;
void build(int l, int r, int k) {
    node[k].r = r;
    node[k].l = l;
    node[k].mul = 1;
    if (l == r) {
        cin >> node[k].w;
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, k * 2);
    build(mid + 1, r, k * 2 + 1);
    node[k].w = (node[k * 2].w + node[k * 2 + 1].w) % p;
}

void down(int k) {
    node[k * 2].w = (node[k].mul * node[k * 2].w + node[k].add * (node[k * 2].r - node[k * 2].l + 1)) % p;
    node[k * 2 + 1].w = (node[k].mul * node[k * 2 + 1].w + node[k].add * (node[k * 2 + 1].r - node[k * 2 + 1].l + 1)) % p;
    node[k * 2].mul = (node[k].mul * node[k * 2].mul) % p;
    node[k * 2 + 1].mul = (node[k].mul * node[k * 2 + 1].mul) % p;
    node[k * 2].add = (node[k].mul * node[k * 2].add + node[k].add) % p;
    node[k * 2 + 1].add = (node[k].mul * node[k * 2 + 1].add + node[k].add) % p;
    node[k].mul = 1;
    node[k].add = 0;
}

void add(int k) {
    if (a <= node[k].l && b >= node[k].r) {
        node[k].w = (node[k].w + (node[k].r - node[k].l + 1) * x) % p;
        node[k].add = (node[k].add + x) % p;
        return;
    }
    if(node[k].add || node[k].mul != 1) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        add(k * 2);
    }
    if (b > mid) {
        add(k * 2 + 1);
    }
    node[k].w = (node[k * 2].w + node[k * 2 + 1].w) % p;
}

void mul(int k) {
    if (a <= node[k].l && b >= node[k].r) {
        node[k].w = (node[k].w * x) % p;
        node[k].mul = (node[k].mul * x) % p;
        node[k].add = (x * node[k].add) % p;
        return;
    }
    if(node[k].add || node[k].mul != 1) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        mul(k * 2);
    }
    if (b > mid) {
        mul(k * 2 + 1);
    }
    node[k].w = (node[k * 2].w + node[k * 2 + 1].w) % p;
}

void sum(int k) {
    if (a <= node[k].l && b >= node[k].r) {
        ans = (node[k].w + ans) % p;
        return;
    }
    if(node[k].add || node[k].mul != 1) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        sum(k * 2);
    }
    if (b > mid) {
        sum(k * 2 + 1);
    }
}


int main() {
    cin >> n >> m >> p;
    build(1, n, 1);
    for (int i = 1; i <= m; i++) {
        cin >> z;
        if (z == 1) {
            cin >> a >> b >> x;
            mul(1);
        } else if (z == 2) {
            cin >> a >> b >> x;
            add(1);
        } else {
            cin >> a >> b;
            ans = 0;
            sum(1);
            cout << ans << endl;
        }
    }
    return 0;
}

 

 

一行N個方格，開始每個格子裡都有一個整數。現在動態地提出一些問題和修改：提問的形式是求某一個特定的子區間[a,b]中所有元素的和；修改的規則是指定某一個格子x，加上或者減去一個特定的值A。現在要求你能對每個提問作出正確的回答。1≤N<100000，,提問和修改的總數m<10000條。

輸入描述 Input Description

輸入檔案第一行為一個整數N，接下來是n行n個整數，表示格子中原來的整數。接下一個正整數m，再接下來有m行，表示m個詢問，第一個整數表示詢問代號，詢問代號1表示增加，後面的兩個數x和A表示給位置X上的數值增加A，詢問代號2表示區間求和，後面兩個整數表示a和b，表示要求[a,b]之間的區間和。

輸出描述 Output Description

共m行，每個整數

樣例輸入 Sample Input

6

4 

5 

6 

2 

1 

3

4

1 3 5

2 1 4

1 1 9

2 2 6

樣例輸出 Sample Output

22

22

資料範圍及提示 Data Size & Hint

1≤N≤100000， m≤10000 。

#include<iostream>
using namespace std;
const int maxn = 100000;
int n, x, y, p, ans, m;
struct node {
    int l, r, w;
}tree[4 * maxn + 10];

void build(int l, int r, int k) {
    tree[k].l = l;
    tree[k].r = r;
    if (l == r) {
        cin >> tree[k].w;
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, k * 2);
    build(mid + 1, r, k * 2 + 1);
    tree[k].w = tree[k * 2].w + tree[k * 2 + 1].w;
}

void add(int k) {
    if (tree[k].l == tree[k].r) {
        tree[k].w += y;
        return;
    }
    int mid = (tree[k].l + tree[k].r) / 2;
    if (x <= mid) add(k * 2);
    else add(k * 2 + 1);
    tree[k].w = tree[k * 2].w + tree[k * 2 + 1].w;
}

void sum(int k) {
    if (tree[k].l >= x && tree[k].r <= y) {
        ans += tree[k].w;
        return;
    }
    int mid = (tree[k].l + tree[k].r) / 2;
    if (x <= mid) sum(k * 2);
    if (y > mid) sum(k * 2 + 1);
}

int main() {
    cin >> n;
    build(1, n, 1);
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> p >> x >> y;
        ans = 0;
        if (p == 1) {
            add(1);
        } else {
            sum(1);
            cout << ans << endl;
        }
    }
    return 0;
}

 

 

題目描述 Description

給你N個數，有兩種操作


1：給區間[a,b]的所有數都增加X


2：詢問第i個數是什麼？

輸入描述 Input Description

第一行一個正整數n，接下來n行n個整數，再接下來一個正整數Q，表示操作的個數. 接下來Q行每行若干個整數。如果第一個數是1，後接3個正整數a,b,X，表示在區間[a,b]內每個數增加X,如果是2，後面跟1個整數i, 表示詢問第i個位置的數是多少。

輸出描述 Output Description

對於每個詢問輸出一行一個答案

樣例輸入 Sample Input

3

1

2

3

2

1 2 3 2

2 3

樣例輸出 Sample Output

5

資料範圍及提示 Data Size & Hint

資料範圍

1<=n<=100000

1<=q<=100000

 

#include<iostream>
using namespace std;
const int maxn = 100010;
int n, m, p, x, a, b, ans;
struct node {
    int l, r, w, f;
}tree[4 * maxn + 10];

void build(int l, int r, int k) {
    tree[k].l = l;
    tree[k].r = r;
    if (l == r) {
        cin >> tree[k].w;
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, k * 2);
    build(mid + 1, r, k * 2 + 1);
    tree[k].w = tree[k * 2].w + tree[k * 2 + 1].w;
}

void down(int k) {
    tree[k * 2].f += tree[k].f;
    tree[k * 2 + 1].f += tree[k].f;
    tree[2 * k].w += tree[k].f * (tree[k * 2].r - tree[k * 2].l + 1);
    tree[2 * k + 1].w += tree[k].f * (tree[k * 2 + 1].r - tree[k * 2 + 1].l + 1);
    tree[k].f = 0;
}

void add(int k) {
    if (tree[k].l >= a && tree[k].r <= b) {
        tree[k].w += (tree[k].r - tree[k].l + 1) * x;
        tree[k].f += x;
        return;
    }
    if (tree[k].f) down(k);
    int mid = (tree[k].l + tree[k].r) / 2;
    if (a <= mid) add(k * 2);
    if (b > mid) add(k * 2 + 1);
    tree[k].w = tree[k * 2].w + tree[k * 2 + 1].w;
}



void ask(int k) {
    if (tree[k].l == tree[k].r) {
        ans = tree[k].w;
        return;
    }
    if (tree[k].f) down(k);
    int mid = (tree[k].l + tree[k].r) / 2;
    if (x <= mid) ask(k * 2);
    else ask(k * 2 + 1);
}


int main () {
    cin >> n;
    build(1, n, 1);
    cin >> m;
    for (int i = 0; i < m; i++) {
        cin >> p;
        if (p == 1) {
            cin >> a >> b >> x;
            add(1);
        } else {
            cin >> x;
            ask(1);
            cout << ans << endl;
        }
    }
    return 0;
}

 

題目描述 Description

給你N個數，有兩種操作：


1：給區間[a,b]的所有數增加X


2：詢問區間[a,b]的數的和。

輸入描述 Input Description

第一行一個正整數n，接下來n行n個整數，

 

再接下來一個正整數Q，每行表示操作的個數，

 

如果第一個數是1，後接3個正整數，

 

表示在區間[a,b]內每個數增加X,如果是2，

 

表示操作2詢問區間[a,b]的和是多少。

 

pascal選手請不要使用readln讀入

輸出描述 Output Description

對於每個詢問輸出一行一個答案

樣例輸入 Sample Input

3

1

2

3

2

1 2 3 2

2 2 3

樣例輸出 Sample Output

9

資料範圍及提示 Data Size & Hint

資料範圍

1<=n<=200000

1<=q<=200000

 

#include<iostream>
using namespace std;
const int maxn = 200010;
int n, m, p, x, a, b;
long long ans;
struct Node {
    long long l, r, w, f;
}node[4 * maxn + 10];

void build (int l, int r, int k) {
    node[k].l = l;
    node[k].r = r;
    if (l == r) {
        cin >> node[k].w;
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, k * 2);
    build(mid + 1, r, k * 2 + 1);
    node[k].w = node[k * 2].w + node[k * 2 + 1].w;
}

void down(int k) {
    node[2 * k].f += node[k].f;
    node[2 * k + 1].f += node[k].f;
    node[2 * k].w += (node[2 * k].r - node[2 * k].l + 1) * node[k].f;
    node[2 * k + 1].w += (node[2 * k + 1].r - node[2 * k + 1].l + 1) * node[k].f;
    node[k].f = 0;
}

void add(int k) {
    if (node[k].l >= a && b >= node[k].r) {
        node[k].w += (node[k].r - node[k].l + 1) * x;
        node[k].f += x;
        return;
    }
    if (node[k].f) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        add(k * 2);
    }
    if (b > mid) {
        add(k * 2 + 1);
    }
    node[k].w = node[k * 2].w + node[k * 2 + 1].w;
}

void sum(int k) {
    if (node[k].l >= a && node[k].r <= b) {
        ans += node[k].w;
        return;
    }
    if (node[k].f) down(k);
    int mid = (node[k].l + node[k].r) / 2;
    if (a <= mid) {
        sum(k * 2);
    }
    if (b > mid) {
        sum(k * 2 + 1);
    }
}

int main() {
    cin >> n;
    build(1, n, 1);
    cin >> m;
    for (int i = 0; i < m; i++) {
        cin >> p;
        ans = 0;
        if (p == 1) {
            cin >> a >> b >> x;
            add(1);
        } else {
            cin >> a >> b;
            sum(1);
            cout << ans << endl;
        }
    }
    return 0;
}

總結：其實這類的模板題寫多了就熟練了，可以進行更近一步的題目的針對訓練了，題目來源自洛古語codevs，有興趣的可以登入這倆個平臺然後將這幾個題做一做

相關推薦

線段樹模板題5題

題目描述 如題，已知一個數列，你需要進行下面兩種操作： 1.將某區間每一個數加上x 2.求出某區間每一個數的和 輸入輸出格式 輸入格式：   第一行包含兩個整數N、M，分別表示該數列數字的個數和操作的總個數。 第二行包含N個用空格分隔的整數，其中第i個數字表

[bzoj1568]李超線段樹模板題(標誌永久化)

space str ios idt .cn () oid algorithm height 題意：要求在平面直角坐標系下維護兩個操作： 1.在平面上加入一條線段。記第i條被插入的線段的標號為i。 2.給定一個數k,詢問與直線 x = k相交的線段中，交點最靠上的線段的編

維護序列 洛谷線段樹模板題2

hint reg ref org arch ucc search efi str 1104: 維護序列seq Time Limit3000 msMemory Limit512072 KBytesJudgeStandard JudgeSolved71Submit234 Sub

[線段樹模板題] 線段樹2

洛谷原題 第二次做 線段樹2 了，之前研究了兩節晚自習自以為完全理解了，但是今天寫還是有一點小差錯，值得反思。 稍微總結下線段樹2的要點。 <1> 乘法標記影響加法標記，更新 乘法標記 時應將對應的 加法標記 乘上 乘法標記乘的值(key) <2> 標記下傳中 乘法標

線段樹 模板題

線段樹 Problem Description 已知一個數列，你需要進行下面兩種操作： 1.將某區間每一個數加上x 2.求出某區間每一個數的和 Input 第一行包含兩個整數N、M，分別表示該數列數字的個數和操作的總個數。 第二行包含N個用空格分隔的整數，其中第i個數字表示數列第

bzoj1012（線段樹模板題）

題目讀了三遍才讀懂，對於蒟蒻來說，看上去很難得樣子，實際就是線段樹的單點更新，然後求區間最值，無奈之前還想著怎麼建樹插進去。。結果RE n次，感覺自己水的一匹，唉~ 做題效率極低。。。。 真是被自己蠢哭了 #include<iostream> #i

HDU 1166 敵兵佈陣（線段樹模板題）

敵兵佈陣 Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 127082    Accepted Submissi

線段樹模板題（結構體&一維陣列）（區間最值，求和）

1099: [視訊]線段樹（元問題byscy）線性結構求極值和修改 時間限制: 1 Sec 記憶體限制: 128 MB 提交: 496 解決: 165 [提交][狀態][討論版] 題目描述 【題意】 給出N個數，兩種操作： 1、C x y：修改

線段樹題解（3題）

integer pre contain 恰恰 sam 編號 更改 splay article A - 敵兵布陣 C國的死對頭A國這段時間正在進行軍事演習，所以C國間諜頭子Derek和他手下Tidy又開始忙乎了。A國在海岸線沿直線布置了N個工兵營地,Derek和Tidy的

HDU 1698 Just a Hook （線段樹區間更新入門題）

follow and iostream http span meta ali pos num Just a Hook Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/O

【hdu 5692 Snacks】【dfs序】【線段樹】【好題】

【連結】 http://acm.hdu.edu.cn/showproblem.php?pid=5692 【題意】 樹上兩種操作： 0 x y 將x的權重變為y 1 x 求出從0出發，經過x的路徑的最距離和 【分析】 其實就是求一棵子樹x裡到0點路徑權值和最大的點的那個權值

code forces 383C（線段樹）經典好題

題意： 兩種操作，1.給出一個節點u，u的權值加上val，u的下一層孩子權值加上-val,下下層孩子加上val,一直 2.查詢節點u的權值 思路：將樹進行離散化，跑個dfs，然後節點和它的孩子節點都在一個連續的區間內。         更新的時候，因為對於每一層的更新情況不

主席樹模板總結及題集

介紹篇：http://blog.csdn.net/metalseed/article/details/8045038  -> 理解篇（配圖比較生動）：http://blog.csdn.net/regina8023/article/details/41910615  -

HDU 5692 Snacks (DFS序 + 線段樹區間更新 好題)

  題目連結：http://acm.hdu.edu.cn/showproblem.php?pid=5692 題目分析：其實就是求一棵子樹x裡到0點路徑權值和最大的點的那個權值和，因為是對一棵子樹的所有值，所以容易想到用DFS序來處理，改變x點權值則其子樹所有點到0點的路徑權值和都要更新，這樣就變成區間更新求最

[線段樹]HDU-1754板子題入門ver

uil 開始 圖片 board alt 分享圖片 繼續 || 新的 HDU-1754 線段樹數組請開到四倍 眾所周知數組開小會導致re tle wa等一系列問題orz 　　板子就是板子，數組從零開始或是從一開始都沒什麽問題，就是2*root+1還是2*root+

線段樹模板

print dac gif date aps 所在 ret 線段樹模板 核心 1、求區間和 1 #include <cstdio> 2 #include <iostream> 3 using namespace std; 4 const

線段樹模板——區間乘 && 區間加 && 區間求和

markdown 區間求和 www. -m 閱讀 https d+ pre 題目 線段樹模板——區間乘 && 區間加 && 區間求和 <題目鏈接> 來自一個NOIP沒學好的省選選手——本應早在NOIP之前學好的內容。 #i

P3373 線段樹模板

gif gpo pri ret ace d+ urn col play 好，這是一個線段樹模板。 1 #include <cstdio> 2 using namespace std; 3 const long long int N=1000010

線段樹模板1 [Luogu P3372]

str 填充 namespace 清空 flag pan 斷開 nod 點數據 代碼+註釋： 1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 5 in

線段樹模板(單點更新）

div ret onclick 更新 turn space view date span 1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #inc