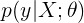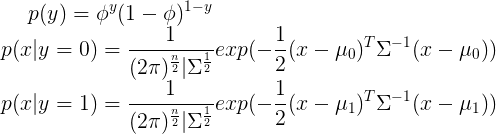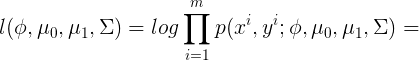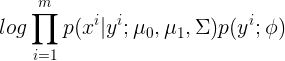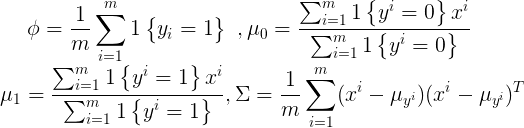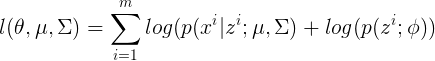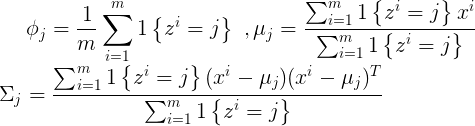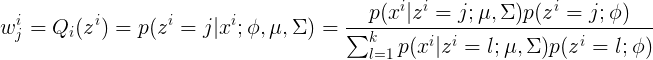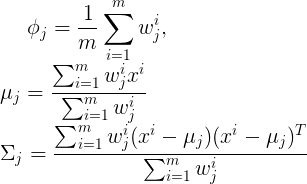1.15 Generative Learning Algorithm:GDA and Mixture of Gaussians/GMM
1. 生成學習演算法(Generative Learning Algorithm)與判別學習演算法(Discriminative Learning Algorithm):
之前涉及到的迴歸類模型就是DLA的一類,是直接對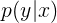
建模,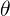
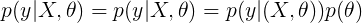
而GLA則是對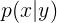
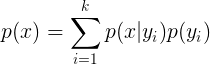
利用貝葉斯公式: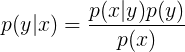
現在我學到的生成學習分類演算法有兩類:GDA(高斯判別分析)和Naive Bayes(樸素貝葉斯)。
當類別標記不知道時,即未觀測,分類問題就是一個聚類問題。將未被觀測到的類標記當成隱隨機變數(latent random variable),通過EM演算法,就可以求解聚類問題。這篇部落格記錄了分類問題下GDA以及用於分類高斯混合模型。
2.GDA:二分類:
(1)
模型假設: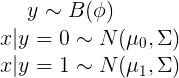
因為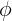
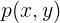
估計,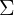
估計出來的結果是:
(2)與Logistic Regression的對比:
logistic regression有著更弱的假設,而高斯判別分析需要假設更強一些。
(3)多分類高斯判別分析:
令z表示類標記,有:
最終結果如下:
PS:這裡有一個問題就是:為什麼二分類時 用的是一個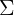
3.Mixture of Gaussians:
對於混合高斯用於聚類,需要知道EM演算法的相關知識,見1.16
優化問題同1中(3)所記錄的:
但是因為z是一個隱變數,所以直接計算比較困難,所以使用EM迭代計算。演算法推導還沒完全搞懂,這裡不記錄。
演算法流程如下:
Repeat until convergence{
E-step: For each i,j,set
M-step: Set
}