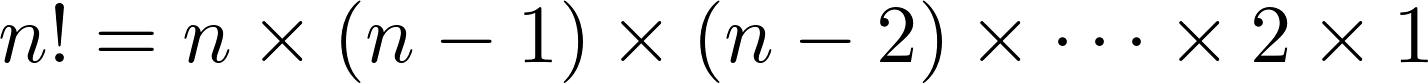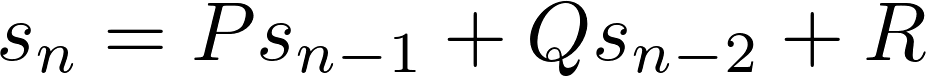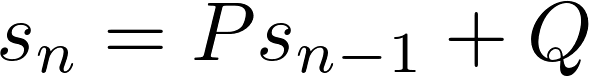Itertools in Python 3, By Example
It has been called a “gem” and “pretty much the coolest thing ever,” and if you have not heard of it, then you are missing out on one of the greatest corners of the Python 3 standard library: itertools.
A handful of excellent resources exist for learning what functions are available in the itertools
The thing about itertools, though, is that it is not enough to just know the definitions of the functions it contains. The real power lies in composing these functions to create fast, memory-efficient, and good-looking code.
This article takes a different approach. Rather than introducing itertools
A word of warning: this article is long and intended for the intermediate-to-advanced Python programmer. Before diving in, you should be confident using iterators and generators in Python 3, multiple assignment, and tuple unpacking. If you aren’t, or if you need to brush up on your knowledge, consider checking out the following before reading on:
Free Bonus: Click here to get our itertools cheat sheet that summarizes the techniques demonstrated in this tutorial.
All set? Let’s start the way any good journey should—with a question.
What Is Itertools and Why Should You Use It?
According to the itertools docs, it is a “module [that] implements a number of iterator building blocks inspired by constructs from APL, Haskell, and SML… Together, they form an ‘iterator algebra’ making it possible to construct specialized tools succinctly and efficiently in pure Python.”
Loosely speaking, this means that the functions in itertools “operate” on iterators to produce more complex iterators. Consider, for example, the built-in zip() function, which takes any number of iterables as arguments and returns an iterator over tuples of their corresponding elements:
>>> list(zip([1, 2, 3], ['a', 'b', 'c'])) [(1, 'a'), (2, 'b'), (3, 'c')]
How, exactly, does zip() work?
[1, 2, 3] and ['a', 'b', 'c'], like all lists, are iterable, which means they can return their elements one at a time. Technically, any Python object that implements the .__iter__() or .__getitem__() methods is iterable. (See the Python 3 docs glossary for a more detailed explanation.)
>>> iter([1, 2, 3, 4]) <list_iterator object at 0x7fa80af0d898>
Under the hood, the zip() function works, in essence, by calling iter() on each of its arguments, then advancing each iterator returned by iter() with next() and aggregating the results into tuples. The iterator returned by zip() iterates over these tuples.
The map() built-in function is another “iterator operator” that, in its simplest form, applies a single-parameter function to each element of an iterable one element at a time:
>>> list(map(len, ['abc', 'de', 'fghi'])) [3, 2, 4]
The map() function works by calling iter() on its second argument, advancing this iterator with next() until the iterator is exhausted, and applying the function passed to its first argument to the value returned by next() at each step. In the above example, len() is called on each element of ['abc', 'de', 'fghi'] to return an iterator over the lengths of each string in the list.
Since iterators are iterable, you can compose zip() and map() to produce an iterator over combinations of elements in more than one iterable. For example, the following sums corresponding elements of two lists:
>>> list(map(sum, zip([1, 2, 3], [4, 5, 6]))) [5, 7, 9]
This is what is meant by the functions in itertools forming an “iterator algebra.” itertools is best viewed as a collection of building blocks that can be combined to form specialized “data pipelines” like the one in the example above.
Historical Note: In Python 2, the built-in
zip()andmap()functions do not return an iterator, but rather a list. To return an iterator, theizip()andimap()functions ofitertoolsmust be used. In Python 3,izip()andimap()have been removed fromitertoolsand replaced thezip()andmap()built-ins. So, in a way, if you have ever usedzip()ormap()in Python 3, you have already been usingitertools!
There are two main reasons why such an “iterator algebra” is useful: improved memory efficiency (via lazy evaluation) and faster execuction time. To see this, consider the following problem:
Given a list of values
inputsand a positive integern, write a function that splitsinputsinto groups of lengthn. For simplicity, assume that the length of the input list is divisible byn. For example, ifinputs = [1, 2, 3, 4, 5, 6]andn = 2, your function should return[(1, 2), (3, 4), (5, 6)].
Taking a naive approach, you might write something like this:
def naive_grouper(inputs, n): num_groups = len(inputs) // n return [tuple(inputs[i*n:(i+1)*n]) for i in range(num_groups)]
When you test it, you see that it works as expected:
>>>>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] >>> naive_grouper(nums, 2) [(1, 2), (3, 4), (5, 6), (7, 8), (9, 10)]
What happens when you try to pass it a list with, say, 100 million elements? You will need a whole lot of available memory! Even if you have enough memory available, your program will hang for a while until the output list is populated.
To see this, store the following in a script called naive.py:
def naive_grouper(inputs, n): num_groups = len(inputs) // n return [tuple(inputs[i*n:(i+1)*n]) for i in range(num_groups)] for _ in naive_grouper(range(100000000), 10): pass
From the console, you can use the time command (on UNIX systems) to measure memory usage and CPU user time. Make sure you have at least 5GB of free memory before executing the following:
$ time -f "Memory used (kB): %M\nUser time (seconds): %U" python3 naive.py Memory used (kB): 4551872 User time (seconds): 11.04
Note: On Ubuntu, you may need to run
/usr/bin/timeinstead oftimefor the above example to work.
The list and tuple implementation in naive_grouper() requires approximately 4.5GB of memory to process range(100000000). Working with iterators drastically improves this situation. Consider the following:
def better_grouper(inputs, n): iters = [iter(inputs)] * n return zip(*iters)
There’s a lot going on in this little function, so let’s break it down with a concrete example. The expression [iters(inputs)] * n creates a list of n references to the same iterator:
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] >>> iters = [iter(nums)] * 2 >>> list(id(itr) for itr in iters) # IDs are the same. [139949748267160, 139949748267160]
Next, zip(*iters) returns an iterator over pairs of corresponding elements of each iterator in iters. When the first element, 1, is taken from the “first” iterator, the “second” iterator now starts at 2 since it is just a reference to the “first” iterator and has therefore been advanced one step. So, the first tuple produced by zip() is (1, 2).
At this point, “both” iterators in iters start at 3, so when zip() pulls 3 from the “first” iterator, it gets 4 from the “second” to produce the tuple (3, 4). This process continues until zip() finally produces (9, 10) and “both” iterators in iters are exhausted:
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] >>> list(better_grouper(nums, 2)) [(1, 2), (3, 4), (5, 6), (7, 8), (9, 10)]
The better_grouper() function is better for a couple of reasons. First, without the reference to the len() built-in, better_grouper() can take any iterable as an argument (even infinite iterators). Second, by returning an iterator rather than a list, better_grouper() can process enormous iterables without trouble and uses much less memory.
Store the following in a file called better.py and run it with time from the console again:
def better_grouper(inputs, n): iters = [iter(inputs)] * n return zip(*iters) for _ in better_grouper(range(100000000), 10): pass
$ time -f "Memory used (kB): %M\nUser time (seconds): %U" python3 better.py Memory used (kB): 7224 User time (seconds): 2.48
That’s a whopping 630 times less memory used than naive.py in less than a quarter of the time!
Now that you’ve seen what itertools is (“iterator algebra”) and why you should use it (improved memory efficiency and faster execution time), let’s take a look at how to take better_grouper() to the next level with itertools.
The grouper Recipe
The problem with better_grouper() is that it doesn’t handle situations where the value passed to the second argument isn’t a factor of the length of the iterable in the first argument:
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] >>> list(better_grouper(nums, 4)) [(1, 2, 3, 4), (5, 6, 7, 8)]
The elements 9 and 10 are missing from the grouped output. This happens because zip() stops aggregating elements once the shortest iterable passed to it is exhausted. It would make more sense to return a third group containing 9 and 10.
To do this, you can use itertools.zip_longest(). This function accepts any number of iterables as arguments and a fillvalue keyword argument that defaults to None. The easiest way to get a sense of the difference between zip() and zip_longest() is to look at some example output:
>>> import itertools as it >>> x = [1, 2, 3, 4, 5] >>> y = ['a', 'b', 'c'] >>> list(zip(x, y)) [(1, 'a'), (2, 'b'), (3, 'c')] >>> list(it.zip_longest(x, y)) [(1, 'a'), (2, 'b'), (3, 'c'), (4, None), (5, None)]
With this in mind, replace zip() in better_grouper() with zip_longest():
import itertools as it def grouper(inputs, n, fillvalue=None): iters = [iter(inputs)] * n return it.zip_longest(*iters, fillvalue=fillvalue)
Now you get a better result:
>>>>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] >>> print(list(grouper(nums, 4))) [(1, 2, 3, 4), (5, 6, 7, 8), (9, 10, None, None)]
The grouper() function can be found in the Recipes section of the itertools docs. The recipes are an excellent source of inspiration for ways to use itertools to your advantage.
Note: From this point forward, the line import itertools as it will not be included at the beginning of examples. All itertools methods in code examples are prefaced with it. The module import is implied.
If you get a NameError: name 'itertools' is not defined or a NameError: name 'it' is not defined exception when running one of the examples in this tutorial you’ll need to import the itertools module first.
Et tu, Brute Force?
Here’s a common interview-style problem:
You have three $20 dollar bills, five $10 dollar bills, two $5 dollar bills, and five $1 dollar bills. How many ways can you make change for a $100 dollar bill?
To “brute force” this problem, you just start listing off the ways there are to choose one bill from your wallet, check whether any of these makes change for $100, then list the ways to pick two bills from your wallet, check again, and so on and so forth.
But you are a programmer, so naturally you want to automate this process.
First, create a list of the bills you have in your wallet:
bills = [20, 20, 20, 10, 10, 10, 10, 10, 5, 5, 1, 1, 1, 1, 1]
A choice of k things from a set of n things is called a combination, and itertools has your back here. The itertools.combinations() function takes two arguments—an iterable inputs and a positive integer n—and produces an iterator over tuples of all combinations of n elements in inputs.
For example, to list the combinations of three bills in your wallet, just do:
>>>>>> list(it.combinations(bills, 3)) [(20, 20, 20), (20, 20, 10), (20, 20, 10), ... ]
To solve the problem, you can loop over the positive integers from 1 to len(bills), then check which combinations of each size add up to $100:
>>> makes_100 = [] >>> for n in range(1, len(bills) + 1): ... for combination in it.combinations(bills, n): ... if sum(combination) == 100: ... makes_100.append(combination)
If you print out makes_100, you will notice there are a lot of repeated combinations. This makes sense because you can make change for $100 with three $20 dollar bills and four $10 bills, but combinations() does this with the first four $10 dollars bills in your wallet; the first, third, fourth and fifth $10 dollar bills; the first, second, fourth and fifth $10 bills; and so on.
To remove duplicates from makes_100, you can convert it to a set:
>>> set(makes_100) {(20, 20, 10, 10, 10, 10, 10, 5, 1, 1, 1, 1, 1), (20, 20, 10, 10, 10, 10, 10, 5, 5), (20, 20, 20, 10, 10, 10, 5, 1, 1, 1, 1, 1), (20, 20, 20, 10, 10, 10, 5, 5), (20, 20, 20, 10, 10, 10, 10)}
So, there are five ways to make change for a $100 bill with the bills you have in your wallet.
Here’s a variation on the same problem:
How many ways are there to make change for a $100 bill using any number of $50, $20, $10, $5, and $1 dollar bills?
In this case, you don’t have a pre-set collection of bills, so you need a way to generate all possible combinations using any number of bills. For this, you’ll need the itertools.combinations_with_replacement() function.
It works just like combinations(), accepting an iterable inputs and a positive integer n, and returns an iterator over n-tuples of elements from inputs. The difference is that combinations_with_replacement() allows elements to be repeated in the tuples it returns.
For example:
>>>>>> list(it.combinations_with_replacement([1, 2], 2)) [(1, 1), (1, 2), (2, 2)]
Compare that to combinations():
>>> list(it.combinations([1, 2], 2)) [(1, 2)]
Here’s what the solution to the revised problem looks like:
>>>>>> bills = [50, 20, 10, 5, 1] >>> make_100 = [] >>> for n in range(1, 101): ... for combination in it.combinations_with_replacement(bills, n): ... if sum(combination) == 100: ... makes_100.append(combination)
In this case, you do not need to remove any duplicates since combinations_with_replacement() won’t produce any:
>>> len(makes_100) 343
If you run the above solution, you may notice that it takes a while for the output to display. That is because it has to process 96,560,645 combinations!
Another “brute force” itertools function is permutations(), which accepts a single iterable and produces all possible permutations (rearrangements) of its elements:
>>> list(it.permutations(['a', 'b', 'c'])) [('a', 'b', 'c'), ('a', 'c', 'b'), ('b', 'a', 'c'), ('b', 'c', 'a'), ('c', 'a', 'b'), ('c', 'b', 'a')]
Any iterable of three elements will have six permutations, and the number of permutations of longer iterables grows extremely fast. In fact, an iterable of length n has n! permutations, where
To put this in perspective, here’s a table of these numbers for n = 1 to n = 10:
| n | n! |
|---|---|
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5,040 |
| 8 | 40,320 |
| 9 | 362,880 |
| 10 | 3,628,800 |
The phenomenon of just a few inputs producing a large number of outcomes is called a combinatorial explosion and is something to keep in mind when working with combinations(), combinations_with_replacement(), and permutations().
It is usually best to avoid brute force algorithms, although there are times you may need to use one (for example, if the correctness of the algorithm is critical, or every possible outcome must be considered). In that case, itertools has you covered.
Section Recap
In this section you met three itertools functions: combinations(), combinations_with_replacement(), and permutations().
Let’s review these functions before moving on:
itertools.combinations Example
>>>
combinations(iterable, n)Return successive n-length combinations of elements in the iterable.
>>> combinations([1, 2, 3], 2) (1, 2), (1, 3), (2, 3)
itertools.combinations_with_replacement Example
>>>
combinations_with_replacement(iterable, n)Return successive n-length combinations of elements in the iterable allowing individual elements to have successive repeats.
>>> combinations_with_replacement([1, 2], 2) (1, 1), (1, 2), (2, 2)
itertools.permutations Example
>>>
permutations(iterable, n=None)Return successive n-length permutations of elements in the iterable.
>>> permutations('abc') ('a', 'b', 'c'), ('a', 'c', 'b'), ('b', 'a', 'c'), ('b', 'c', 'a'), ('c', 'a', 'b'), ('c', 'b', 'a')
Sequences of Numbers
With itertools, you can easily generate iterators over infinite sequences. In this section, you will explore numeric sequences, but the tools and techniques seen here are by no means limited to numbers.
Evens and Odds
For the first example, you will create a pair of iterators over even and odd integers without explicitly doing any arithmetic. Before diving in, let’s look at an arithmetic solution using generators:
>>>>>> def evens(): ... """Generate even integers, starting with 0.""" ... n = 0 ... while True: ... yield n ... n += 2 ... >>> evens = evens() >>> list(next(evens) for _ in range(5)) [0, 2, 4, 6, 8] >>> def odds(): ... """Generate odd integers, starting with 1.""" ... n = 1 ... while True: ... yield n ... n += 2 ... >>> odds = odds() >>> list(next(odds) for _ in range(5)) [1, 3, 5, 7, 9]
That is pretty straightforward, but with itertools you can do this much more compactly. The function you need is itertools.count(), which does exactly what it sounds like: it counts, starting by default with the number 0.
>>> counter = it.count() >>> list(next(counter) for _ in range(5)) [0, 1, 2, 3, 4]
You can start counting from any number you like by setting the start keyword argument, which defaults to 0. You can even set a step keyword argument to determine the interval between numbers returned from count()—this defaults to 1.
With count(), iterators over even and odd integers become literal one-liners:
>>> evens = it.count(step=2) >>> list(next(evens) for _ in range(5)) [0, 2, 4, 6, 8] >>> odds = it.count(start=1, step=2) >>> list(next(odds) for _ in range(5)) [1, 3, 5, 7, 9]
Ever since Python 3.1, the count() function also accepts non-integer arguments:
>>> count_with_floats = it.count(start=0.5, step=0.75) >>> list(next(count_with_floats) for _ in range(5)) [0.5, 1.25, 2.0, 2.75, 3.5]
You can even pass it negative numbers:
>>>>>> negative_count = it.count(start=-1, step=-0.5) >>> list(next(negative_count) for _ in range(5)) [-1, -1.5, -2.0, -2.5, -3.0]
In some ways, count() is similar to the built-in range() function, but count() always returns an infinite sequence. You might wonder what good an infinite sequence is since it’s impossible to iterate over completely. That is a valid question, and I admit the first time I was introduced to infinite iterators, I too didn’t quite see the point.
The example that made me realize the power of the infinite iterator was the following, which emulates the behavior of the built-in enumerate() function:
>>> list(zip(it.count(), ['a', 'b', 'c'])) [(0, 'a'), (1, 'b'), (2, 'c')]
It is a simple example, but think about it: you just enumerated a list without a for loop and without knowing the length of the list ahead of time.
Recurrence Relations
A recurrence relation is a way of describing a sequence of numbers with a recursive formula. One of the best-known recurrence relations is the one that describes the Fibonacci sequence.
The Fibonacci sequence is the sequence 0, 1, 1, 2, 3, 5, 8, 13, .... It starts with 0 and 1, and each subsequent number in the sequence is the sum of the previous two. The numbers in this sequence are called the Fibonacci numbers. In mathematical notation, the recurrence relation describing the n-th Fibonacci number looks like this:
Note: If you search Google, you will find a host of implementations of these numbers in Python. You can find a recursive function that produces them in the Thinking Recursively in Python article here on Real Python.
It is common to see the Fibonacci sequence produced with a generator:
def fibs(): a, b = 0, 1 while True: yield a a, b = b, a + b
The recurrence relation describing the Fibonacci numbers is called a second order recurrence relation because, to calculate the next number in the sequence, you need to look back two numbers behind it.
In general, second order recurrence relations have the form:
Here, P, Q, and R are constants. To generate the sequence, you need two initial values. For the Fibonacci numbers, P = Q = 1, R = 0, and the initial values are 0 and 1.
As you might guess, a first order recurrence relation has the following form:
There are countless sequences of numbers that can be described by first and second order recurrence relations. For example, the positive integers can be described as a first order recurrence relation with P = Q = 1 and initial value 1. For the even integers, take P = 1 and Q = 2 with initial value 0.
In this section, you will construct functions for producing any sequence whose values can be described with a first or second order recurrence relation.
First Order Recurrence Relations
You’ve already seen how count() can generate the sequence of non-negative integers, the even integers, and the odd integers. You can also use it to generate the sequence 3n = 0, 3, 6, 9, 12, … and 4n = 0, 4, 8, 12, 16, ….
count_by_three = it.count(step=3) count_by_four = it.count(step=4)
In fact, count() can produce sequences of multiples of any number you wish. These sequences can be described with first-order recurrence relations. For example, to generate the sequence of multiples of some number n, just take P = 1, Q = n, and initial value 0.
Another easy example of a first-order recurrence relation is the constant sequence n, n, n, n, n…, where n is any value you’d like. For this sequence, set P = 1 and Q = 0 with initial value n. itertools provides an easy way to implement this sequence as well, with the repeat() function:
all_ones = it.repeat(1) # 1, 1, 1, 1, ... all_twos = it.repeat(2) # 2, 2, 2, 2, ...
If you need a finite sequence of repeated values, you can set a stopping point by passing a positive integer as a second argument:
five_ones = it.repeat(1, 5) # 1, 1, 1, 1, 1 three_fours = it.repeat(4, 3) # 4, 4, 4
What may not be quite as obvious is that the sequence 1, -1, 1, -1, 1, -1, ... of alternating 1s and -1s can also be described by a first order recurrence relation. Just take P = -1, Q = 0, and initial value 1.
There’s an easy way to generate this sequence with the itertools.cycle() function. This function takes an iterable inputs as an argument and returns an infinite iterator over the values in inputs that returns to the beginning once the end of inputs is reached. So, to produce the alternating sequence of 1s and -1s, you could do this:
alternating_ones = it.cycle([1, -1]) # 1, -1, 1, -1, 1, -1, ...
The goal of this section, though, is to produce a single function that can generate any first order recurrence relation—just pass it P, Q, and an initial value. One way to do this is with itertools.accumulate().
The accumulate() function takes two arguments—an iterable inputs and a binary function func (that is, a function with exactly two inputs)—and returns an iterator over accumulated results of applying func to elements of inputs. It is roughly equivalent to the following generator:
def accumulate(inputs, func): itr = iter(inputs) prev = next(itr) for cur in itr: yield prev prev = func(prev, cur)
For example:
>>>>>> import operator >>> list(it.accumulate([1, 2, 3, 4, 5], operator.add)) [1, 3, 6, 10, 15]
The first value in the iterator returned by accumulate() is always the first value in the input sequence. In the above example, this is 1—the first value in [1, 2, 3, 4, 5].
The next value in the output iterator is the sum of the first two elements of the input sequence: add(1, 2) = 3. To produce the next value, accumulate() takes the result of add(1, 2) and adds this to the third value in the input sequence:
add(3, 3) = add(add(1, 2), 3) = 6
The fourth value produced by accumulate() is add(add(add(1, 2), 3), 4) = 10, and so on.
The second argument of accumulate() defaults to operator.add(), so the previous example can be simplified to:
>>> list(it.accumulate([1, 2, 3, 4, 5])) [1, 3, 6, 10, 15]
Passing the built-in min() to accumulate() will keep track of a running minimum: