原文參考
斯坦福機器學習cs229-2-Generative Learning algorithms
https://mathdept.iut.ac.ir/sites/mathdept.iut.ac.ir/files/AGRESTI.PDF
http://data.princeton.edu/wws509/notes/c4a.pdf
http://www.cnblogs.com/ooon/p/5845917.html

回顧上節文章中提到的logistic和probit模型：

我們假定了潛變數模型
y*=xβ+u
(y=1，when y*>0; y=0，when y*<=0)
中的殘差變數服從對應的是logistic分佈或正態分佈，並且我們假定
$P(y=1|x)=G(β_0+β_1x_1+β_2x_2+…+β_nx_n)=G(β_0+xβ)=G(xβ) $
的變換函式G()為對應的"標準的Logistic隨機變數的累計分佈函式"或
“標準的正態隨機變數的累計分佈函式”。

那麼這兩個模型的因變數都是離散的或者說是定性( or 分類)變數。
這類變數除了第一節討論的名義變數中的二元變數外，還有下面三種形式：

• 名義變數中的多元變數
• 定序變數
• 計數變數

備註：
1，由0-1二元變數的期望等於P(Y=1|x)的概率可知，我們的研究問題也可以是針對因變數為概率型
2，對於因變數為資料值的資料，也是可以分組為上述幾種離散資料的形式的
3，對於因變數的意義為“佔比”時，可以轉換為計數問題
4，根據變數的層級關係：名義變數<定序變數 <計數或者說間隔變數，我們的模型適用情況如下，低層的模型可以適用於高層，反之不成立。舉例說明，針對名義變數設計出來模型可以適用於定序變數，但是針對定序變數設計出來的模型不適用於名義變數。但是要記住一點，這種跨層級模型使用方式並不是最優的，因為模型並沒有充分利用資料中的資訊。

一，離散變數的概率分佈
1，伯努利分佈(0-1分佈)

略...
例子：扔硬幣正面朝上的概率

2，二項分佈

略...
np之積>5時，分佈近似正態分佈
例子：扔硬幣k次正面朝上的概率p

3，多項分佈

略...
例子：扔骰子，k次中均由其中一個面(比如說點數6)朝上的概率

4，負二項分佈

略...
例子：扔硬幣，剛好在第r+k次試驗出現第r次正面朝上的概率

5，泊松分佈

X:一定時間或空間內，稀有事件發生的個數，一般服從泊松分佈
當二項分佈的p很小，n很大時，極限分佈為泊松分佈
當然，二項分佈、泊松分佈與正態分佈之間都有關係，[參見](https://wenku.baidu.com/view/6cd5121da300a6c30c229fbb.html)
 

5.1 泊松分佈的：overdispersion
我們知道，理論上，泊松分佈的期望和方差是相等的，但此時若觀測到的樣本方差系統地大於分佈假設下的方差，就出現了所謂的 “超散佈性”(overdispersion)，類似地，若出現方差偏小的情況，也就相應出現了 “超聚集性”(underdispersion)。

5.2 當泊松分佈出現overdispersion現象時，通常可以轉換成使用負二項分佈進行建模。
負二項分佈可以看成是廣義的泊松分佈，它可由 X|λ∼Poisson(λ) 且 λ∼Gamma(α,β)，推導得到。

(1) 如果， $X|λ∼Poisson(λ) ，則 f(x|λ)=Pr(X=x|λ)=\frac{λ^xe^{−λ}}{x!}$
(2) 且， $λ∼Gamma(α,β)，則 f(λ)= \frac{a^{β}{Г(β)}λ}{β-1}e^{-aλ} $
(3) 我們可以得到，聯合概率
$Pr(X=x|λ)Pr(λ)$
$=\frac{λ^xe{−λ}}{x!}*\frac{a^{β}{Г(β)}λ}{β-1}e^{-aλ} $
$=\frac{a^{β}{x!•Г(β)}λ}{x+β-1}e^{-(a+1)λ} $

則，x的邊際分佈即為負二項分佈：
$Pr(X=x)=\frac{a^β}{x!•Г(β)}\int^{∞}_{0}λ^{x+β-1}e^{-(a+1)λ}dλ$
$=C_{n+β-1}^{n}(\frac{a}{a+1})^β(\frac{1}{a+1})^n$

表示，第r=β次成功的負二項分佈，且成功的概率為 $p=\frac{a}{a+1}$，

6，引入先驗資訊

二項分佈或多項分佈中，隨機事件發生的概率是固定的，但是如果對於總體中的不同個體，，隨機事件發生是概率是不同時，在貝葉斯研究體系下，我們就可以引入先驗概率對不同個體的發生概率進行的估計，然後再根據後驗概率進行調整。

6.1 共軛分佈

如果先驗分佈 p(θ) 和似然函式 p(X|θ) 可以使得先驗 p(θ) 和後驗分佈 p(θ|X) 有相同的形式，那麼就稱先驗分佈與似然函式是共軛分佈.

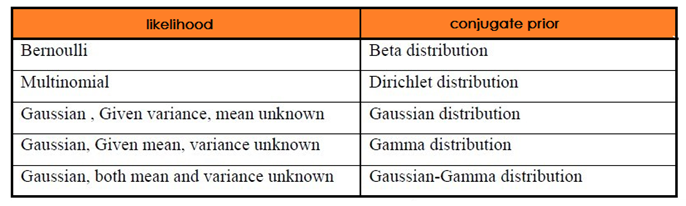
共軛性質：

• 當先驗為 Beta ，似然為 Binomial分佈時，後驗仍然為 Beta ，但是這裡的 Beta 是融入了 Binomial分佈的計數的;
• 當先驗為 Dirichlet，似然為 Multinomial 分佈時，後驗仍然為 Dirichlet，但是這裡的 Dirichlet是融入了 Multinomial 分佈的計數的.

6.2 Beta-Binomial distribution
假設，X|π∼Bin(n,π)，π∼Beta(α,β)
我們就可以根據資料得到π的先驗概率，進而計算π的後驗概率，最終推斷出似然函式。

6.3 Dirichlet-MultiNomial distribution
略

二，Poisson 迴歸

當因變數研究的是計數或比率問題時，我們假設殘差u服從Poisson分佈（迴歸分析中假定x是確定性變數，由於殘差服從泊松分佈，所以因變數y也服從於泊松分佈），G()變換為指數函式exp() (連線函式link=log())。則，此時對應的迴歸方程，則是Poisson迴歸。

1）Poisson分佈
假設隨機變數Y，服從引數為μ的泊松分佈，則y=0,1,2…整數值的概率分佈如下：
$Pr\{Y=y\}=\frac{e^{-μ}μ^y}{y!}$

性質1：
且，滿足(μ>0):
$E(Y)=var(Y)=μ$

從上式可知，任何影響均值的因素都會影響到方差，所以，同方差性假設不再適用與泊松資料。

性質2：
如果， $Y_{1}$ ~ $P(μ_1)$， $Y_{2}$ ~ $P(μ_2)$，則 $Y_{1}+Y_{2}$ ~ $P(μ_1+μ_2)$

2）Poisson迴歸

假設我們有n個觀測值， $y_1,y_2...,y_n$是分別服從泊松分佈的隨機變數，且 $Y_{i}$ ~ $P(μ_i)$

（a）假設隨機變數的均值(同時為方差)為 $μ_i$與解釋變數x成簡單線性關係：

$μ_i$~ $x_i&#x27;β$

上式缺點：公式左側非負，而右側是實數

（b）log-linear變換

$log(μ_i)$~ $x_i&#x27;β$ 則， $μ_i$~ $exp\{x_i&#x27;β\}$

與第七章將要講到的加法模型不同，該模型表示的是乘法效應

3）比率問題
單位時間或空間上的計數即為比率，對於泊松分佈來說，問題轉化為u/t
$log(μ/t)=α+βx$
$log(μ)−log(t)=α+βx$
$log(μ)=α+βx+log(t)$
$\mu =e$