1.AvlTree的定義

           AVL (Adelson Velskii和 Landis)樹是帶有平衡條件的二叉查詢樹。這個平衡條件必須容易保持，而且它必須保證樹的深度是O（log N）。最簡單的想法是要求左右子樹具有相同的高度。

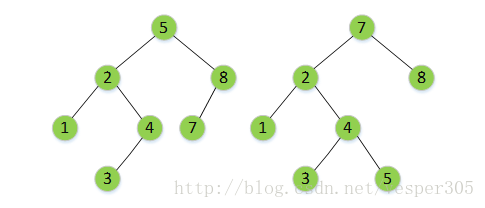
    一般限制為：一棵AVL樹是其每個節點的左子樹和右子樹的高度最多差1的二叉查詢樹。（空樹的高度定義為-1，樹中葉子的高度為0，往根上遞增）

    如上圖中，左邊就是一棵AVL樹，而右邊則不是一棵AVL樹，因為節點7的左子樹高度為2，右子樹的高度為0。

2.插入操作的問題

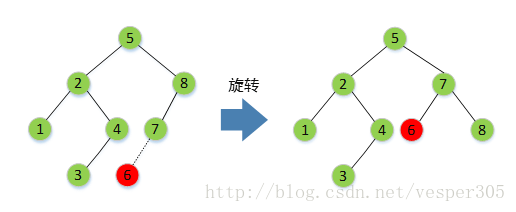
    在對AVL樹進行插入操作的時候，隱含的困難在於，插入一個節點可能破壞

    所以一般發生這種情況，我們需要把AVL樹的平衡性質恢復之後才能算是插入這一步驟完成。事實上，我們只需要根據樹的實際結構進行幾種簡單的旋轉（rotation）操作就可以讓樹恢復AVL樹的平衡性質。

2.1.四種情況，兩種分類處理

根據樹型結構的不同，我們將分成四種情況來進行旋轉處理。

讓我們把必須重新平衡的節點叫做a。由於任意節點最多有兩個兒子，因此高度不平衡時，a點的兩棵子樹的高度差2。容易看出這種不平衡可能出現在下面四種情況中。

1.對a的左兒子的左子樹進行一次插入。

2.對a的左兒子的右子樹進行一次插入。

3.對a的右兒子的左子樹進行一次插入。

4.對a的右兒子的右子樹進行一次插入。

進行旋轉處理的時候分成兩種大類處理：單旋轉和雙旋轉。

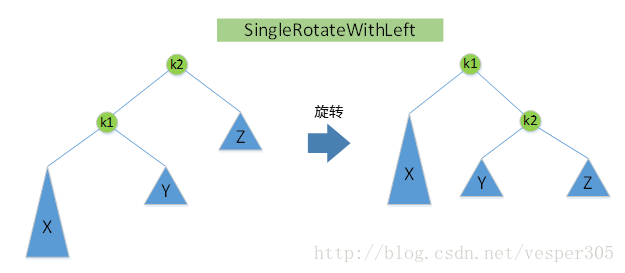
我們知道之所以會出現不平衡是由於進行插入操作之後某些節點的深度過深導致不平衡。上圖中是由於上一步在子樹Z的底部進行插入操作之後導致k1節點的左右子樹失衡。按照AVL樹的定義，此時k1右子樹的深度比k1左子樹的深度大2。按照上圖的方式進行旋轉之後k2的左子樹深度加1，而右子樹深度不變，因此重新回到平衡。

觀察上圖我們可以發現，在整個旋轉的過程中變化的其實只有k1，k2兩個節點，三顆子樹沒有任何變化。

   另一種情況的單旋轉：

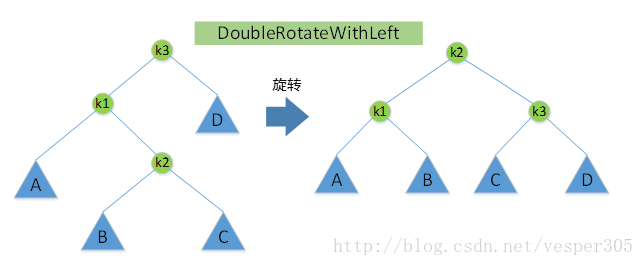
當對（2）a的左兒子的右子樹進行一次插入以及（3）對a的右兒子的左子樹進行一次插入的時候由於較深的子樹處於結構的中間，因此僅用單旋轉並不能解決問題，這個時候，我們必須分別在兩個節點之間使用兩次單旋轉，即一次雙旋轉使AVL樹重新恢復平衡。

我們觀察到，二叉樹的右邊可以對k1-k2兩個節點先進行一次SingleRotateWithLeft變換

然後把k1及其子樹看作是單旋轉中的第一種情況中的Z，然後這個時候對k3和k2之間進行一次SingleRotateWithRight變換即可達到平衡的目的。

上面的思路其實很簡單，將深度過深的樹從整棵樹的中間往邊上轉移，然後就可以參考單旋轉中的操作來解決不平衡的問題了。

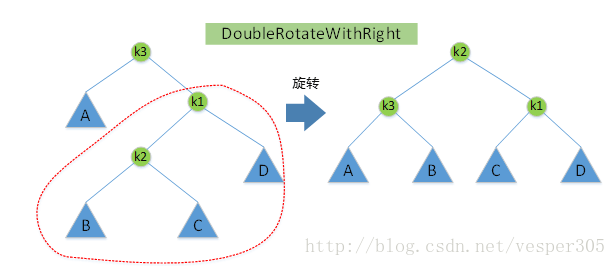
下面我們可以看到另一種情況的雙旋轉

2.2.旋轉操作中的本質

在上面的四種旋轉操作中我們可以看到，其實整個操作中發生變化的點很少，單旋轉中只有（k1 k2）兩個點，雙旋轉中只有（k1 k2）、（k3 k2）三個點，其餘的子樹只有父節點發生了變化，但是這與子樹本身沒有任何關係。

在具體的程式碼實現中我們應該注意，因為變化的只有兩個或是三個節點，因此旋轉操作之後更新高度只需要對這兩個或是三個節點更新。（雙旋轉操作中是分兩組更新的！）

3.具體實現程式碼

#include <stdio.h>
#include <stdlib.h>

#define Max( a , b ) ( (a) > (b) ? (a) : (b) )

typedef int ElementType;
struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;




struct AvlNode
{
	ElementType Element;
	AvlTree Left;
	AvlTree Right;

	int     Height;
};

static int Height( Position P )
{
	if ( P == NULL )
		return -1;
	else
		return P->Height;
}

/*This function can be called only if k2 has a left child*/
/*Perform a rotate between a node (k2) and its left child*/
/*Update heights , then return new root*/
static Position SingleRotateWithLeft( Position k2 )
{
	Position k1;

	k1 = k2->Left;
	k2->Left = k1->Right;
	k1->Right = k2;

	k2->Height = Max( Height( k2->Left) , Height( k2->Right ) ) + 1;
	k1->Height = Max( Height( k1->Left) , k2->Height ) + 1;

	return k1; //new root
}

static Position SingleRotateWithRight( Position k2 )
{
	Position k1;

	k1 = k2->Right;
	k2->Right = k1->Left;
	k1->Left = k2;

	k2->Height = Max( Height( k2->Left ) , Height( k2->Right ) ) + 1;
	k1->Height = Max( Height( k1->Right ) , k2->Height ) + 1;

	return k1;
}

/*This function can be called only if k3 has a left*/
/*child and k3's left child has a right child*/
/*Do the left-right double rotation*/
/*Update heights,then return new root*/
static Position DoubleRotateWithLeft( Position k3 )
{
	/*Rotate between k1 and k2*/
	k3->Left = SingleRotateWithRight( k3->Left );

	/*Rotate between k3 and k2*/
	return SingleRotateWithLeft( k3 );
}

static Position DoubleRotateWithRight( Position k3 )
{
	/*Rotate between k1 and k2*/
	k3->Right = SingleRotateWithLeft( k3->Right );

	/*Rotate between k3 and k2*/
	return SingleRotateWithRight( k3 );
}


AvlTree Insert( ElementType X , AvlTree T )
{
	if ( T == NULL )
	{
		/*Create and return a one-node tree */
		T = ( AvlTree )malloc (sizeof( struct AvlNode ));
		if ( T == NULL )
			printf("Out of space!!!\n");
		else
		{
			T->Element = X ; T->Height = 0 ; //The height of the leef is 0 !!! Different from the normal tree!
			T->Left = T->Right = NULL;
		}
	}
	else
		if ( X < T->Element )
		{
			T->Left = Insert ( X , T->Left );
			if( Height(T->Left) - Height( T->Right) == 2 )
				if ( X < T->Left->Element )
					T = SingleRotateWithLeft( T );
				else 
					T = DoubleRotateWithLeft( T );
		}
		else 
			if ( X > T->Element )
			{
				T->Right = Insert( X , T->Right );
				if( Height(T->Right) - Height(T->Left) == 2 )
					if( X > T->Right->Element )
						T = SingleRotateWithRight( T );
					else
						T = DoubleRotateWithRight( T );
			}
	/* Else X is in the tree already; we'll do nothing!*/

	T->Height = Max( Height( T->Left) , Height( T->Right ) ) + 1;
	return T;
}

AvlTree Init_AvlTree(AvlTree T, ElementType *ElementArry,int length)
{
	int i;
	//逐個插入查詢二叉樹中
	T->Element = ElementArry[0]; //在初始化的過程中直接把第一個點作為根節點。

	for(i=1;i<length;i++)
		Insert(ElementArry[i],T);

	return T;
}

int main(int argc, char const *argv[])
{
	// 初始化指標
	AvlTree T = ( AvlTree )malloc(sizeof( struct AvlNode ));
	T->Left = NULL;
	T->Right = NULL;

	Position Temp;

	ElementType ElementArry[11]= {15,6,18,3,7,17,20,2,4,13,9};

	/*Initialize the AvlTree*/
	T = Init_AvlTree( T , ElementArry , 11 );

	printf("%d\n", T->Left->Right->Left->Element );

	return 0;
}