ps 之前一直對卷積前後資料的尺寸變化的理解不是很清晰。現在藉著肺結節的專案自己重新整理一下。

1.二維上的卷積

沒錯還是這篇文章https://buptldy.github.io/2016/10/29/2016-10-29-deconv/ 真是好文。

## 卷積層

卷積層大家應該都很熟悉了,為了方便說明，定義如下：
- 二維的離散卷積（N=2N=2）
- 方形的特徵輸入（i1=i2=ii1=i2=i）
- 方形的卷積核尺寸（k1=k2=kk1=k2=k）
- 每個維度相同的步長（s1=s2=ss1=s2=s）
- 每個維度相同的padding (p1=p2=pp1=p2=p)

下圖表示引數為 (i=5,k=3,s=2,p=1)(i=5,k=3,s=2,p=1) 的卷積計算過程，從計算結果可以看出輸出特徵的尺寸為 (o1=o2=o=3)(o1=o2=o=3)。

下圖表示引數為 (i=6,k=3,s=2,p=1)(i=6,k=3,s=2,p=1) 的卷積計算過程，從計算結果可以看出輸出特徵的尺寸為 (o1=o2=o=3)(o1=o2=o=3)。

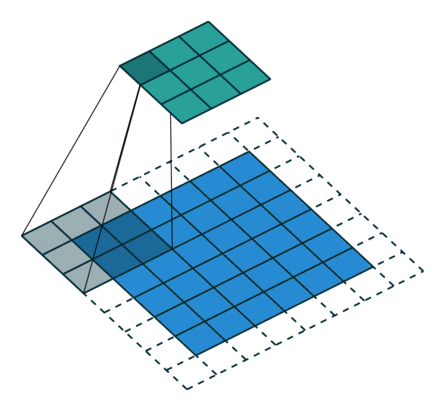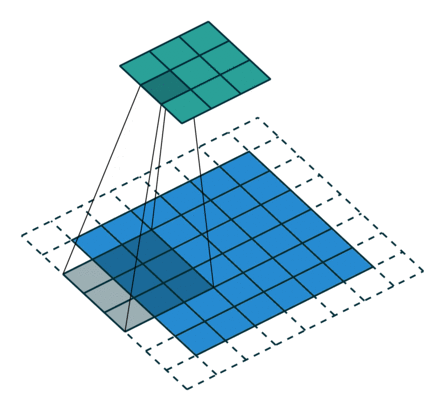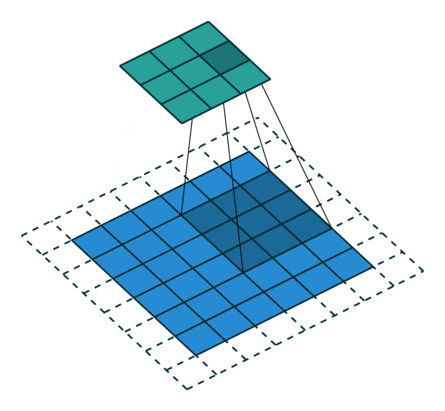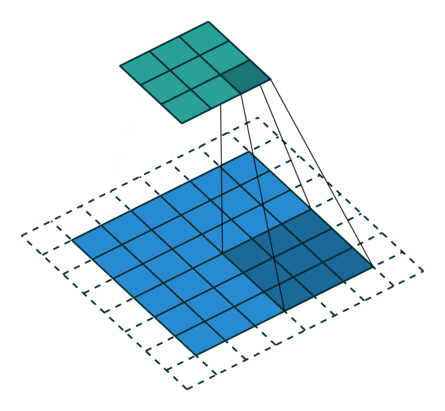
從上述兩個例子我們可以總結出卷積層輸入特徵與輸出特徵尺寸和卷積核引數的關係為：

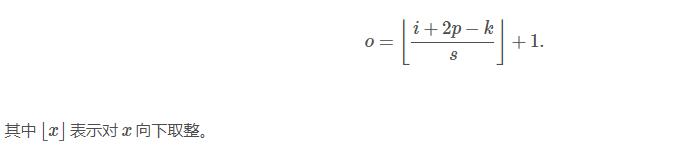
ps當然選擇same的模式就好（大小不變）

2.實際程式碼中卷積前後尺寸變化

這篇部落格中給出的解釋讓我印象深刻https://blog.csdn.net/loveliuzz/article/details/79135583

Inception架構的主要思想是找出如何用密整合分來近似最優的區域性稀疏結。（用的是same）

對上圖做以下說明： 

1 . 採用不同大小的卷積核意味著不同大小的感受野，最後拼接意味著不同尺度特徵的融合； 

2 . 之所以卷積核大小採用1*1、3*3和5*5，主要是為了方便對齊。設定卷積步長stride=1之後，

只要分別設定padding =0、1、2，採用same卷積可以得到相同維度的特徵，然後這些特徵直接拼接在一起； 

3 . 文章說很多地方都表明pooling挺有效，所以Inception裡面也嵌入了pooling。 

4 . 網路越到後面特徵越抽象，且每個特徵涉及的感受野也更大，隨著層數的增加，3x3和5x5卷積的比例也要增加。
 

ps 下面還有好多圖，我就不放了。這篇是很詳細的介紹了Inception V3的改進過程和程式碼實現，感興趣的可以去看看。其實我還是有點無法理解1*1的卷積和最大池化是怎麼實現這樣的尺寸變化的。

1*1的卷積

直到我看到這篇博文的這段話我才發現我對其它尺寸的卷積的理解其實一樣沒有透徹處在模稜兩可的狀態：https://blog.csdn.net/chaipp0607/article/details/60868689 （越簡單的東西才能看出其本質）

當1*1卷積出現時，在大多數情況下它作用是升/降特徵的維度，這裡的維度指的是通道數（厚度），而不改變圖片的寬和高。

舉個例子，比如某次卷積之後的結果是W*H*6的特徵，現在需要用1*1的卷積核將其降維成W*H*5，即6個通道變成5個通道。通過一次卷積操作，W*H*6將變為W*H*1，這樣的話，使用5個1*1的卷積核，顯然可以卷積出5個W*H*1，再做通道的串接操作，就實現了W*H*5。在這裡先計算一下引數數量，一遍後面說明，5個卷積核，每個卷積核的尺寸是1*1*6，也就是一種有30個引數。

我們還可以用另一種角度去理解1*1卷積，可以把它看成是一種全連線，如下圖： 

第一層有6個神經元，分別是a1—a6，通過全連線之後變成5個，分別是b1—b5，第一層的六個神經元要和後面五個實現全連線，本圖中只畫了a1—a6連線到b1的示意，可以看到，在全連線層b1其實是前面6個神經元的加權和，權對應的就是w1—w6，到這裡就很清晰了： 
第一層的6個神經元其實就相當於輸入特徵裡面那個通道數：6，而第二層的5個神經元相當於1*1卷積之後的新的特徵通道數：5。 
w1—w6是一個卷積核的權係數，如何要計算b2—b5，顯然還需要4個同樣尺寸的核。

最後一個問題，影象的一層相比於神經元還是有區別的，這在於是一個2D矩陣還是一個數字，但是即便是一個2D矩陣的話也還是隻需要一個引數（1*1的核），這就是因為引數的權值共享。

這解釋透徹有沒有。

推到3*3的卷積也是一樣的比如某次卷積之後的結果是W*H*6的特徵，極端一點現1個用3*3的卷積核將其卷積得到的不是W*H*6的特徵，而是W*H*1的特徵。相當於每個W*H的特徵與3*3卷積核卷積等到1個W*H的特徵，最後將這6個特徵對應位置相加取平均（猜測可能就是求和沒取平均)得到一個W*H*1的特徵計算結果。所以二維卷積最後一個通道數是由多少個卷積核決定的。

最大池化Inception架構圖中理解不了28*28*192同maxpool怎麼就成28*28*32。按之前的理解不應該還是28*28*192（步長1，same）。直到檢視Inception V3原始碼是想到可以是先從28*28*192池化到28*28*192在用1*1*32的卷積不久ok了。在回頭看其實作者在圖中已經提醒我們了-將28*28框了出來。像我這種小白只能事後諸葛亮了！

PS其實我最關心的部分是3d卷積以及實際計算中卷積計算前後尺寸變化，畢竟現在要做啊，這可能之後再寫吧。

12月25日新增

其實上面我自己的理解還有一定問題直到，我今天為了理解FPN去看目標檢測網路的發展時，看到的這篇博文https://www.cnblogs.com/skyfsm/p/6806246.html 才感覺這裡面有問題啊。然後專門去看了CNN卷積計算通道數前後變化，先找到了這篇博文https://blog.csdn.net/u014114990/article/details/51125776，而後這篇博文https://blog.csdn.net/dulingtingzi/article/details/79819513據上面的博文添加了在通道數變化問題更好理解的話如下：

多通道多個卷積核
下圖展示了在四個通道上的卷積操作，有兩個卷積核，生成兩個通道。其中需要注意的是，四個通道上每個通道對應一個2*2的卷積核，這4個2*2的卷積核上的引數是不一樣的，之所以說它是1個卷積核，是因為把它看成了一個4*2*2的卷積核，4代表一開始卷積的通道數，2*2是卷積核的尺寸，實際卷積的時候其實就是4個2*2的卷積核（這四個2*2的卷積核的引數是不同的）分別去卷積對應的4個通道，然後相加，再加上偏置b，注意b對於這四通道而言是共享的，所以b的個數是和最終的featuremap的個數相同的，先將w2忽略，只看w1，那麼在通道的某位置（i,j）處的值，是由四個通道上（i,j）處的卷積結果相加，再加上偏置b1，然後再取啟用函式值得到的。  所以最後得到兩個feature map， 即輸出層的卷積核個數為 feature map 的個數。也就是說卷積核的個數=最終的featuremap的個數，卷積核的大小=開始進行卷積的通道數*每個通道上進行卷積的二維卷積核的尺寸（此處就是4*（2*2）），b（偏置）的個數=卷積核的個數=featuremap的個數。

下圖中k代表featuremap的個數，W的大小是（4*2*2）

所以，在上圖由4個通道卷積得到2個通道的過程中，引數的數目為4×（2×2）×2+2個，其中4表示4個通道，第一個2*2表示卷積核的大小，第三個2表示featuremap個數，也就是生成的通道數，最後的2代表偏置b的個數。

現在再推到3*3的卷積，某次卷積之後的結果是W*H*6的特徵，接著極端一點現1個3*3的卷積核，但其實這個卷積核尺寸是6*3*3而不是3*3。我一直理解錯了，為什麼一般都沒有標註出前面這個六呢，其實是因為這個引數是有前面的層數決定的。

再推到1*1卷積，某次卷積之後的結果是W*H*6的特徵，接著極端一點現1個1*1的卷積核，但其實這個卷積核尺寸同樣是6*1*1而不是1*1。這就是相當於全連結啊。

ps12月26日新增，發現沒講最大池化。其實28*28*192同maxpool成28*28*32，其實其中也先是maxpool到28*28*192（步長1，same），接著用192*1*1*32卷積而非1*1*32卷積。只是不太清楚要不要加32個偏置b。

心得：發現自己困惑的地方一定要儘可能去明確它，解決它。這對之後修改別人的程式碼幫助很大。小白的理解希望對你有用。