一）區域性二值模式簡介

前面介紹過關於主成分分析法的識別方法，這個方法是選取的整幅影象的主成分分量來作為新的特徵，從某種意義上說這是一種基於全域性特徵的方法。但是一般影象識別中，僅僅使用全域性特徵是不夠的，獲得的識別率較低，更多的時候，表徵一副影象的特徵也缺少不了區域性特徵。那麼區域性二值模式（LBP）就是這樣一種表徵區域性特徵的方法。

介紹性原理的文章很多，這裡貼個較好的：

研究該演算法的過程中還發現了一篇較好的碩士論文：

基於LBP的人臉識別研究_黃非非

想深入瞭解的可以看看。

一）經典LBP特徵提取的程式實現

在介紹實現之前請一定要看上述的那篇部落格，那個裡面有相關的介紹原理，看了這個原理才能知道演算法的實現過程。這裡也是介紹經典的矩形3*3領域實現方法。

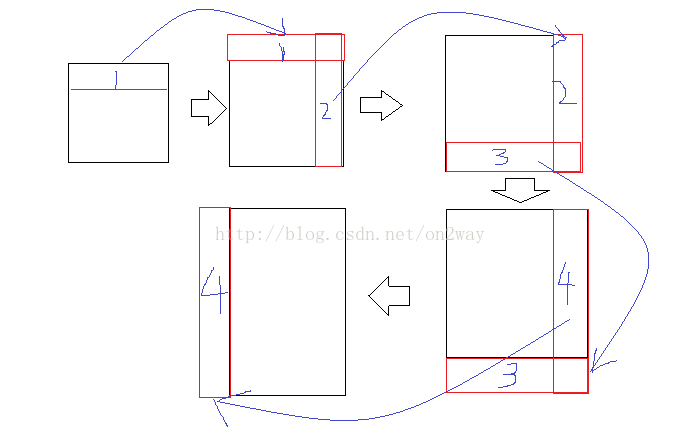
從上述原理可以知道，要得到影象中的每個畫素點的LBP值，必須和它的領域有關，所以它的四周必須得有畫素點，這就出現了一個問題，對於一個影象邊緣畫素點來說怎麼辦？它是邊緣點，那麼必定存在著它的3*3領域內的某幾個點超出影象之外，也就是沒有畫素值，這樣會出現錯誤的，那麼一個解決辦法就是對原影象進行畫素擴充套件，也就是把原影象的四周向外擴充套件一下，畫素點的灰度擴充套件成多少？可以是把邊界點的畫素複製過去就可以了（當然還有其他方法），知道影象濾波的可能會知道，在濾波演算法中也存在著邊界點的處理過程，本質上方法是一樣的。

考慮到是3*3的矩形領域，那麼四周邊界點只需要向外擴充套件一行或者一列就行了。如果矩形框改變大小，那麼向外擴充套件的大小也改變。簡單的擴充套件描述過程如下：

把相應的位置複製到新的擴充套件圖中就可以了。

從原理中看到某個畫素點的LBP值得計算公式可以簡單描述為：

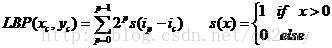
其中，2^p的係數可以用矩陣代替：C = [1,2,4;128,0,8;64,32,16];

求和可以用矩陣的點乘來代替並求和。矩陣點乘就是矩陣對應位置與對應位置相乘，和矩陣直接相乘還是有很大的區別。

有了上述分析，程式可以寫成如下：

%--------------函式說明-------------  
%-----LBP：Local Binary Patterns，區域性二值模式
%-----輸入:img原始灰度影象:注意圖片為double型
%-----輸出:該影象的的LBP特徵
%-----------------------------------  
function LBP = Lbp_Img(img)
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[m,n] = size(img);%取大小
r = 1;
img_extend = zeros(m+2*r,n+2*r);%規定擴充套件後的矩陣大小並賦值0
img_extend(r+1:m+r,r+1:n+r) = img;%中間部分複製
img_extend(1:r,r+1:n+r) = img(1:r,1:n);%上擴充套件
img_extend(1:m+r,n+r+1:n+2*r) = img_extend(1:m+r,n+1:n+r);%右擴充套件
img_extend(m+r+1:m+2*r,r+1:n+2*r) = img_extend(m+1:m+r,r+1:n+2*r);%下擴充套件
img_extend(1:m+2*r,1:r) = img_extend(1:m+2*r,r+1:r+1:2*r);%左擴充套件

%%
C = [1,2,4;128,0,8;64,32,16]; %矩陣點乘的權值矩陣
LBP = zeros(m,n);
for i=1:m   %對所有的畫素點
    for j=1:n
        temp = img(i,j);   %取得該點畫素值--也就是中心值
        temp_mat = ones(3)*temp;  %檢測得鄰域矩陣3*3
        temp_ext = img_extend(i+r-1:i+r+1,j+r-1:j+r+1);%取得鄰域矩陣畫素點
        temp_mean = temp_ext - temp_mat;  %相差
        temp_mean(find(temp_mean>=0)) = 1; %判斷，置0與1
        temp_mean(find(temp_mean<0)) = 0;
        LBP(i,j) = sum(sum(C.*temp_mean));   %點乘並求和返回LBP
    end
end
 

二）:樣本圖片的LBP提取與直方圖顯示：

現在對一副影象進行提取整個影象的LBP,很顯然一幅影象的LBP必定是與原影象相同大小的矩陣才對。現在我們隨意找來一副影象進行提取LBP：

首先轉化成灰度影象，並進行double型轉換，最後直接執行

LBP = Lbp_Img(img);imshow(LBP,[])

如下(注意imshow函式在顯示的時候加上[],使其自適應顯示，不然顯示不出來這個圖)：

LBP演算法的一大優點就是對光照具有較強的魯棒性，現在人為用matlab改變一下樣本的原始亮度，再顯示他們的LBP如下所示：

可以看到在亮度不同的條件下他們的LBP基本上沒有多大變化。

那麼怎麼去進行後續處理呢？一個很重要的處理方法就是對LBP進行灰度直方圖處理，在直方圖的基礎上進一步處理。

對上述得到的LBP，matlab本身自帶直方圖統計與顯示函式hist，但是它只能處理一行或者一列的資料，所以對LBP這種矩陣首先得進行處理成一行再來運用，這裡我們又可以運用reshape函數了。處理與顯示如下：

>> [m,n] = size(LBP);

data = reshape(LBP,1,m*n);

hist(data,255);

[nel,cen] = hist(data,255);

統計直方圖如下所示：

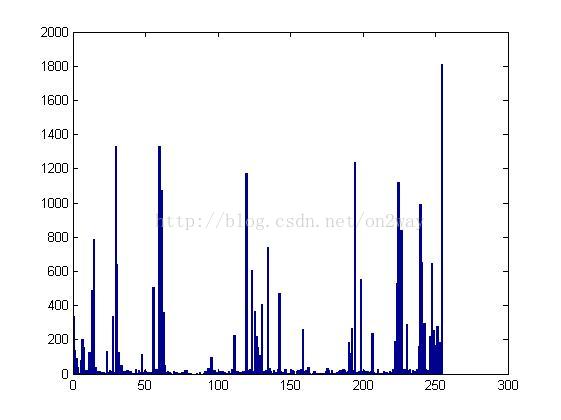
還有一個我們關心的數字就是上述的nel，這是每個畫素點的LBP中的總統計個數,而cen是中心點，其實就是1~255（所有灰度值）。nel這個1*n的資料在後面的處理時至關重要。