【影象特徵提取2】區域性二值模式LBP----從原理到實踐
阿新 • • 發佈：2018-12-31
(一)區域性二值模式LBP的簡介
LBP(Local Binary Pattern,區域性二值模式)是一種描述影象區域性紋理的特徵運算元，該運算元是由T.Ojala等人於1994年首次提出來的，後來經過改進，可用於影象特徵分析，該運算元具有旋轉不變性和灰度不變性等顯著的優點。 經過改進之後的區域性二值模式LBP特徵是高效的影象特徵分析方法， 已經應用於多個領域之中，特別是在人臉識別、表情識別、行人檢測、紋理分類等領域取得了成功。LBP特徵將視窗中心點與鄰域點的關係進行比較，重新編碼已形成新的特徵，這樣在一定程式上消除了外界場景對影象的影響，因此，在一定程度上解決了複雜場景下(光照變化)的特徵描述的問題（二）經典的LBP特徵設計
經典的LBP運算元定義為3*3的正方形視窗，以視窗的中心畫素為閾值，將其相鄰的8鄰域畫素的灰度值與當前視窗的中心點的畫素值進行比較，若鄰域的畫素值小於中心點的畫素值，則置該畫素點的值為0，反之，則置為1。這樣，一個3*3視窗的鄰域內的8個畫素點和中心畫素點進行比較之後，就會產生一個8位的二進位制數,即可產生256中LBP碼，通過這樣計算得到的LBP碼值就可以用來反映該視窗的區域紋理特徵資訊。如下圖所示: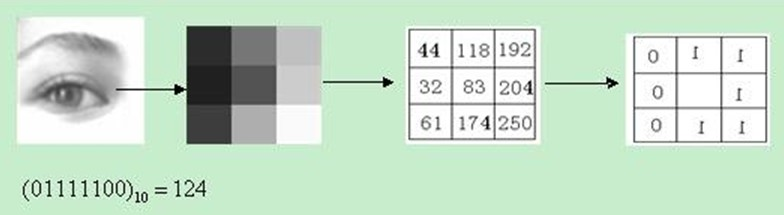
八位的二進位制陣列成LBP碼值的的規則是：在這個3*3的視窗內，沿著順時針開始組合成一個8位的二進位制數，然後轉換成10進位制數。 需要說明的是：區域性二值模式LBP特徵描述的是一種灰度範圍內的影象處理技術，針對的輸入影象是8位的灰度影象。經典的LBP特徵的缺點是無法區分視窗中中心點畫素的值到底是等於還是大於鄰域上畫素點的灰度值，後續的改進引入了LBP+和LBP-因子用來區分上述說的這個缺點。
1）灰度不變性
通常，同樣的物體具有同樣的紋理特徵，但是在不同時間段對物體的拍照會因為外界的光照變換，導致同樣物體不同時間段或者不同光照條件下的成像，亮度差異比較大。但是LBP具有灰度不變性的特徵，可以抑制光照變換所帶來的影響。 如下圖所示，第一幅圖想經過LBP變換後得到的LBP碼為11110001.而第二幅影象的每個畫素在第一幅影象的基礎上增加50，進行LBP變換後，得到的LBP碼值仍然是11110001.因此，LBP特徵反應了局部亮度的相對變化，所以整體上增加或者減少一個值對於LBP特徵沒有大的影響。因此得到結論:差分分佈對平均光強不敏感。 但是，需要說明的是:LBP特徵也僅僅實在一定程度上對於光照具有魯棒性；例如，陰影對於物體成像的影響，LBP就沒有很好的抵抗效能。
(三)圓形LBP
經典的LBP用3*3的正方形視窗的8鄰域來描述影象的區域性影象紋理特徵，其缺點就是難以滿足不同尺度和頻率的要求。Ojala等人對經典的LBP進行來改進，提出了將3*3的正方形視窗擴充套件到任意的圓形鄰域。如下圖所示，所謂圓形鄰域，只是取樣的點選擇不同於八鄰域。它是以中心畫素為圓心，以R為半徑畫圓，在圓的邊界商均勻的選取P個點作為取樣點。而後面的處理方法與前面的八鄰域LBP方法一致。
需要說明的是:由於圓形LBP取樣點在圓形邊界點上，那麼必然會導致部分計算出來的取樣點的座標不是整數，因此，在這裡就需要對得到的座標點畫素值進行處理，常用的方法就是最近鄰插值和雙線性插值。下圖是R=1(pixel)，P=8時的情況。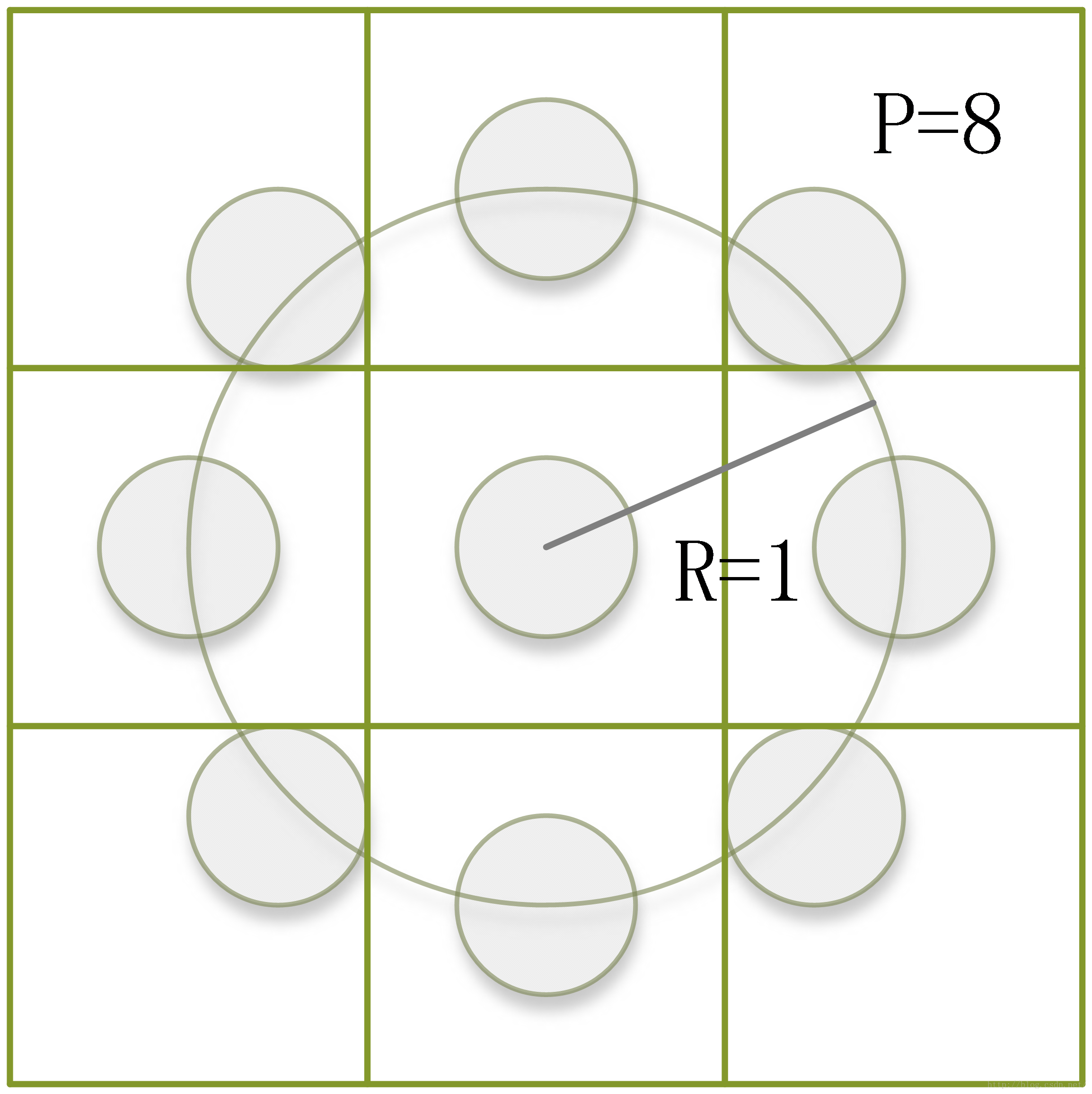
我們可以發
，R的大小就決定了圓的大小，反應了二維空間的尺度；而P的大小就決定了取樣點的點數，反應了角度空間的解析度。同樣，我們還可以通過改變R值和P值，實現不同的尺度和角度解析度(如下圖所示)。
1）旋轉不變性
對於下圖的兩個模式，其實只有方向不同，在實際中，是同一個模式的不同狀態，為了克服旋轉帶了的變化，引入了“旋轉不變性的概念”。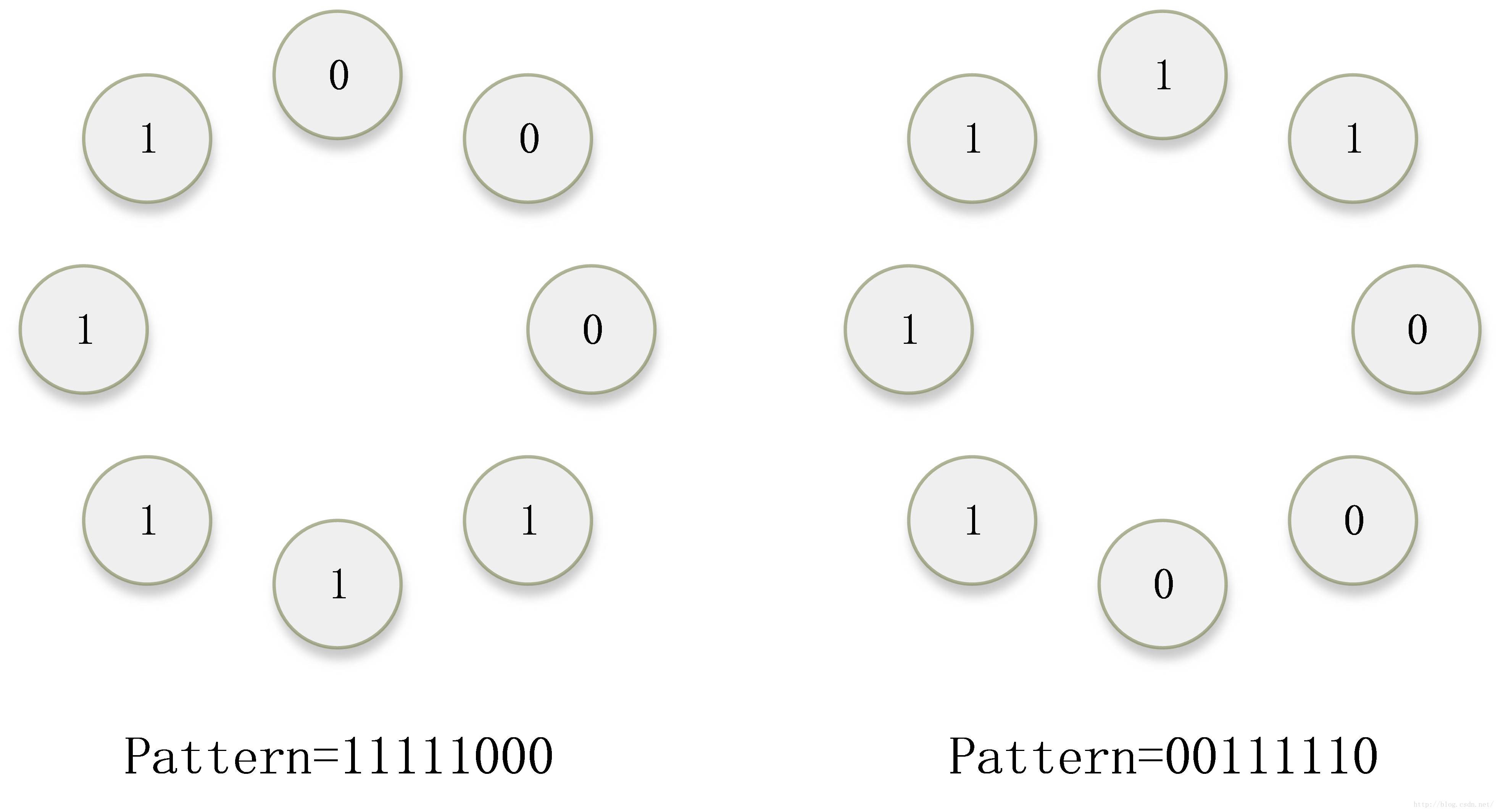
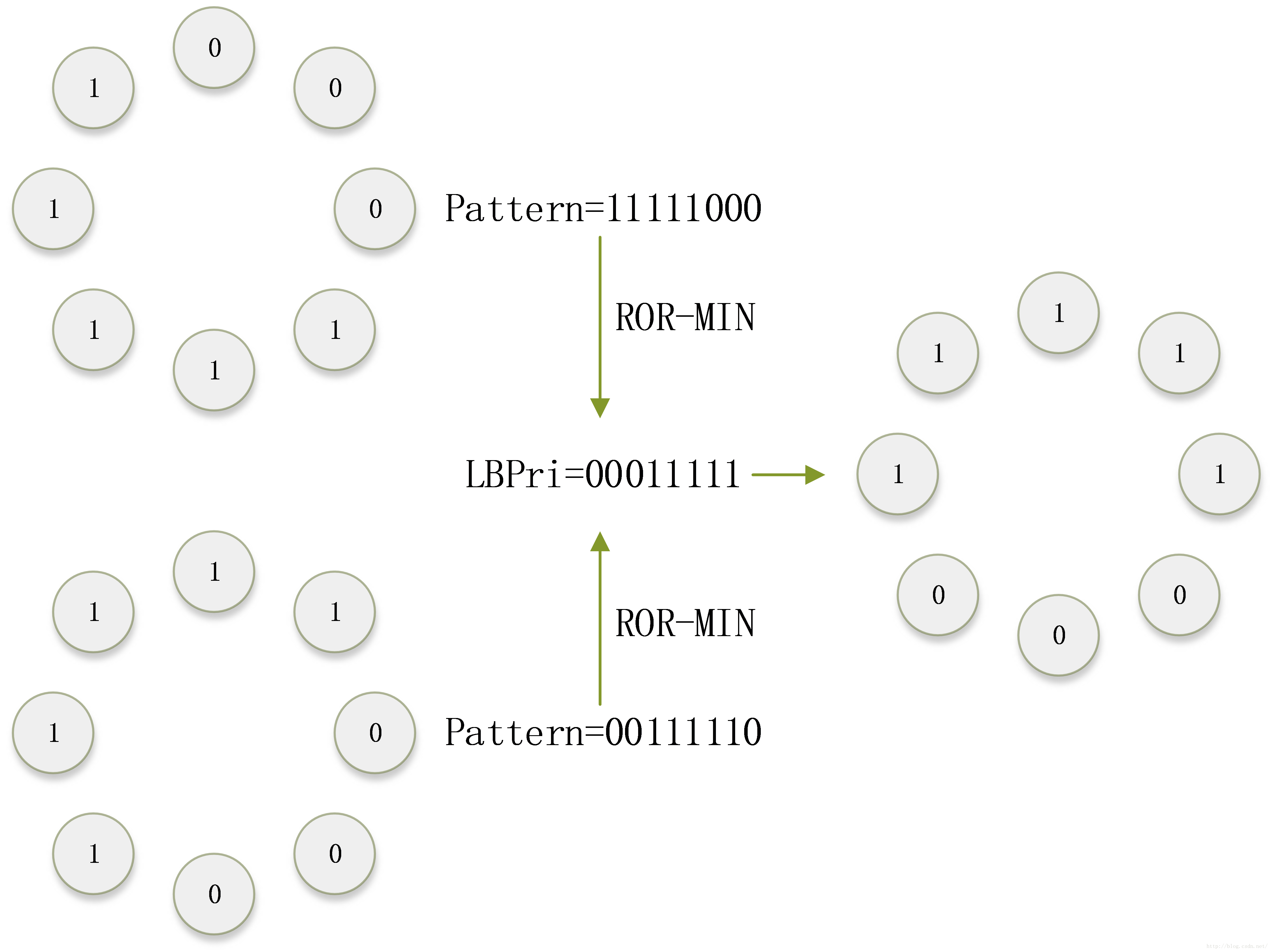
處理方法如下所示:兩種模式各有一個LBP值。將這個LBP值不斷的迴圈右移，並找到一個右移過程中最小的結果，作為新的LBP。可見，這兩種模式得到的新的LBP值相同，屬於同一種模式。以此解決方向變化的問題。其中，“迴圈右移”的實質是對模式圖案不斷的旋轉。“最小化”的過程的實質是“尋找能量最低的位置”。
對P=8的LBP，一共有8個取樣點，每個取樣點可能輸出0或者1，所以一共有256種區域性二值模式。其中一些僅僅是方向不同，通過旋轉之後就可以重合。通過以上的旋轉不變性處理之後，256種LBP變味了具有"旋轉不變性"的36種模式。如下圖所示:特點是，任意兩種模式經過任意旋轉之後不會重合。
2）增強型旋轉不變性
在實際應用中，我們通過統計就會發現，上圖中第一行的九種模式最為常見，而後面的27中模式並不常見，如果將後面的27種模式單獨歸類的話，會因為它們出現的概率太小，而具有一定的隨機性，因此，分類結果反而不穩定。因此。我們對這種方法進行了改進。 我們對每個LBP上的數值按順序讀一圈，將0->1和1->0的變化次數記為U。對於上圖可以發現,第一行模式的U值均小於2(反映了平坦或者變換區域)，而後面的27中模式的U值大於等於4(變化劇烈，不常見)。如下圖所示。這樣對於一般的LBP進行處理時，我們將U值小於等於2LBP每個單獨跟為一類，而對於U值大於4的LBP全部歸為一類。在P=8的情況下，原先分好的36類就變為現在的10類。
3）LBP特徵直方圖
我們以橫座標X表示LBP的類別，縱座標Y表示這一類別上的LBP特徵的個數，這樣我們將會得到一個LBP的特徵直方圖。如下圖所示。
參考的資料:
2)http://blog.csdn.net/u013207865/article/details/49720509