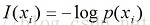機器學習之決策樹 機器學習之K-近鄰演算法
都說萬事開頭難,可一旦開頭,就是全新的狀態,就有可能收穫自己未曾預料到的成果。從2018.12.28開始,決定跟隨《機器學習實戰》的腳步開始其征程,記錄是為了更好的監督、理解和推進,學習過程中用到的資料集和程式碼都將上傳到github
機器學習系列部落格:(1) 機器學習之K-近鄰演算法
1. 什麼是決策樹
用闡述性的語言來說,決策樹通過對給出的學習樣本進行學習,自行產生出一個樹結構,每個葉節點都對應一簇資料,這一簇資料導向的結果是相同的;之後,將該樹結構抽離出來,對所需要進行分類並預測結果的資料進行分類,並預測其結果。
(1)決策樹在本質上就是一組巢狀的if-else判斷規則,看下圖:
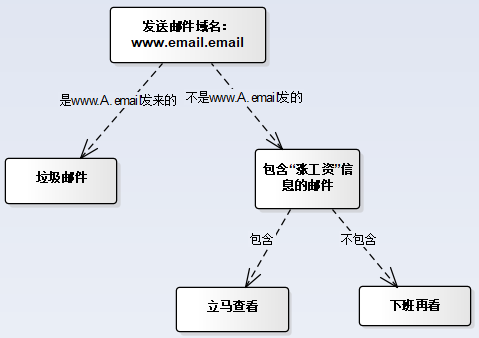
a. 首先根據判斷是不是www.A.email發來的郵件判斷是否為垃圾郵件
b. 再根據是否含漲工資資訊來判斷是不是要立馬檢視或下班再看
(2)決策樹能做什麼
有了上圖的決策樹後,下次再收到郵件,就可以將郵件交給這棵決策樹,立馬知道該如何對郵件進行處理
2. 溫習幾個重要概念
在建立決策樹之前,先來溫習下面的幾個重要的概念
(1)自資訊
對於自資訊的理解是學習決策樹的基礎之基礎,下面的內容務必理解!
以下內容摘抄自https://blog.csdn.net/xuejianbest/article/details/80391191,感謝博主的分享,很直接明瞭的解釋了資訊公式:
有時候我們會說“資訊量好大”,但是究竟怎麼比較資訊量的大小呢?我們需要量化資訊量的值。
舉個例子,你扔一個骰子,我不知道點數,你知道並告訴我。
你說"點數不大於6",這句話的資訊量應該等於0,因為我猜都猜的到,點數不大於6的概率是1,這句話沒有帶給我任何資訊;
你說 "點數不大於5",這句話的資訊量應該大於0,但是並不大,因為我猜能差不多猜的到,點數不大於5的概率是5/6 ,這句話帶給我的資訊較少;
你說 "點數為3",這句話的資訊量應該大於0,而且應比上面那句話資訊量大,因為"點數為3"包含了"點數不大於5"的資訊在裡面,點數為3的概率是1/6,這句話帶給我的資訊較多。
所以我們可以做出總結:資訊量的值和事件發生的概率有關係,概念越小資訊量越大,我們考慮用概率的相反數來量化資訊量,但是根據直覺,資訊量不應該為負數,所以我們考慮用概率的倒數來量化資訊量,設事件A發生的概念為p,則事件A發生了帶給我們的資訊量為1/p
考慮來考慮去,資訊量還應該有一個性質,就是可加性
再舉個例子:
情況一: 你扔了第一個骰子,告訴我"點數是3";
你扔了第二個骰子,告訴我"點數是1"。
那你兩次告訴我的總資訊量應該是第一次告訴我的資訊量加第二次告訴我的資訊量的和。
情況二: 你扔了第一個骰子,什麼都沒說;
你扔了第二個骰子,告訴我第一次點數是3,第二次點數是1。
根據直覺,這句話的資訊量應該和情況一中兩句話的資訊量的和一樣。
根據我們上面資訊量的量化公式算一下:
"點數是3"的概率為1/6,資訊量為6,"點數是1"的概率為1/6 ,資訊量為6,兩句話資訊量的和為12
第一次"點數是3",第二次"點數是1"的概率為(1/6)*(1/6)=1/36,資訊量為36
算出來的資訊量並不相等!所以我們要修正我們資訊量的量化公式,我們用函式I來修正原來資訊量等於概率的倒數的量化公式:設事件A發生的概率為p,則事件A發生了帶給我們的資訊量為I(1/p)。
兩次獨立事件A,B發生的概率分別為p1和p2,A和B同時發生概率為p1*p2,如上面所討論,資訊量的性質要求:

看出來沒,函式I的運算規則正好和對數的運算規則相同:
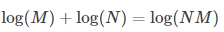
所以我們的函式可以用對數函式,最終我們給出資訊量的量化公式:設事件A發生的概率為p,則事件A發生了帶給我們的資訊量為logb(1/p),式中的b是對數的底,b的取值決定資訊量的單位,如b取2資訊量的單位是bit,b取自然常數e資訊量的單位是nat,容易計算1 nat=log2e≈1.443 bit1 nat=log2e≈1.443 bit
(2)期望
概率論中描述一個隨機事件中的隨機變數的平均值的大小可以用數學期望這個概念,數學期望的定義是實驗中可能的結果的概率乘以其結果的總和
舉個簡單的例子:
小時候玩的自動吐硬幣的賭博機,硬幣Y遵從以下概率分佈,吐0個幣的概率為0.7,吐10個幣的概率為0.29,吐20個幣的概率為0.01,那麼Y的期望值為:
E[Y] = 0*0.7 + 10 * 0.29 + 20 * 0.01
(3)熵
熵很難理解,拿書本上的一句話說,它們自從誕生的那一天起,就註定令世人十分費解。但是隻要記住熵定義為資訊的期望值,理解資訊和期望後,使用熵也就不費解了
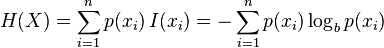
(4)資訊增量
Gain(S,Sv) = H(S)- (|Sv|/|S|)H(Sv)
資訊增益 = 經驗熵 - 條件熵
用通俗的話理解就是,當加入了一個判斷條件之後,我需要判定一個結論所需要的資訊熵相比之前就有所減少了,這減少的量就是資訊增益
3. 決策樹構造實現
3.1 需求
比如在海洋中有5種生物,我們根據(不浮出水面是否可以生存,是否有腳蹼(魚尾中間的薄膜))兩個分類特徵來判斷該生物是否屬於魚類來構建決策樹
看下錶:
| 浮出水面是否可以生存 | 是否有腳蹼 | 屬於魚類 | |
| 1 | 否 | 是 | 是 |
| 2 | 否 | 是 | 是 |
| 3 | 否 | 否 | 否 |
| 4 | 是 | 是 | 否 |
| 5 | 是 | 是 | 否 |
3.2 構思
(1)虛擬碼的建立
前面說決策樹在本質上就是一組巢狀的if-else判斷規則樹,那麼我有個疑惑:面對這麼多規則,我該先選哪個規則作為第一規則,再選哪個作為第二規則呢?規則選擇次序不同,對決策樹的構造會有什麼影響?
這兩個問題就涉及到了自資訊的概念,一個規則給我們提供的資訊量究竟有多大,資訊量越大我們肯定能最快的得到想要的答案,從而決策樹的高度也會最大程度的小
由此,我們首先需要判斷資料集上的哪個規則在劃分資料分類時起決定性作用,然後再對資料集進行劃分,建立分支的虛擬碼如下:
if so return 類標籤 else 尋找到分類資料種的最好特徵 劃分資料集 建立分支節點 for 每個劃分的子集 遞迴 return 分支節點
(2)找到資料集中的決定性特徵
我們可以計算每個特徵值劃分資料集獲得的資訊增益,獲得資訊增益最高的特徵就是最好的選擇
比如,先計算浮出水面是否可以生存的資訊增量gain(A),再計算是否有腳蹼的資訊增量gain(B),比較gain(A)和gain(B),哪個大就以哪個作為決定性特徵
3.3 實現
(1)計算資料集熵
熵為自資訊的期望,參照上面的定義
def calc_entropy(dataset): """ 計算熵,dataset為list """ rows = len(dataset) label_count = {} entropy = 0 for i in range(rows): label = dataset[i][-1] label_count[label] = label_count.get(label,0) + 1 for key,val in label_count.items(): p = val / rows l = log(p,2) * (-1) entropy += p*l return entropy
(2)選取最佳特徵
根據最大資訊增量,選取最佳特徵,遍歷每個特徵,計算其熵,然後與其原始資料集熵的差值來決定最大資訊增量,最大資訊增量時對應的特徵極為最佳特徵
def split_dataset_by_feature_value(dataset, feature_index, value): """ 根據給定特徵及其對應的特徵值拆分資料集 dataset:原始資料集 feature_index:特徵索引,也就是dataset的列索引 value:feature_index對應的特徵值 """ new_dataset = [] for row in dataset: if row[feature_index] == value: row_list = row[:feature_index] row_list.extend(row[feature_index+1:]) new_dataset.append(row_list) return new_dataset def choose_best_feature(dataset): """ 根據資訊增量,選擇最佳分類特徵 """ base_entropy = calc_entropy(dataset) feature_num = len(dataset[0]) - 1 #特徵個數 max_info_gain = 0 #資訊增量 best_feature = -1 #最佳特徵 for feature_index in range(feature_num): feature_value_list = [row[feature_index] for row in dataset] #特徵值列表 feature_value_set = set(feature_value_list) #特徵值集合,確保沒有重複值 new_entropy_sum = 0 #根據特徵分類後的熵和 info_gain = 0 for value in feature_value_set: sub_dataset = split_dataset_by_feature_value(dataset, feature_index, value) #根據特定特徵及其特徵值得到子資料集 prob = len(sub_dataset) / len(dataset) new_entropy = calc_entropy(sub_dataset) new_entropy_sum += prob * new_entropy info_gain = base_entropy - new_entropy_sum #計算資訊增量 if info_gain > max_info_gain: max_info_gain = info_gain best_feature = feature_index return best_feature
(3)構建決策樹
參照上面的虛擬碼
def max_count(classlist): """ 返回出現次數最多的類別 """ dic = {} for i in classlist: dic[classlist[i]] = dic.get(classlist[i],0)+1 sorted_list = sorted(dic.items(), key=lambda x: x[1], reserver=True) print('sorted_list:',sorted_list) return sorted_list[0][0] def create_policy_tree(dataset,lables): """ 構建決策樹 """ classlist = [example[-1] for example in dataset] if classlist.count(classlist[0]) == len(classlist): #類別完全相同停止繼續分類 return classlist[0] if len(dataset[0]) == 1: #遍歷完所有特徵時返回出現次數最多的類別 return max_count(classlist) best_feature = choose_best_feature(dataset) best_feature_lable = lables[best_feature] tree = {best_feature_lable:{}} del lables[best_feature] feature_value_list = [row[best_feature] for row in dataset] #特徵值列表 feature_value_set = set(feature_value_list) #特徵值集合,確保沒有重複值 for value in feature_value_set: sub_dataset = split_dataset_by_feature_value(dataset, best_feature, value) #根據特定特徵及其特徵值得到子資料集 tree[best_feature_lable][value] = create_policy_tree(sub_dataset,lables) return tree
注意:遞迴的條件就是不停的選擇最佳特徵並拆分資料集,遞迴基線條件有兩個:a. 類別完全相同停止繼續分類;b. 遍歷完所有特徵時返回出現次數最多的類別
(4)測試
if __name__ == '__main__': dataset = [[0,1,1],[0,1,1],[0,0,0],[1,1,0],[1,1,0]] lables = ['no surfacing','flippers'] print("policy tree:",create_policy_tree(dataset,lables))
輸出:

用matplotlib顯示如下:
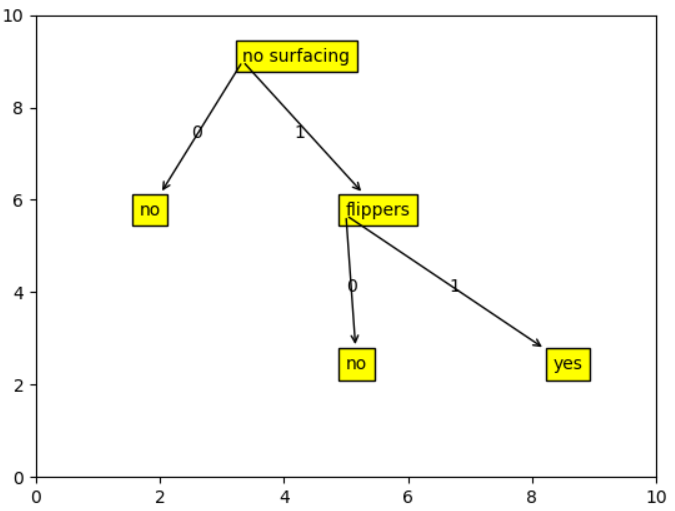
4. 總結
決策樹分類器就像帶有終止塊的流程圖,終止塊表示分類結果。開始處理資料時,首先需要測量集合資料的不一致性,也就是熵,然後尋找最優方案劃分資料集,直到資料集中的所有資料屬於同一分類。
k~近鄰演算法可以完成很多分類任務,但是它最大的缺點就是無法給出資料的內在含義,決策樹的主要優勢就在於資料形式非常容易理解
優點:計算複雜度不高,輸出結果易於理解,對中間值的缺失不敏感,可以處理不相關特徵的資料
缺點:可能會產生過度匹配問題