[三]機器學習之決策樹與隨機森林
3.1 目標任務
1.學習決策樹和隨機森林的原理、特性
2.學習編寫構造決策樹的python程式碼
3.學習使用sklearn訓練決策樹和隨機森林,並使用工具進行決策樹視覺化
3.2 實驗資料
資料集:鳶尾花資料集,詳情見[機器學習之迴歸]的Logistic迴歸實驗
3.3 決策樹特性和使用
3.3.1 決策樹的特性
決策樹(Decision Tree)是一種簡單但廣泛使用的分類器,通過訓練資料建立決策樹,可以高效地對未知資料進行分類。決策樹有兩大優點:
(1)決策樹模型可讀性好,具有描述性,有助於人工分析
(2)效率高,決策樹只需要一次構建,反覆使用,每一次預測的最大計算次數不能超過決策樹的深度
決策樹優點:計算複雜度不高,輸出結果易於理解,對中間值的缺失不敏感,可以處理不相關的特徵資料。
缺點:可能產生過度匹配問題(過擬合)
整體思路:大原則是“將無序資料變得更加有序”。從當前可供學習的資料集中,選擇一個特徵,根據這個特徵劃分出來的資料分類,可以獲得最高的資訊增益(在劃分資料集前後資訊發生的變化)。資訊增益是熵的減少,或者是資料無序度的減少。在劃分之後,對劃分出的各個分類再次進行演算法,直到所有分類中均為同一類元素,或所有特徵均已使用。
3.3.2 sk-learn中決策樹的使用
sklearn中提供了決策樹的相關方法,即DecisionTreeClassifier分類器,它能夠對資料進行多分類,具體定義及部分引數詳細含義如下表所示,詳細可檢視專案主頁(
| sklearn.tree.DecisionTreeClassifier class?sklearn.tree.DecisionTreeClassifier(criterion=’gini’,?splitter=’best’,?max_depth=None,?min_samples_split=2,?min_samples_leaf=1,?min_weight_fraction_leaf=0.0,?max_features=None,?random_state=None,?max_leaf_nodes=None,?min_impurity_decrease=0.0,?min_impurity_split=None,?class_weight=None,?presort=False) | ||
| 引數說明 | criterion:string | 衡量分類的質量。支援的標準有"gini"(預設)代表的是Gini impurity與"entropy"代表的是information gain |
| splitter:string | 一種在節點中選擇分類的策略。支援的策略有"best"(預設)選擇最好的分類和"random"選擇最好的隨機分類 | |
| max_depth:int or None | 樹的最大深度。如果是"None"(預設),則節點會一直擴充套件直到所有葉子都是純的或者所有的葉子節點都包含少於min_sample_split個樣本點。忽視max_leaf_nodes是不是為Node。 | |
| persort:bool | 是否預分類資料以加速訓練時最好分類的查詢。在有大資料集的決策樹中,如果設為true可能會減慢訓練的過程。當使用一個小資料集或者一個深度受限的決策樹中,可以減速訓練的過程。預設False | |
和其他分類器一樣,DecisionTreeClassifier有兩個向量輸入:X,稀疏或密集,大小為[n_sample,n_feature],存放訓練樣本;Y,值為整型,大小為[n_sample],存放訓練樣本的分類標籤。但由於DecisionTreeClassifier不支援文字屬性和文字標籤,因此需要將原始資料集中的文字標籤轉化為數字標籤,及X、Y應為數字矩陣。接著將X,Y傳給fit()函式進行訓練,得到的模型即可對樣本進行預測
from sklearn import tree
X = [[0,0],[1,1]]
Y = [0,1]
#初始化
clf = tree.DecisionTreeClassifier()
#根據XY資料訓練決策樹
clf = clf.fit(X,Y)
#根據訓練出的模型訓練樣本
clf.predict([[2.,2.]])隨機森林(Random Forest)
隨機森林指的是利用多棵樹對樣本進行訓練並預測的一種分類器。它通過對資料集中的子樣本進行訓練,從而得到多顆決策樹,以提高預測的準確性並控制在單棵決策樹中極易出現的過於擬合的情況。
sklearn中提供了隨機森林的相關方法,即RandomForestClassifier分類器,它能夠對資料進行多分類,聚體定義及部分引數詳細含義如下表所示,其中很多引數都與決策樹中的引數相似(頁面地址:http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html)。
| class sklearn.ensemble.RandomForestClassifier(n_estimators=’warn’, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None) | ||
| 引數說明 | n_estimators:integer | 隨機森林中的決策樹的棵樹,預設為0 |
| bootstrap:boolean | 在訓練決策樹的過程中是否使用bootstrap抽樣方法,預設為True | |
| max_depth:int or None | 樹的最大深度。如果是"None"(預設),則節點會一直擴充套件直到所有葉子都是純的或者所有的葉子節點都包含少於min_sample_split個樣本點。忽視max_leaf_nodes是不是為Node。 | |
| criterion:string | 衡量分類的質量。支援的標準有"gini"(預設)代表的是Gini impurity與"entropy"代表的是information gain | |
同樣,RandomForestClassifier有兩個向量輸入:X,稀疏或密集,大小為[n_sample,n_feature],存放訓練樣本;Y,值為整型,大小為[n_sample],存放訓練樣本的分類標籤。接著將X,Y傳給fit()函式進行訓練,得到的模型即可對樣本進行預測
3.4 實驗過程
3.4.1 實驗準備
(1)確保Numpy、Matplotlib和sklearn等庫已經正確安裝
(2)安裝graphivz工具,便於檢視決策樹結構(讀取dot指令碼寫成的文字檔案,做圖形化顯示)。Graphviz是一個開源的圖形視覺化軟體,用於表達有向圖、無向圖的連線關係,它在計算機網路、生物資訊、軟體工程、資料庫和網頁設計、機器學習燈諸多領域都被技術人員廣泛使用。下載地址:http://www.graphviz.org/download/
3.4.2 程式碼實現
(一)使用sklearn的決策樹做分類
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,:2]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#儲存
f = open("iris_tree.dot","w")
tree.export_graphviz(dt_clf,out_file=f)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[0])
plt.ylabel(iris_feature[1])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
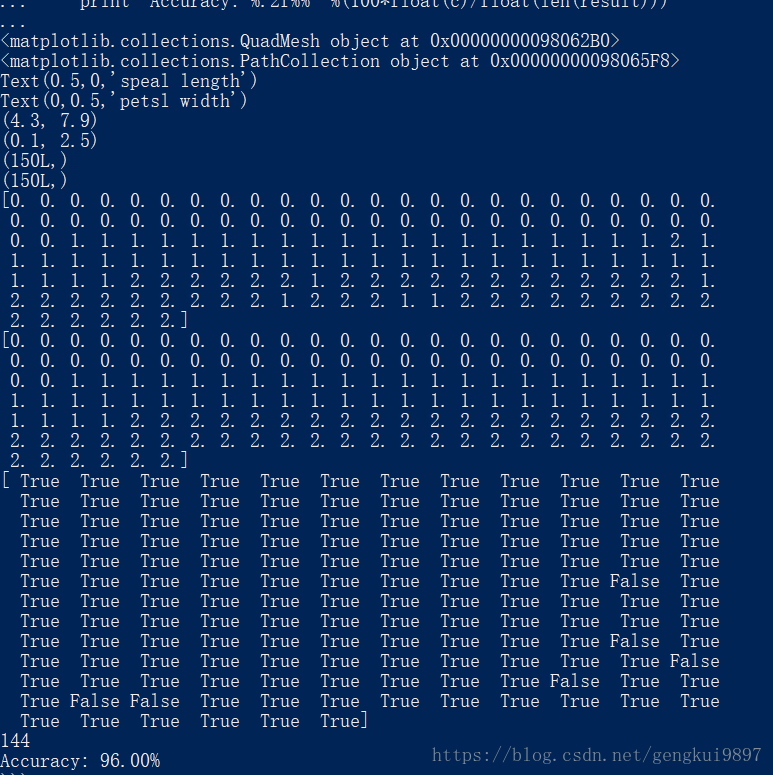
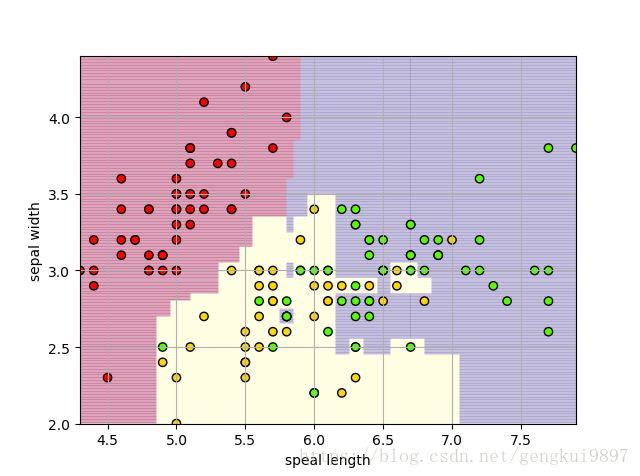
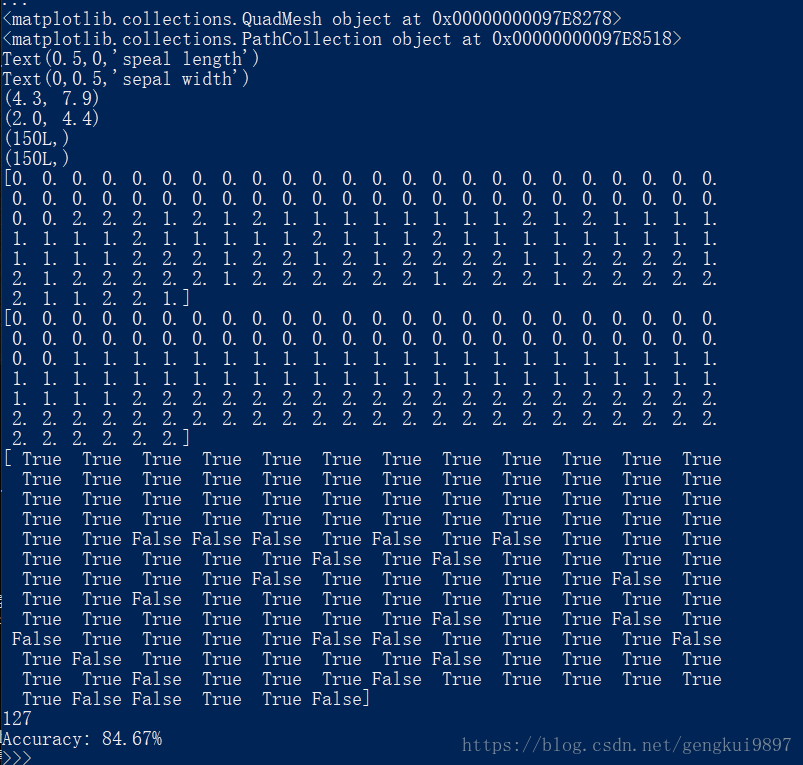
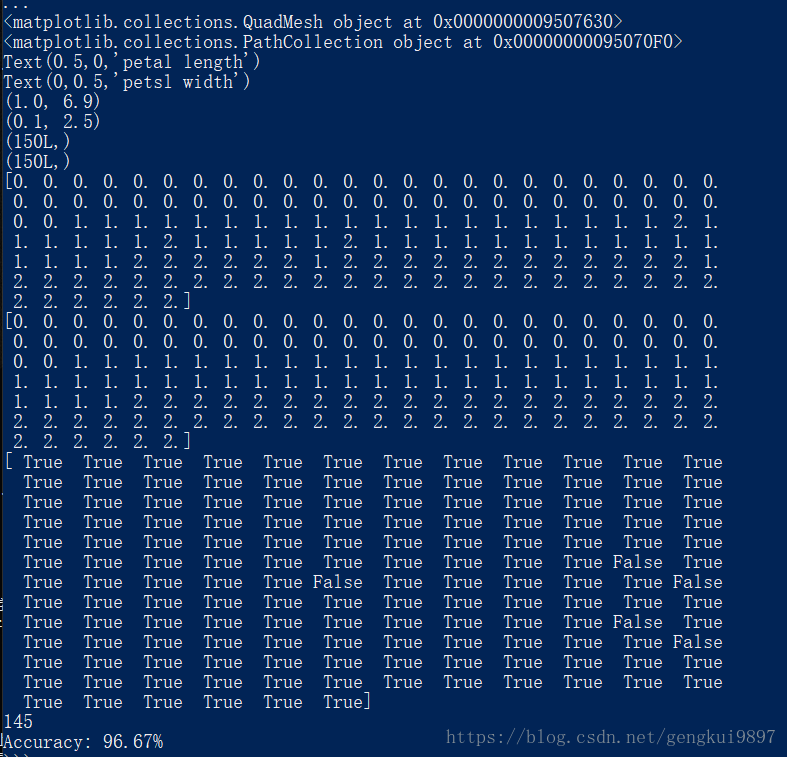
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))實驗結果:
結果分析:
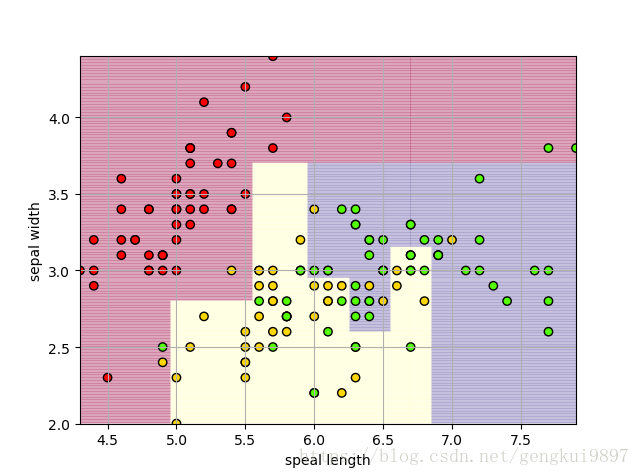
1.僅僅使用兩個特徵:花萼長度和花萼寬度,在150個樣本中,有123個分類正確,正確率為82%。
2.使用不同特徵、隨機森林進行實驗如下
兩特徵決策樹:
(1)花萼長度與花瓣長度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,::2]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#儲存
f = open("iris_tree.dot","w")
tree.export_graphviz(dt_clf,out_file=f)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[0])
plt.ylabel(iris_feature[2])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(2)花萼長度與花瓣寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,::3]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#儲存
f = open("iris_tree.dot","w")
tree.export_graphviz(dt_clf,out_file=f)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[0])
plt.ylabel(iris_feature[3])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
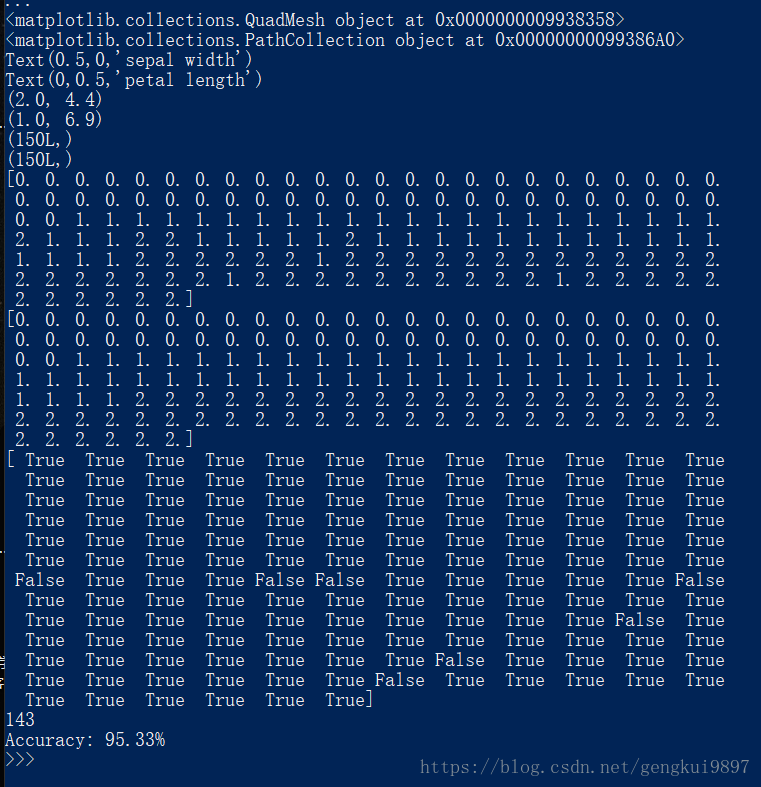
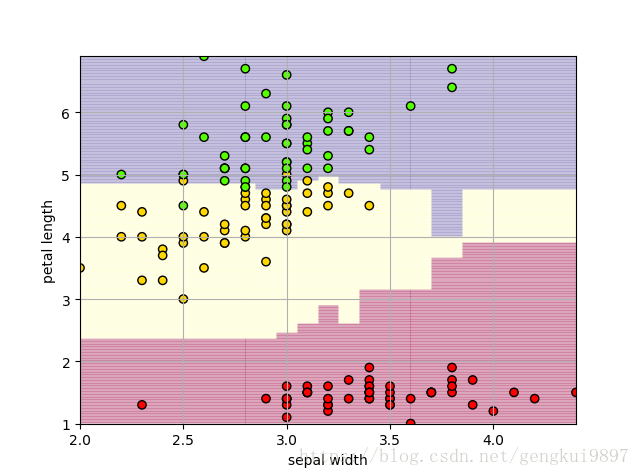
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(3)花萼寬度與花瓣長度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,1:3]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#儲存
f = open("iris_tree.dot","w")
tree.export_graphviz(dt_clf,out_file=f)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[1])
plt.ylabel(iris_feature[2])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
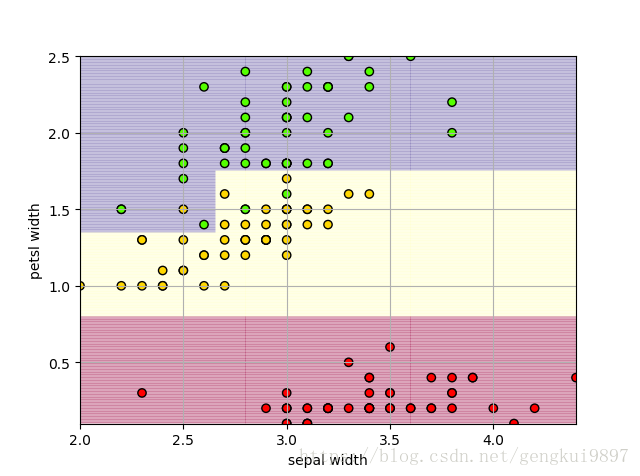
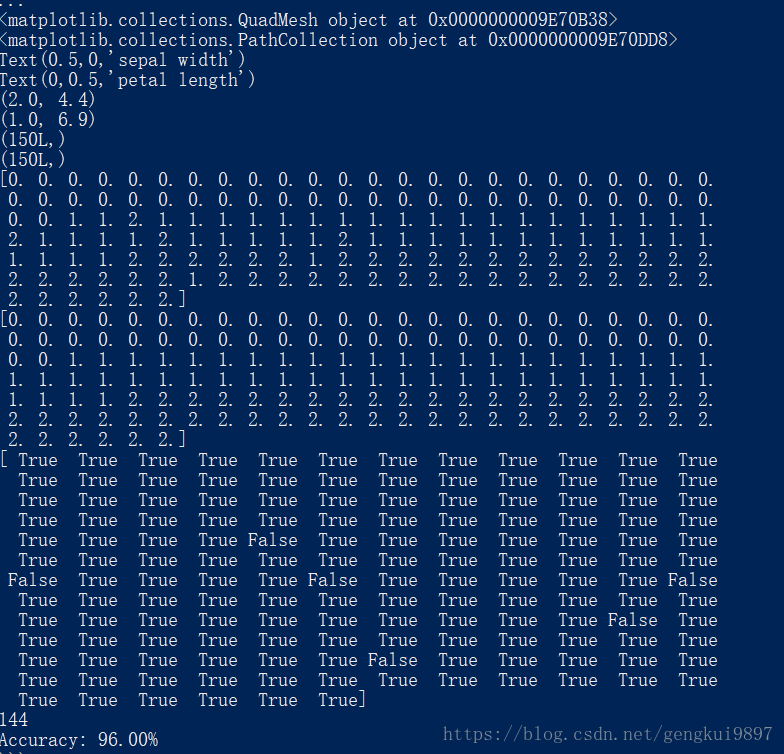
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(4)花萼寬度與花瓣寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,1::2]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#儲存
f = open("iris_tree.dot","w")
tree.export_graphviz(dt_clf,out_file=f)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[1])
plt.ylabel(iris_feature[3])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
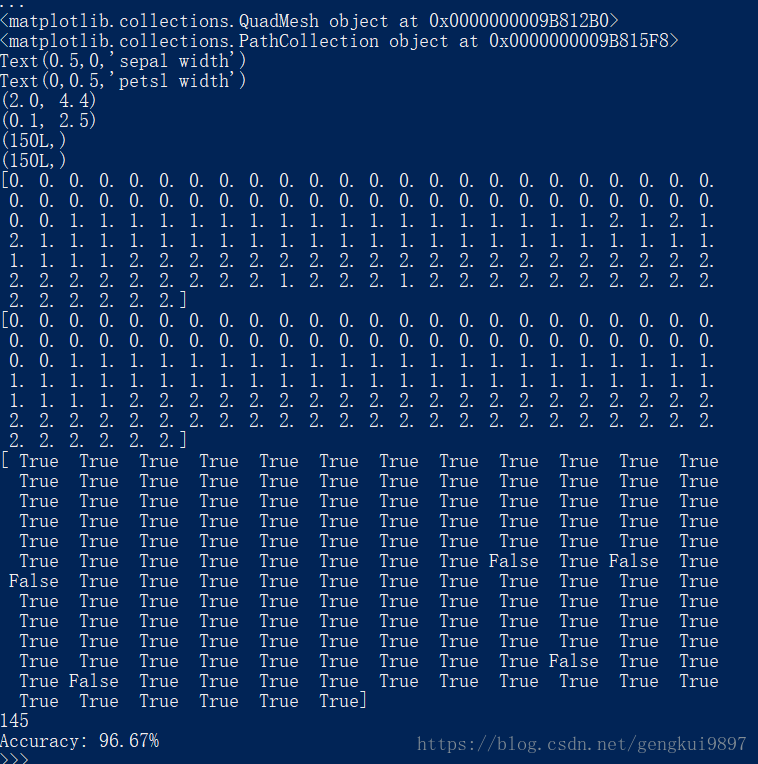
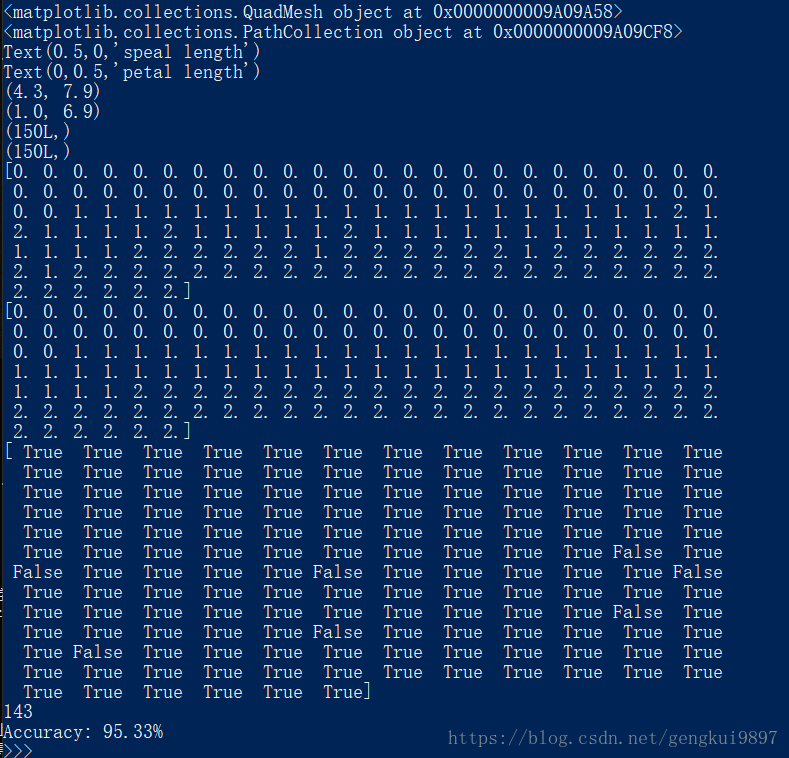
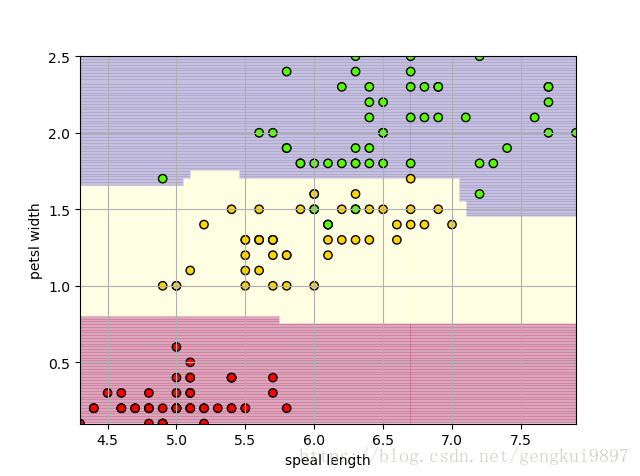
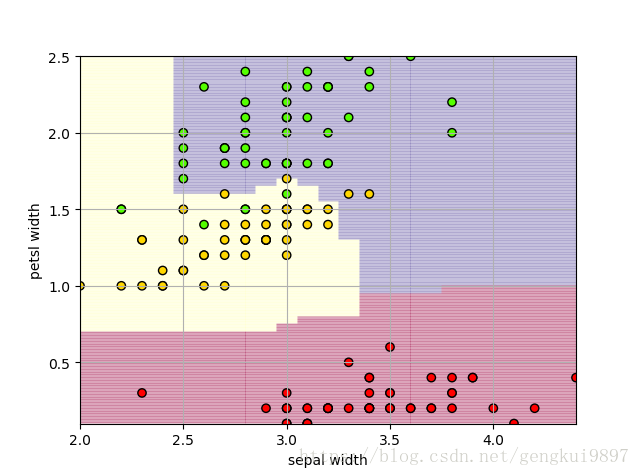
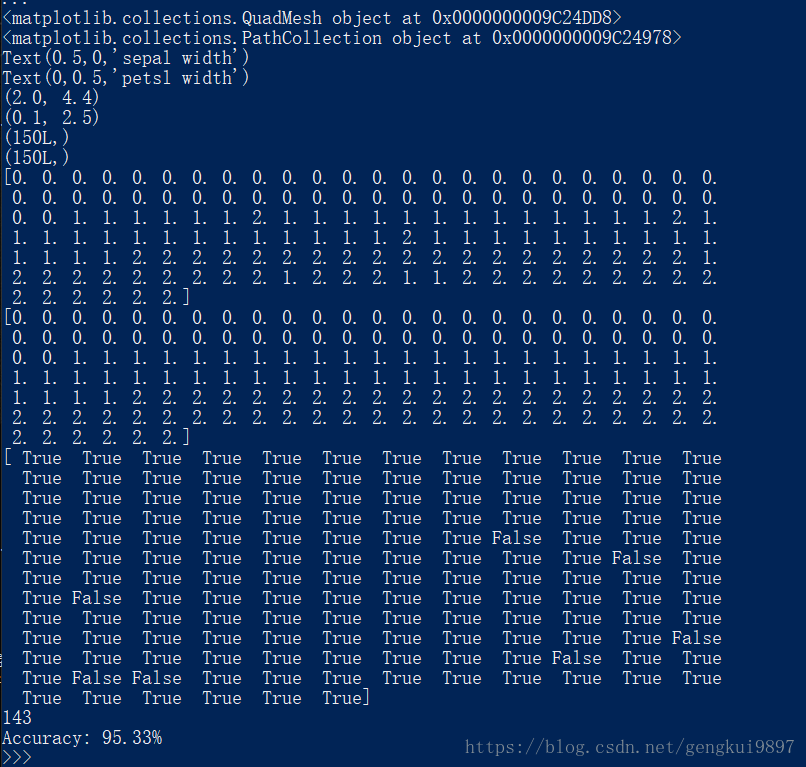
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(5)花瓣長度與花瓣寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,2:4]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#儲存
f = open("iris_tree.dot","w")
tree.export_graphviz(dt_clf,out_file=f)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[2])
plt.ylabel(iris_feature[3])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
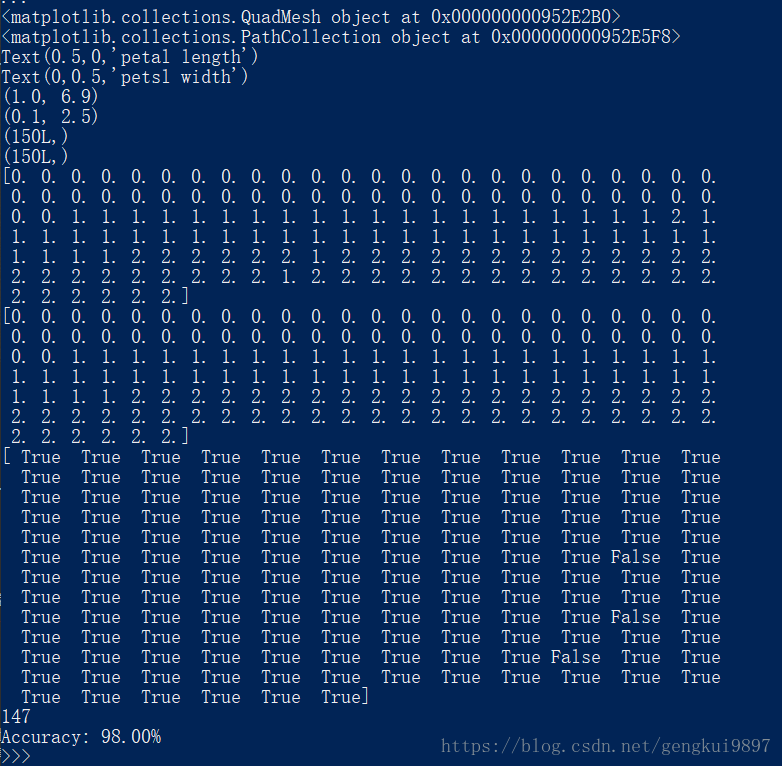
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))兩特徵隨機森林:
(1)花萼長度與花萼寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,:2]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = RandomForestClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[0])
plt.ylabel(iris_feature[1])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
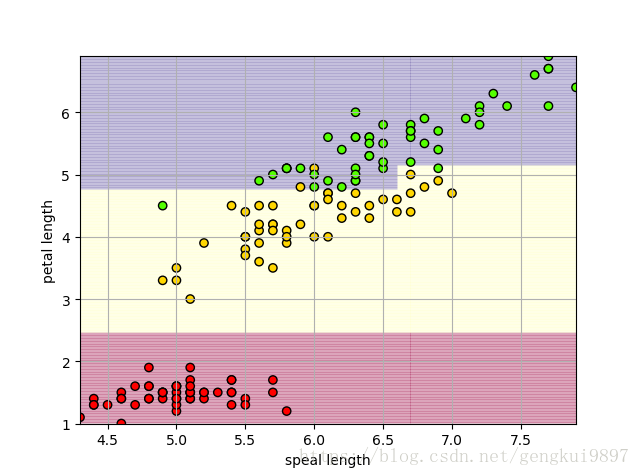
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(2)花萼長度與花瓣長度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,::2]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = RandomForestClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[0])
plt.ylabel(iris_feature[2])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
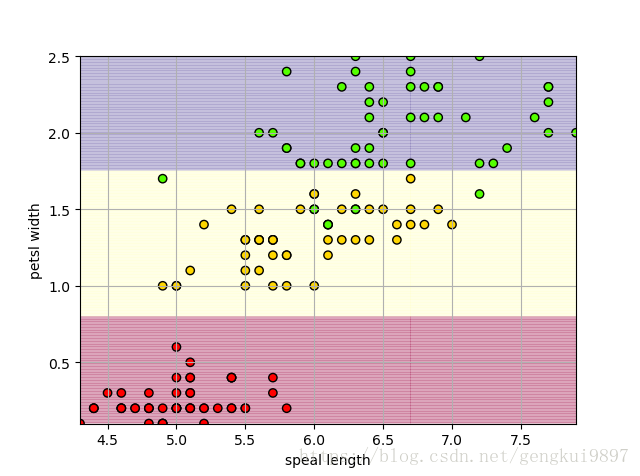
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(3)花萼長度與花瓣寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,::3]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = RandomForestClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[0])
plt.ylabel(iris_feature[3])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(4)花萼寬度與花瓣長度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,1:3]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = RandomForestClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[1])
plt.ylabel(iris_feature[2])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(5)花萼寬度與花瓣寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,1::2]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = RandomForestClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[1])
plt.ylabel(iris_feature[3])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(6)花瓣長度與花瓣寬度:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return it[s]
#花萼長度、花萼寬度、花瓣長度、花瓣寬度
iris_feature = 'speal length','sepal width','petal length','petsl width'
if __name__ == "__main__":
path = 'iris.data'#資料檔案路徑
#路徑,浮點型資料,逗號分隔,第4列用函式iris_type單獨處理
data = np.loadtxt(path,dtype=float,delimiter=',',converters={4:iris_type})
#將資料的0-3列組成x,第4列得到y
x,y = np.split(data,(4,),axis=1)
#為了視覺化,僅使用前兩列特徵
x = x[:,2:4]
#決策樹引數估計
#min_samples_split=10#如果該節點包含的樣本數目大於10,則(有可能)對其分支
#min_samples_leaf=10#若將某節點分支後,得到的每個子節點樣本數目都大於10,則完成分支,否則不完成分支
clf = RandomForestClassifier(criterion='entropy',min_samples_leaf=3)
dt_clf = clf.fit(x,y)
#畫圖
#橫縱各取樣多少個值
N,M = 500,500
#得到第0列範圍
x1_min,x1_max = x[:,0].min(),x[:,0].max()
#得到第1列範圍
x2_min,x2_max = x[:,1].min(),x[:,1].max()
t1 = np.linspace(x1_min,x1_max,N)
t2 = np.linspace(x2_min,x2_max,M)
#生成網格取樣點
x1,x2 = np.meshgrid(t1,t2)
#測試點
x_test = np.stack((x1.flat,x2.flat),axis=1)
#預測值
y_hat = dt_clf.predict(x_test)
#使之與輸入形狀相同
y_hat = y_hat.reshape(x1.shape)
#預測值的顯示
plt.pcolormesh(x1,x2,y_hat,cmap=plt.cm.Spectral,alpha=0.1)
plt.scatter(x[:,0],x[:,1],c=np.squeeze(y),edgecolors='k',cmap=plt.cm.prism)
#顯示樣本
plt.xlabel(iris_feature[2])
plt.ylabel(iris_feature[3])
plt.xlim(x1_min,x1_max)
plt.ylim(x2_min,x2_max)
plt.grid()
plt.show()
#訓練集上的預測結果
y_hat = dt_clf.predict(x)
y = y.reshape(-1)
print y_hat.shape
print y.shape
result = y_hat == y
print y_hat
print y
print result
c = np.count_nonzero(result)
print c
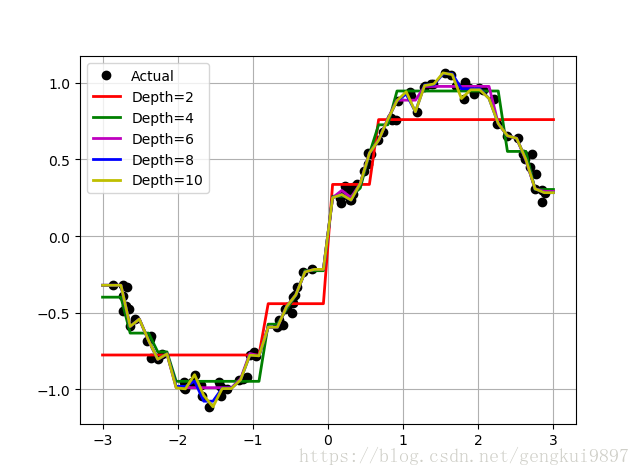
print 'Accuracy: %.2f%%' %(100*float(c)/float(len(result)))(二)使用sklearn的決策樹做迴歸
import numpy as np
from sklearn.tree import DecisionTreeRegressor as dtr
import matplotlib.pyplot as plt
N = 100
#[-3,3)
x = np.random.rand(N)*6-3
x.sort()
y = np.sin(x) + np.random.randn(N)*0.05
#轉置後,得到N個樣本,每個樣本都是一維的
x = x.reshape(-1,1)
#比較決策樹的深度
depth = [2,4,6,8,10]
clr = 'rgmby'
reg = [dtr(criterion='mse',max_depth=depth[0]),
dtr(criterion='mse',max_depth=depth[1]),
dtr(criterion='mse',max_depth=depth[2]),
dtr(criterion='mse',max_depth=depth[3]),
dtr(criterion='mse',max_depth=depth[4])]
plt.plot(x,y,'ko',linewidth=2,label='Actual')
x_test = np.linspace(-3,3,50).reshape(-1,1)
for i,r in enumerate(reg):
dt = r.fit(x,y)
y_hat = dt.predict(x_test)
plt.plot(x_test,y_hat,'-',color=clr[i],linewidth=2,label='Depth=%d' %depth[i])
plt.legend(loc='upper left')
plt.grid()
plt.show()
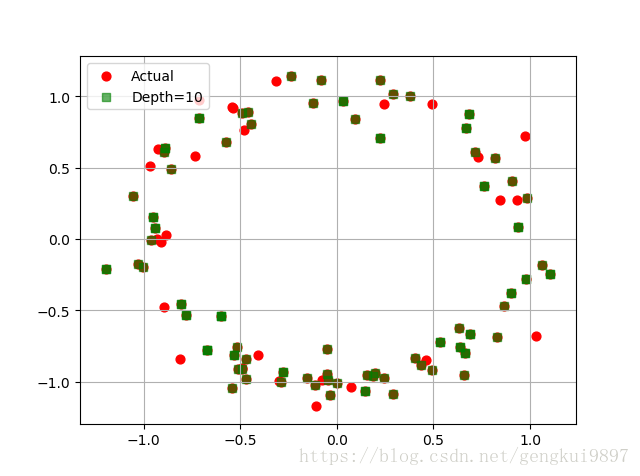
(三)決策樹多輸出預測
import numpy as np
from sklearn.tree import DecisionTreeRegressor as dtr
import matplotlib.pyplot as plt
N = 100
#[-4,4)
x = np.random.rand(N)*8-4
x.sort()
y1 = np.sin(x) + np.random.randn(N)*0.1
y2 = np.cos(x) + np.random.randn(N)*0.1
y = np.vstack((y1,y2)).T
#轉置後,得到N個樣本,每個樣本都是一維的
x = x.reshape(-1,1)
depth = 10
reg = dtr(criterion='mse',max_depth=depth)
dt = reg.fit(x,y)
x_test = np.linspace(-4,4,num=100).reshape(-1,1)
y_hat = dt.predict(x_test)
plt.scatter(y[:,0],y[:,1],c='r',s=40,label='Actual')
plt.scatter(y_hat[:,0],y_hat[:,1],c='g',marker='s',s=40,label='Depth=%d' %depth,alpha=0.6)
plt.legend(loc='upper left')
plt.grid()
plt.show()