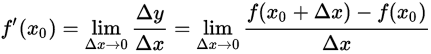tensorflow-梯度下降,有這一篇就足夠了
前言
最近機器學習越來越火了,前段時間斯丹福大學副教授吳恩達都親自錄製了關於Deep Learning Specialization的教程,在國內掀起了巨大的學習熱潮。本著不被時代拋棄的念頭,自己也開始研究有關機器學習的知識。都說機器學習的學習難度非常大,但不親自嘗試一下又怎麼會知道其中的奧妙與樂趣呢?只有不斷的嘗試才能找到最適合自己的道路。
請容忍我上述的自我煽情,下面進入主題。這篇文章主要對機器學習中所遇到的GradientDescent(梯度下降)進行全面分析,相信你看了這篇文章之後,對GradientDescent將徹底弄明白其中的原理。
梯度下降的概念
梯度下降法是一個一階最優化演算法,通常也稱為最速下降法。要使用梯度下降法找到一個函式的區域性極小值,必須向函式上當前點對於梯度(或者是近似梯度)的反方向的規定步長距離點進行迭代搜尋。所以梯度下降法可以幫助我們求解某個函式的極小值或者最小值。對於n維問題就最優解,梯度下降法是最常用的方法之一。下面通過梯度下降法的前生今世
梯度下降法的前世
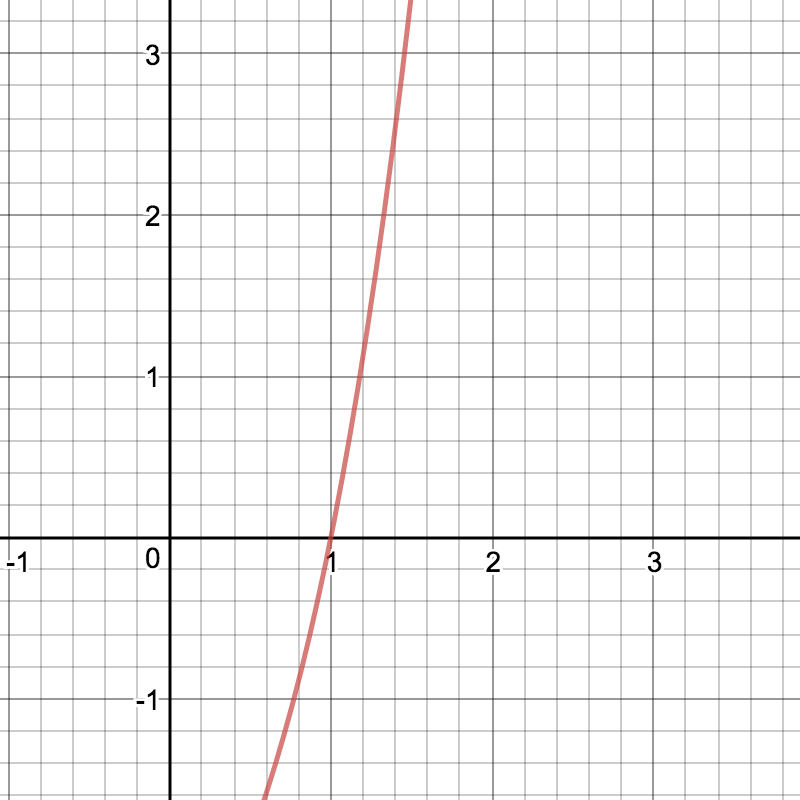
首先從簡單的開始,看下面的一維函式:
f(x) = x^3 + 2 * x - 3在數學中如果我們要求f(x) = 0處的解,我們可以通過如下誤差等式來求得:
error = (f(x) - 0)^2當error趨近於最小值時,也就是f(x) = 0處x的解,我們也可以通過圖來觀察:
通過這函式圖,我們可以非常直觀的發現,要想求得該函式的最小值,只要將x指定為函式圖的最低谷。這在高中我們就已經掌握了該函式的最小值解法。我們可以通過對該函式進行求導(即斜率):
derivative(x) = 6 * x^5 + 16 * x^3 - 18 * x^2 + 8 * x - 12 如果要得到最小值,只需令derivative(x) = 0,即x = 1。同時我們結合圖與導函式可以知道:
- 當
x < 1時,derivative < 0,斜率為負的; - 當
x > 1時,derivative > 0,斜率為正的; - 當
x 無限接近 1時,derivative也就無限=0,斜率為零。
通過上面的結論,我們可以使用如下表達式來代替x在函式中的移動
x = x - reate * derivative當斜率為負的時候,x增大,當斜率為正的時候,x減小;因此x總是會向著低谷移動,使得error最小,從而求得f(x) = 0處的解。其中的rate代表x逆著導數方向移動的距離,rate越大,x每次就移動的越多。反之移動的越少。
這是針對簡單的函式,我們可以非常直觀的求得它的導函式。為了應對複雜的函式,我們可以通過使用求導函式的定義來表達導函式:若函式f(x)在點x0處可導,那麼有如下定義:
上面是都是公式推導,下面通過程式碼來實現,下面的程式碼都是使用python進行實現。
>>> def f(x):
... return x**3 + 2 * x - 3
...
>>> def error(x):
... return (f(x) - 0)**2
...
>>> def gradient_descent(x):
... delta = 0.00000001
... derivative = (error(x + delta) - error(x)) / delta
... rate = 0.01
... return x - rate * derivative
...
>>> x = 0.8
>>> for i in range(50):
... x = gradient_descent(x)
... print('x = {:6f}, f(x) = {:6f}'.format(x, f(x)))
...執行上面程式,我們就能得到如下結果:
x = 0.869619, f(x) = -0.603123
x = 0.921110, f(x) = -0.376268
x = 0.955316, f(x) = -0.217521
x = 0.975927, f(x) = -0.118638
x = 0.987453, f(x) = -0.062266
x = 0.993586, f(x) = -0.031946
x = 0.996756, f(x) = -0.016187
x = 0.998369, f(x) = -0.008149
x = 0.999182, f(x) = -0.004088
x = 0.999590, f(x) = -0.002048
x = 0.999795, f(x) = -0.001025
x = 0.999897, f(x) = -0.000513
x = 0.999949, f(x) = -0.000256
x = 0.999974, f(x) = -0.000128
x = 0.999987, f(x) = -0.000064
x = 0.999994, f(x) = -0.000032
x = 0.999997, f(x) = -0.000016
x = 0.999998, f(x) = -0.000008
x = 0.999999, f(x) = -0.000004
x = 1.000000, f(x) = -0.000002
x = 1.000000, f(x) = -0.000001
x = 1.000000, f(x) = -0.000001
x = 1.000000, f(x) = -0.000000
x = 1.000000, f(x) = -0.000000
x = 1.000000, f(x) = -0.000000通過上面的結果,也驗證了我們最初的結論。x = 1時,f(x) = 0。
所以通過該方法,只要步數足夠多,就能得到非常精確的值。
梯度下降法的今生
上面是對一維函式進行求解,那麼對於多維函式又要如何求呢?我們接著看下面的函式,你會發現對於多維函式也是那麼的簡單。
f(x) = x[0] + 2 * x[1] + 4同樣的如果我們要求f(x) = 0處,x[0]與x[1]的值,也可以通過求error函式的最小值來間接求f(x)的解。跟一維函式唯一不同的是,要分別對x[0]與x[1]進行求導。在數學上叫做偏導數:
- 保持x[1]不變,對
x[0]進行求導,即f(x)對x[0]的偏導數 - 保持x[0]不變,對
x[1]進行求導,即f(x)對x[1]的偏導數
有了上面的理解基礎,我們定義的gradient_descent如下:
>>> def gradient_descent(x):
... delta = 0.00000001
... derivative_x0 = (error([x[0] + delta, x[1]]) - error([x[0], x[1]])) / delta
... derivative_x1 = (error([x[0], x[1] + delta]) - error([x[0], x[1]])) / delta
... rate = 0.01
... x[0] = x[0] - rate * derivative_x0
... x[1] = x[1] - rate * derivative_x1
... return [x[0], x[1]]
...rate的作用不變,唯一的區別就是分別獲取最新的x[0]與x[1]。下面是整個程式碼:
>>> def f(x):
... return x[0] + 2 * x[1] + 4
...
>>> def error(x):
... return (f(x) - 0)**2
...
>>> def gradient_descent(x):
... delta = 0.00000001
... derivative_x0 = (error([x[0] + delta, x[1]]) - error([x[0], x[1]])) / delta
... derivative_x1 = (error([x[0], x[1] + delta]) - error([x[0], x[1]])) / delta
... rate = 0.02
... x[0] = x[0] - rate * derivative_x0
... x[1] = x[1] - rate * derivative_x1
... return [x[0], x[1]]
...
>>> x = [-0.5, -1.0]
>>> for i in range(100):
... x = gradient_descent(x)
... print('x = {:6f},{:6f}, f(x) = {:6f}'.format(x[0],x[1],f(x)))
...輸出結果為:
x = -0.560000,-1.120000, f(x) = 1.200000
x = -0.608000,-1.216000, f(x) = 0.960000
x = -0.646400,-1.292800, f(x) = 0.768000
x = -0.677120,-1.354240, f(x) = 0.614400
x = -0.701696,-1.403392, f(x) = 0.491520
x = -0.721357,-1.442714, f(x) = 0.393216
x = -0.737085,-1.474171, f(x) = 0.314573
x = -0.749668,-1.499337, f(x) = 0.251658
x = -0.759735,-1.519469, f(x) = 0.201327
x = -0.767788,-1.535575, f(x) = 0.161061
x = -0.774230,-1.548460, f(x) = 0.128849
x = -0.779384,-1.558768, f(x) = 0.103079
x = -0.783507,-1.567015, f(x) = 0.082463
x = -0.786806,-1.573612, f(x) = 0.065971
x = -0.789445,-1.578889, f(x) = 0.052777
x = -0.791556,-1.583112, f(x) = 0.042221
x = -0.793245,-1.586489, f(x) = 0.033777
x = -0.794596,-1.589191, f(x) = 0.027022
x = -0.795677,-1.591353, f(x) = 0.021617
x = -0.796541,-1.593082, f(x) = 0.017294
x = -0.797233,-1.594466, f(x) = 0.013835
x = -0.797786,-1.595573, f(x) = 0.011068
x = -0.798229,-1.596458, f(x) = 0.008854
x = -0.798583,-1.597167, f(x) = 0.007084
x = -0.798867,-1.597733, f(x) = 0.005667
x = -0.799093,-1.598187, f(x) = 0.004533
x = -0.799275,-1.598549, f(x) = 0.003627
x = -0.799420,-1.598839, f(x) = 0.002901
x = -0.799536,-1.599072, f(x) = 0.002321
x = -0.799629,-1.599257, f(x) = 0.001857
x = -0.799703,-1.599406, f(x) = 0.001486
x = -0.799762,-1.599525, f(x) = 0.001188
x = -0.799810,-1.599620, f(x) = 0.000951
x = -0.799848,-1.599696, f(x) = 0.000761
x = -0.799878,-1.599757, f(x) = 0.000608
x = -0.799903,-1.599805, f(x) = 0.000487
x = -0.799922,-1.599844, f(x) = 0.000389
x = -0.799938,-1.599875, f(x) = 0.000312
x = -0.799950,-1.599900, f(x) = 0.000249
x = -0.799960,-1.599920, f(x) = 0.000199
x = -0.799968,-1.599936, f(x) = 0.000159
x = -0.799974,-1.599949, f(x) = 0.000128
x = -0.799980,-1.599959, f(x) = 0.000102
x = -0.799984,-1.599967, f(x) = 0.000082
x = -0.799987,-1.599974, f(x) = 0.000065
x = -0.799990,-1.599979, f(x) = 0.000052
x = -0.799992,-1.599983, f(x) = 0.000042
x = -0.799993,-1.599987, f(x) = 0.000033
x = -0.799995,-1.599989, f(x) = 0.000027
x = -0.799996,-1.599991, f(x) = 0.000021
x = -0.799997,-1.599993, f(x) = 0.000017
x = -0.799997,-1.599995, f(x) = 0.000014
x = -0.799998,-1.599996, f(x) = 0.000011
x = -0.799998,-1.599997, f(x) = 0.000009
x = -0.799999,-1.599997, f(x) = 0.000007
x = -0.799999,-1.599998, f(x) = 0.000006
x = -0.799999,-1.599998, f(x) = 0.000004
x = -0.799999,-1.599999, f(x) = 0.000004
x = -0.799999,-1.599999, f(x) = 0.000003
x = -0.800000,-1.599999, f(x) = 0.000002
x = -0.800000,-1.599999, f(x) = 0.000002
x = -0.800000,-1.599999, f(x) = 0.000001
x = -0.800000,-1.600000, f(x) = 0.000001
x = -0.800000,-1.600000, f(x) = 0.000001
x = -0.800000,-1.600000, f(x) = 0.000001
x = -0.800000,-1.600000, f(x) = 0.000001
x = -0.800000,-1.600000, f(x) = 0.000000細心的你可能會發現,f(x) = 0不止這一個解還可以是x = -2, -1。這是因為梯度下降法只是對當前所處的凹谷進行梯度下降求解,對於error函式並不代表只有一個f(x) = 0的凹谷。所以梯度下降法只能求得區域性解,但不一定能求得全部的解。當然如果對於非常複雜的函式,能夠求得區域性解也是非常不錯的。
tensorflow中的運用
通過上面的示例,相信對梯度下降也有了一個基本的認識。現在我們回到最開始的地方,在tensorflow中使用gradientDescent。
import tensorflow as tf
# Model parameters
W = tf.Variable([.3], dtype=tf.float32)
b = tf.Variable([-.3], dtype=tf.float32)
# Model input and output
x = tf.placeholder(tf.float32)
linear_model = W*x + b
y = tf.placeholder(tf.float32)
# loss
loss = tf.reduce_sum(tf.square(linear_model - y)) # sum of the squares
# optimizer
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# training data
x_train = [1, 2, 3, 4]
y_train = [0, -1, -2, -3]
# training loop
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init) # reset values to wrong
for i in range(1000):
sess.run(train, {x: x_train, y: y_train})
# evaluate training accuracy
curr_W, curr_b, curr_loss = sess.run([W, b, loss], {x: x_train, y: y_train})
print("W: %s b: %s loss: %s"%(curr_W, curr_b, curr_loss))上面的是tensorflow的官網示例,上面程式碼定義了函式linear_model = W * x + b,其中的error函式為linear_model - y。目的是對一組x_train與y_train進行簡單的訓練求解W與b。為了求得這一組資料的最優解,將每一組的error相加從而得到loss,最後再對loss進行梯度下降求解最優值。
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)在這裡rate為0.01,因為這個示例也是多維函式,所以也要用到偏導數來進行逐步向最優解靠近。
for i in range(1000):
sess.run(