資料結構之二叉排序樹(C語言實現)
一、基本概念
1.二叉排序樹
二叉排序樹(Binary sort tree,BST),又稱為二叉查詢樹,或者是一棵空樹;或者是具有下列性質的二叉樹:
(1)若它的左子樹不為空,則左子樹上所有節點的值均小於它的根節點的值;
(2)若它的右子樹不為空,則右子樹上所有節點的值均大於它的根節點的值;
(3)它的左、右子樹也分別為二叉排序樹。
二、二叉排序樹操作
二叉排序樹是一種動態樹表。它的特點是樹的結構不是一次生成的,而是在查詢過程中,當樹中不存在關鍵字等於給定值的節點時再進行插入。新插入的節點一定是一個新新增的葉子結點,並且是查詢不成功時查詢路徑上訪問的最後一個節點的左孩子或右孩子節點,
二叉排序樹的操作有插入、刪除、查詢和遍歷等。
注意:二叉排序樹中沒有值相同的節點
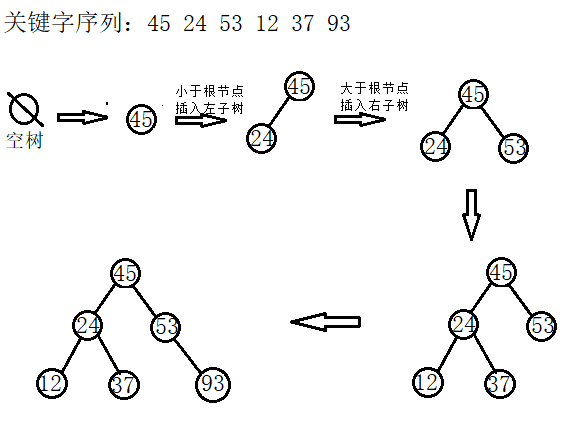
(1)插入
a.插入過程比較簡單,首先判斷當前要插入的值是否已經存在二叉排序樹中,如果已經存在,則直接返回;如果不存在,則轉b;
b.當前要插入的值不存在,則應找到適當的位置,將其插入。注意插入的新節點一定是葉子節點;
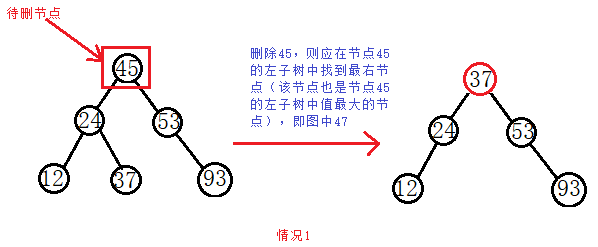
(2)刪除
a.和插入一樣,要刪除一個給定值的節點,首先要判斷這樣節點是否存在,如果已經不存在,則直接返回;如果已經存在,則獲取給定值節點的位置,根據不同情況進行刪除、調整,轉b;
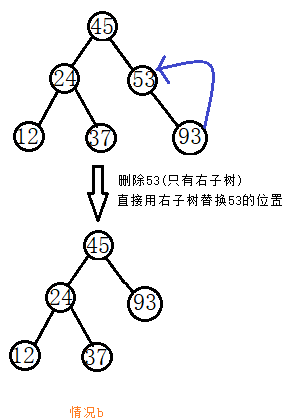
b.如果待刪節點只有左子樹(只有右子樹),則直接將待刪節點的左子樹(右子樹)放在待刪節點的位置,並釋放待刪節點的記憶體,否則轉c;
c.如果待刪節點既有左子樹又有右子樹,此時的刪除可能有點複雜,但是也比較好理解。就是在待刪節點的左子樹中找到值最大的那個節點,將其放到待刪節點的位置。
(3)查詢
查詢過程比較簡單,首先將關鍵字和根節點的關鍵字比較,如果相等則返回節點的位置(指標);否則,如果小於根節點的關鍵字,則去左子樹中繼續查詢;如果大於根節點的關鍵字,則去右子樹中查詢;如果找到葉子節點也沒找到,則返回NULL。
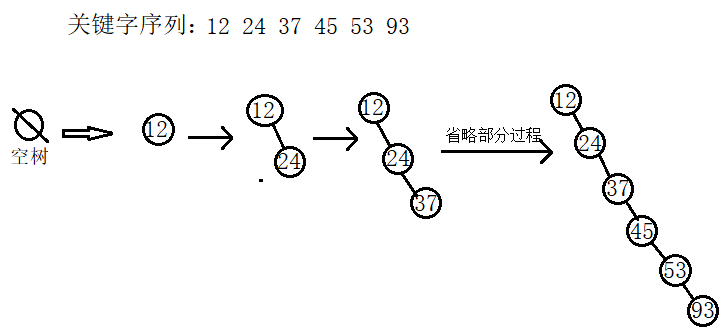
查詢過程的最好情況就是上面的圖中那樣,節點在左右子樹中分佈比較均勻,此時查詢的時間複雜度為O(logn);最壞的情況就是在建立二叉排序樹時,輸入的關鍵字序列正好是有序的,此時形成的二叉排序樹是一棵單支二叉樹,此時查詢退化成了單鏈表的查詢,時間的複雜度為O(n).如下圖:
(4)遍歷
由上面二排序樹的定義可知,左子樹的所有值均小於根節點,右子樹的所有值均大於根節點,而這個特點正好和二叉樹的中序遍歷中--左子樹->根節點->右子樹不謀而合,所以對二叉排序樹進行中序遍歷得到的正好是一個有序的
三、原始碼實現(C語言程式碼)
#include <stdio.h>
#include <stdlib.h>
//二叉排序樹
typedef struct BSTNode
{
int data;
BSTNode *lchild; //左孩子
BSTNode *rchild; //右孩子
}BSTNode,*BSTree;
bool Search(BSTree bst, int key, BSTree f, BSTree *p);
void InOderTraverse(BSTree bst) //中序遞迴遍歷二叉樹
{
if (NULL != bst)
{
InOderTraverse(bst->lchild);
printf("%d ", bst->data);
InOderTraverse(bst->rchild);
}
}
static BSTNode* BuyNode(int data) //生成一個節點並進行初始化
{
BSTNode *pTmp = (BSTNode*)malloc(sizeof(BSTNode));
if (NULL == pTmp)
{
exit(0);
}
pTmp->data = data;
pTmp->lchild = NULL;
pTmp->rchild = NULL;
return pTmp;
}
bool Insert(BSTree *bst, int key)
{
if (NULL == *bst) //空樹
{
*bst = BuyNode(key); //插入根節點
return true;
}
BSTNode *p;
//先在二叉排序樹中查詢要插入的值是否已經存在
if (!Search(*bst, key, NULL, &p)) //如果查詢失敗,則插入;此時p指向遍歷的最後一個節點
{
BSTNode *pNew = BuyNode(key);
if (key < p->data) //將s作為p的左孩子
{
p->lchild = pNew;
}
else if (key > p->data) //將s作為p的右孩子
{
p->rchild = pNew;
}
return true; //插入成功
}
else
{
printf("\nThe node(%d) already exists.\n", key);
}
return false;
}
/*
刪除分三種情況:
(1)被刪除的節點無孩子,說明該節點是葉子節點,直接刪
(2)被刪除的節點只有左孩子或者右孩子,直接刪,並將其左孩子或者右孩子放在被刪節點的位置
(3)被刪除的節點既有右孩子又有右孩子
*/
void Delete(BSTree bst, int key)
{
if (NULL == bst)
{
exit(1); //空樹直接報錯
}
BSTNode *p;
BSTNode *f = NULL;
BSTNode *q, *s;
if (Search(bst, key, NULL, &p)) //確實存在值為key的節點,則p指向該節點
{
if (NULL == p->lchild && NULL != p->rchild) //無左孩子,有右孩子
{
q = p->rchild; //注意這裡我刪除節點的方式,類似於在單鏈表中在不知道前驅節點的情況下刪除當前節點
p->data = q->data; //因為兩個節點之間本質的不同在於資料域的不同,而與放在哪個地址沒有關係
p->rchild = q->rchild;
p->lchild = q->lchild;
free(q);
}
else if (NULL == p->rchild && NULL != p->lchild) //無右孩子,有左孩子
{
q = p->lchild;
p->data = q->data;
p->rchild = q->rchild;
p->lchild = q->lchild;
free(q);
}
else //既有左孩子,又有右孩子
{
q = p;
s = p->lchild; //找左孩子的最右孩子
while (s->rchild)
{
q = s;
s = s->rchild;
}
p->data = s->data;
if (q != p)
{
q->rchild = p->lchild;
}
else
{
q->lchild = s->lchild;
}
free(s);
}
}
}
bool Search(BSTree bst, int key, BSTree f, BSTree *p) //查詢成功時,p指向值為key的節點。如果查詢失敗,則p指向遍歷的最後一個節點
{
if (!bst)
{
*p = f;
return false;
}
if (bst->data == key) //查詢成功,直接返回
{
*p = bst;
return true;
}
else if (bst->data < key)
{
return Search(bst->rchild, key, bst, p);
}
return Search(bst->lchild, key, bst, p);
}
int main(void)
{
BSTNode *root = NULL;
Insert(&root, 45);
Insert(&root, 24);
Insert(&root, 53);
Insert(&root, 12);
Insert(&root, 90);
InOderTraverse(root);
printf("\n%d ", Insert(&root, 45)); //輸出0表示插入失敗,輸出1表示插入成功
printf("%d\n", Insert(&root, 4));
InOderTraverse(root);
printf("\n");
Delete(root, 45); //刪除節點45
InOderTraverse(root);
return 0;
}
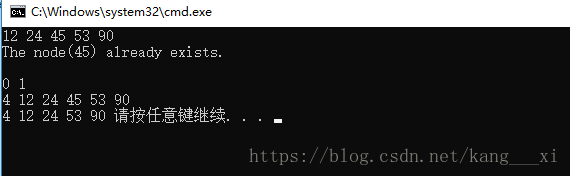
執行結果: