功能

插入：insert()
查詢：search()
刪除：remove()
清除整個樹：clear()
最大值：max()
最小值：min()
前序遍歷：PreOrder()
中序遍歷：InOrder()
後序遍歷：PostOrder()
注：此二叉樹允許插入相同的值，且預設將其放在右子樹，因此以後會考慮寫unique()函式

模板類的宣告

template<typename T>
struct BSnode      //二叉樹的結點
{
	T         data;   //資料
	BSnode<T> *lChild;//左孩子
	BSnode<T> *rChild;//右孩子
	BSnode<T> *parent;//雙親,方便刪除操作
	BSnode(const T& Data, BSnode<T> *left, BSnode<T> *right, BSnode<T> *par):
		data(Data),lChild(left),rChild(right),parent(par){}
};


template<typename T>
class BStree {
	BSnode<T>  *root;
public:
	/*構造與解構函式*/
	BStree() :root(nullptr) {}
	BStree(int rootValue) { root = nullptr; insert(rootValue); }
	//BStree(const BStree<T>& that);
	~BStree();

	/*其他操作*/
	void insert(const T& data);                //插入一個數據
	BSnode<T>* search(const T& data) const;    //查詢第一個相等的值的地址
	void remove(const T& data);		         //根據值刪除結點
	void clear();                              //清除整個樹
	BSnode<T>* max();						//找到最大值
	BSnode<T>* min();						//找到最小值

	/*遍歷*/
	void PreOrder() const;
	void InOrder() const;
	void PostOrder() const;
	
private:
	void insert(BSnode<T>* pFindNode, BSnode<T>* pInsertNode);
	BSnode<T>* search(BSnode<T>* proot, const T& data) const;     //搜尋
	void remove(BSnode<T>* pFind, BSnode<T>* pParent);		      //pFind為待刪除的結點，pParent其雙親結點
	void clear(BSnode<T>*& proot);							  //注意，這裡的引數一定要傳引用或者二級指標。
	BSnode<T>* max(BSnode<T>* proot);							  //設定從proot開始找					 
	BSnode<T>* min(BSnode<T>* proot);							  //設定從proot開始找	  

	void PreOrder(BSnode<T> *proot) const;
	void InOrder(BSnode<T> *proot) const;
	void PostOrder(BSnode<T> *proot) const;

};
 

具體實現

template<typename T>
inline BStree<T>::~BStree()
{
	clear();
}

template<typename T>
inline void BStree<T>::insert(const T & data)
{
	BSnode<T> *pNode = new BSnode<T>(data, nullptr, nullptr,nullptr);
	if (root == nullptr)
		root = pNode;
	else
	{
		insert(root, pNode);
	}
}

template<typename T>
inline BSnode<T>* BStree<T>::search(const T & data) const
{
	return search(root,data);
}

template<typename T>
inline void BStree<T>::remove(const T & data)
{
	BSnode<T>* findNode = const_cast<BSnode<T>*>(search(data));
	if (findNode == nullptr)
		return;
	else
	{
		BSnode<T>* pTemp = findNode->rChild;
		remove(findNode, findNode->parent);
		while (pTemp != nullptr && pTemp->data == data)//如果仍然有相同的值，繼續刪除
		{
			remove(pTemp,pTemp->parent);
		}
	}
}

template<typename T>
inline void BStree<T>::PreOrder() const
{
	PreOrder(root);
}

template<typename T>
inline void BStree<T>::InOrder() const
{
	InOrder(root);
}

template<typename T>
inline void BStree<T>::PostOrder() const
{
	PostOrder(root);
}

template<typename T>
inline void BStree<T>::clear()
{
	clear(root);
}

template<typename T>
inline BSnode<T>* BStree<T>::max()
{
	return max(root);
}

template<typename T>
inline BSnode<T>* BStree<T>::min()
{
	return min(root);
}

template<typename T>
inline void BStree<T>::insert(BSnode<T>* pFindNode, BSnode<T>* pInsertNode)
{
	if (pFindNode->data > pInsertNode->data)
	{
		if (pFindNode->lChild == nullptr)
		{
			pFindNode->lChild = pInsertNode;
			pInsertNode->parent = pFindNode;
		}
		else
			insert(pFindNode->lChild, pInsertNode);
	}
	else
	{
		if (pFindNode->rChild == nullptr)
		{
			pFindNode->rChild = pInsertNode;
			pInsertNode->parent = pFindNode;
		}
		else
			insert(pFindNode->rChild, pInsertNode);
	}
}

template<typename T>
inline BSnode<T>* BStree<T>::search(BSnode<T>* proot, const T & data) const
{
	if (proot == nullptr)
		return nullptr;           //沒找到返回空
	if (proot->data == data)
		return proot;
	else if (proot->data > data)
		return search(proot->lChild, data);
	else
		return search(proot->rChild, data);
}

template<typename T>
inline void BStree<T>::remove(BSnode<T>* pFind, BSnode<T>* pParent)
{
	if (pParent == nullptr) //不能刪除根節點
		return;
	if (pFind->data < pParent->data)//如果要刪除的值在左半部分
	{
		if (pFind->lChild == nullptr && pFind->rChild == nullptr) //如果是葉子結點
			pParent->lChild = nullptr;
		else if (pFind->rChild == nullptr)//如果右子樹為空
		{
			pParent->lChild = pFind->lChild;
			pFind->lChild->parent = pParent;
		}
		else if (pFind->lChild == nullptr)//如果左子樹為空
		{
			pParent->lChild = pFind->rChild;
			pFind->rChild->parent = pParent;
		}
		else//如果都不為空
		{
			BSnode<T>* par = pFind;
			BSnode<T>* s = pFind->rChild;
			while (s->lChild != nullptr)
			{
				par = s;
				s = s->lChild;
			}
			pFind->data = s->data;
			if (par == pFind)   //如果pFind的右孩子就是大於pFind值的最小值結點
				par->rChild = s->rChild;
			else
				par->lChild = s->rChild;

			if(s->rChild)
			s->rChild->parent = par;
			delete s;
			return;
		}
	}
	else               //如果要刪除的值在右半部分
	{
		if (pFind->lChild == nullptr && pFind->rChild == nullptr) //如果是葉子結點
			pParent->rChild = nullptr;
		else if (pFind->rChild == nullptr)//如果右子樹為空
		{
			pParent->rChild = pFind->lChild;
			pFind->lChild->parent = pParent;
		}
		else if (pFind->lChild == nullptr)//如果左子樹為空
		{
			pParent->rChild = pFind->rChild;
			pFind->rChild->parent = pParent;
		}
		else//如果都不為空
		{
			BSnode<T>* par = pFind;
			BSnode<T>* s = pFind->lChild;
			while (s->rChild != nullptr)
			{
				par = s;
				s = s->rChild;
			}
			pFind->data = s->data;
			if (par == pFind)   //如果pFind的右孩子就是小於pFind值的最大值結點
				par->lChild = s->lChild;
			else
				par->rChild = s->lChild;

			if(s->lChild)
				s->lChild->parent = par;
			delete s;
			return;
		}
	}
	delete pFind;
}

template<typename T>
inline void BStree<T>::PreOrder(BSnode<T>* proot) const
{
	if (proot != nullptr)
	{
		cout << proot->data<<" ";
		PreOrder(proot->lChild);
		PreOrder(proot->rChild);
	}
}

template<typename T>
inline void BStree<T>::InOrder(BSnode<T>* proot)const
{
	if (proot != nullptr)
	{
		InOrder(proot->lChild);
		cout << proot->data << " ";
		InOrder(proot->rChild);
	}
}

template<typename T>
inline void BStree<T>::PostOrder(BSnode<T>* proot)const
{
	if (proot != nullptr)
	{
		PostOrder(proot->lChild);
		PostOrder(proot->rChild);
		cout << proot->data << " ";
	}
}

template<typename T>
inline void BStree<T>::clear(BSnode<T>*& proot)
{
	if (proot != nullptr)
	{
		clear(proot->lChild);     //遞迴刪除左子樹
		clear(proot->rChild);	  //遞迴刪除右子樹
		delete proot;
		proot = nullptr;
	}
}

template<typename T>
inline BSnode<T>* BStree<T>::max(BSnode<T>* proot)
{
	while (proot->rChild != nullptr)
		proot = proot->rChild;
	return proot;
}

template<typename T>
inline BSnode<T>* BStree<T>::min(BSnode<T>* proot)
{
	while (proot->lChild != nullptr)
		proot = proot->lChild;
	return proot;
}
 

測試程式碼

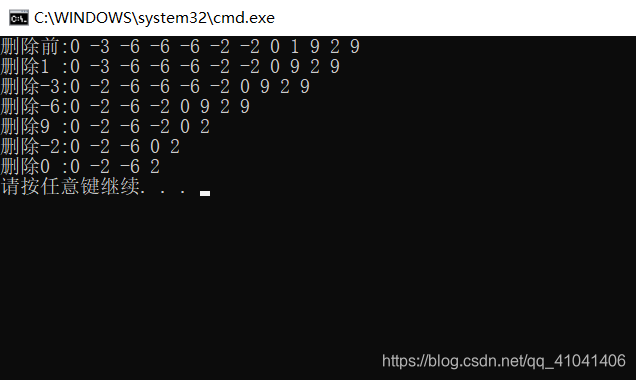
 #include<iostream>
#include"BStree.h"
using namespace std;

int main()
{
	using BSI = BStree<int>;
	BSI test(0);
	int arr[] = {0,-3,-6,-6,-6,-2,-2,1,9,2,9 };
	int n = sizeof(arr) / sizeof(int);
	for (int i = 0; i < n; ++i)
	{
		test.insert(arr[i]);
	}
	cout << "刪除前:";
	test.PreOrder(); cout << endl; 
	BSnode<int>* find = test.search(1);
	test.remove(find->data);
	cout << "刪除1 :"; test.PreOrder(); cout << endl;
	test.remove(-3); 
	cout << "刪除-3:"; test.PreOrder(); cout << endl;
	test.remove(-6);
	cout << "刪除-6:"; test.PreOrder(); cout << endl;
	test.remove(9);
	cout << "刪除9 :"; test.PreOrder(); cout << endl;
	test.remove(-2);
	cout << "刪除-2:"; test.PreOrder(); cout << endl;
	test.remove(0);
	cout << "刪除0 :"; test.PreOrder(); cout << endl;
}
 

測試結果