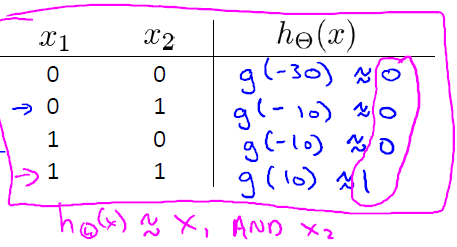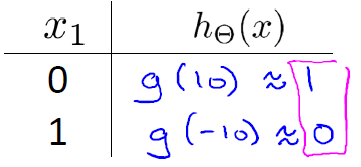【機器學習】神經網路(一)——多類分類問題
一、問題引入
早在監督學習中我們已經使用Logistic迴歸很好地解決二類分類問題。但現實生活中,更多的是多類分類問題(比如識別10個手寫數字)。本文引入神經網路模型解決多類分類問題。
二、神經網路模型介紹
神經網路模型是一個非常強大的模型,起源於嘗試讓機器模仿大腦的演算法,在80年代和90年代早期非常流行。同時它又是一個十分複雜的模型,導致其計算量非常巨大,所以在90年代後期逐漸衰落。近年來得益於計算機硬體能力,又開始流行起來。人類的大腦是一個十分神奇的東西,儘管當今人工智慧科技已經十分發達,但很大程度上,無論建立一個多麼完美的模型,其學習能力目前仍然遜色於大腦。因此神經網路是人工智慧領域的一個熱門研究方向。
1.神經網路模型
為了描述神經網路模型,我們先從最簡單的神經網路講起,這個神經網路僅由一個“神經元”構成,以下即是這個“神經元”的圖示:
其中x1, x2, x3稱為輸入(來自與其他神經元的輸入訊號), x0稱為偏置單元(bias unit), θ稱為權重或引數, hθ(x)稱為啟用函式(activation function), 這裡的啟用函式用了sigmoid(logistic) 函式:
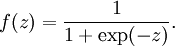
多個神經元組合在一起,便形成了神經網路,如下圖:
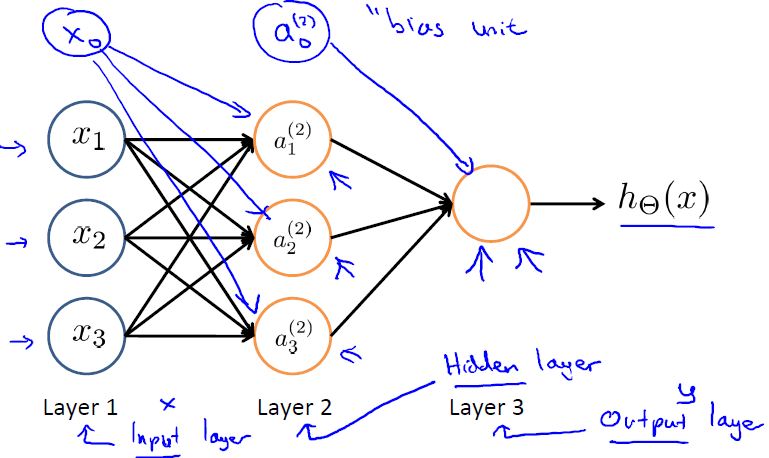
第一層稱為輸入層(input layer),第二層是隱藏層(hidden layer),第三層是輸出層(output layer),注意輸入層和隱藏層都存在一個偏置單元(bias unit)。其中,x0 是第一層的偏置單元(設定為1),
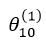 是對應該偏置單元 x0 的權值;
是對應該偏置單元 x0 的權值;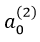 是第二層的偏置單元,
是第二層的偏置單元,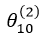
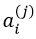 是第j層的第i個啟用函式,
是第j層的第i個啟用函式,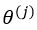 從第j層對映到第j+1層的控制函式的權重矩陣。計算啟用值時(以
從第j層對映到第j+1層的控制函式的權重矩陣。計算啟用值時(以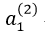 為例)按照下式計算:
為例)按照下式計算: 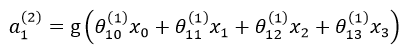
以此類推,上述神經網路模型可表示為:
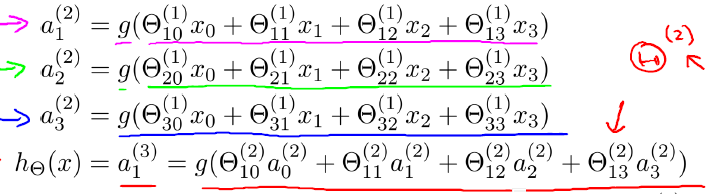
從該計算過程可以看出,神經網路在對樣本進行預測時,是從第一層(輸入層)開始,層層向前計算啟用值,直觀上看這是一種層層向前傳播特徵或者說層層向前啟用的過程,最終計算出
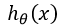 ,這個過程稱之為前向傳播(forward propagation)。
,這個過程稱之為前向傳播(forward propagation)。 其實,啟用函式的作用可以看作是從原始特徵學習出新特徵,或者說是將原始特徵從低維空間對映到高維空間。一開始也許無法很好的理解啟用函式的意義和作用,但一定要記住,引入啟用函式是神經網路具有優異效能的關鍵所在,多層級聯的結構加上啟用函式,令多層神經網路可以逼近任意函式,從而可以學習出非常複雜的假設函式。
2.學習布林代數
(1)學習AND
AND運算應該非常熟悉了,表示式如下:
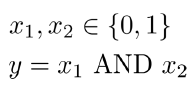
真值表如下:
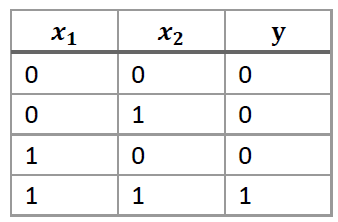
我們可以用以下模型學習AND函式:
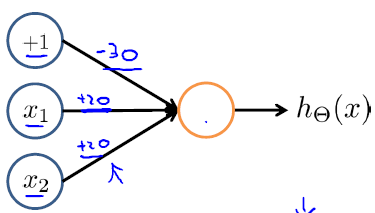
輸出函式可用下式表示:
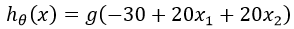
當我們依次按照真值表把輸入值代入此式,並根據sigmoid函式的性質,得到:
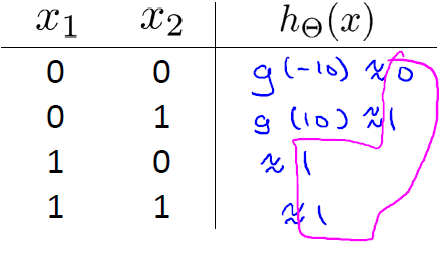
(2)學習OR函式
同樣地,學習OR函式的模型如下:
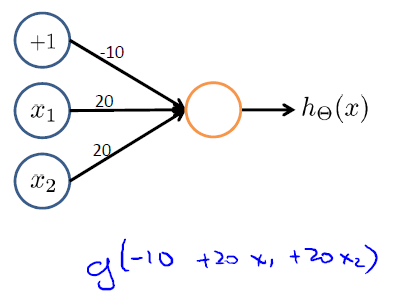
根據真值表輸入這個模型,得到:
(3)學習NOT函式
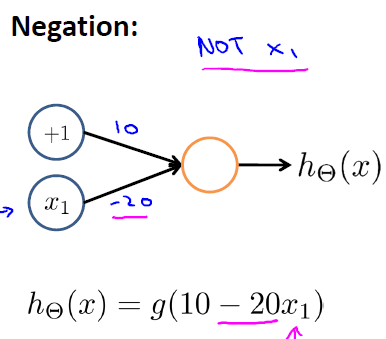
(4)學習XOR(異或)函式
學習XOR函式就不能使用單層神經網路實現了。因為XOR函式不是線性可分的(如圖所示,無法畫一條直線把0和1輸出值分開)
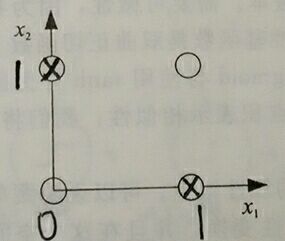
單層神經網路只能近似學習線性函式,而XOR函式需要先轉化AND、OR、NOT函式組合再建立多層神經網路模型。
3.多類分類問題
對於一張輸入圖片,需要識別其屬於行人、轎車、摩托車或者卡車中的一個型別,就是一個多類分類的問題。用神經網路表示如下:
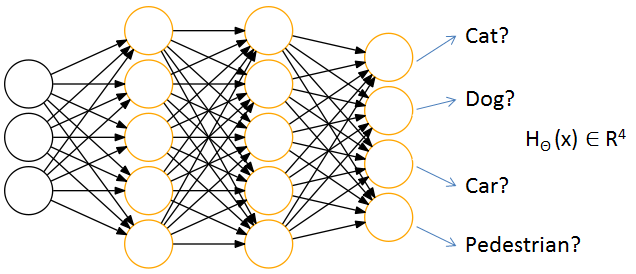
可以說,神經網路就是由一個個邏輯迴歸模型連線而成的,它們彼此作為輸入和輸出。最終輸出結果可表示為:
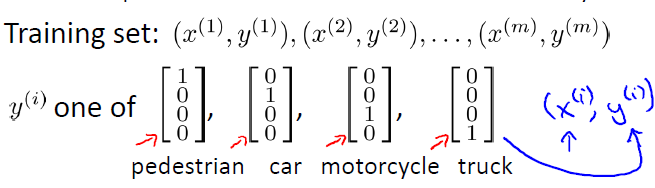
這與之前邏輯迴歸中的多類分類表示不同,在邏輯迴歸中,輸出y屬於類似於{1, 2, 3, 4}中的某個值,而這裡輸出的是一個向量。因此,神經網路解決多類分類問題的本質是把原分類問題分解為一類對其他類(one-vs-all)的二類分類問題。
神經網路比直接使用Logistic迴歸的優勢在於:如果給定基礎特徵的數量為100,那麼在利用Logistic迴歸解決複雜分類問題時會遇到特徵項爆炸增長,造成過擬合以及運算量過大問題。而對於神經網路,可以通過隱藏層數量和隱藏單元數量來控制假設函式的複雜程度,並且在計算時只計算一次項特徵變數。其實本質上來說,神經網路是通過這樣一個網路結構隱含地找到了所需要的高次特徵項,從而化簡了繁重的計算。
三、程式碼實現
1.計算啟用值
function p = predict(Theta1, Theta2, X)
m = size(X, 1);
num_labels = size(Theta2, 1);
a1 = [ones(m,1), X];
a2 = sigmoid(a1 * Theta1');
a2 = [ones(m,1), a2];
a3 = sigmoid(a2 * Theta2');
[~, p] = max(a3, [], 2);
end這裡我們構建的神經網路有單個隱藏層。
2.匯入資料並識別
(1)先匯入影象資料
%% =========== Part 1: Loading and Visualizing Data =============
% We start the exercise by first loading and visualizing the dataset.
% You will be working with a dataset that contains handwritten digits.
%
% Load Training Data
fprintf('Loading and Visualizing Data ...\n')
load('ex3data1.mat');
m = size(X, 1);
% Randomly select 100 data points to display
sel = randperm(size(X, 1));
sel = sel(1:100);
displayData(X(sel, :));
fprintf('Part 1 Program paused. Press enter to continue.\n');
pause;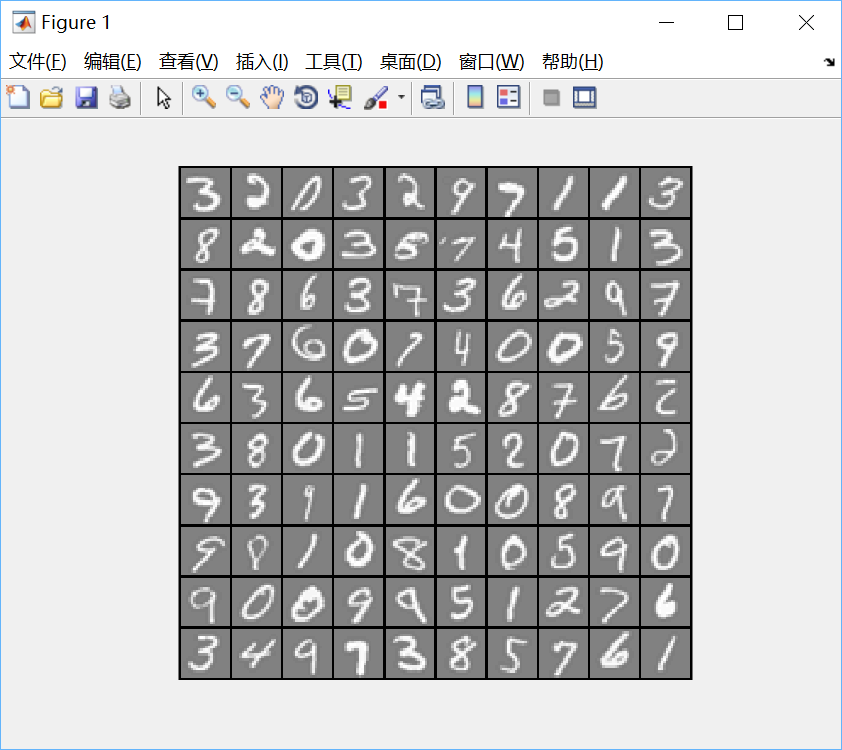
圖中都是一些手寫的數字。
(2)匯入模型引數
%% ================ Part 2: Loading Pameters ================
% In this part of the exercise, we load some pre-initialized
% neural network parameters.
fprintf('\nLoading Saved Neural Network Parameters ...\n')
% Load the weights into variables Theta1 and Theta2
load('ex3weights.mat');(3)對手寫數字進行識別
%% ================= Part 3: Implement Predict =================
% After training the neural network, we would like to use it to predict
% the labels. You will now implement the "predict" function to use the
% neural network to predict the labels of the training set. This lets
% you compute the training set accuracy.
pred = predict(Theta1, Theta2, X);
fprintf('\nTraining Set Accuracy: %f\n', mean(double(pred == y)) * 100);
fprintf('Part 3 Program paused. Press enter to continue.\n');
pause;
% To give you an idea of the network's output, you can also run
% through the examples one at the a time to see what it is predicting.
% Randomly permute examples
rp = randperm(m);
for i = 1:m
% Display
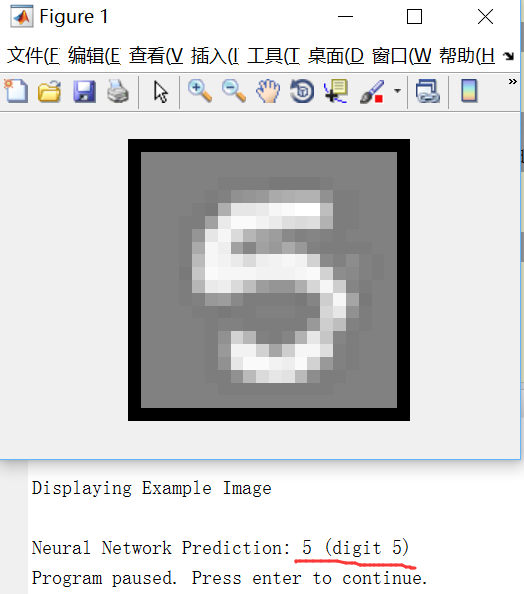
fprintf('\nDisplaying Example Image\n');
displayData(X(rp(i), :));
pred = predict(Theta1, Theta2, X(rp(i),:));
fprintf('\nNeural Network Prediction: %d (digit %d)\n', pred, mod(pred, 10));
% Pause
fprintf('Program paused. Press enter to continue.\n');
pause;
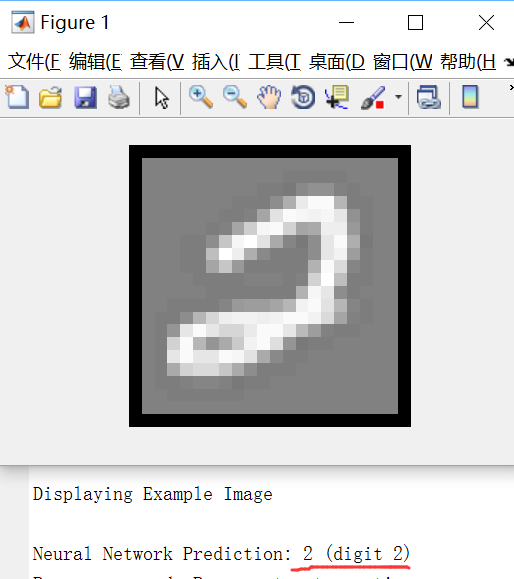
end執行效果如下:
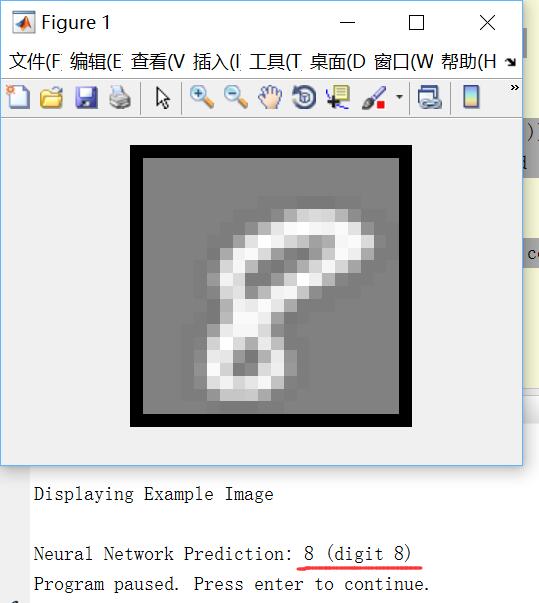
很好玩吧!這就是一個比較完備的手寫數字識別器了。
四、總結
以上建立的神經網路的權重引數都是已經給好的。那麼這些引數是如何得到的呢?下一篇博文會介紹學習這些權重引數的演算法。